Zmienna lingwistyczna

Relacje rozmyte
Relacją rozmytą R między dwoma zbiorami (nierozmytymi) X i Y nazywamy zbiór rozmyty określony na iloczynie kartezjańskim X × Y . Relacja rozmyta jest zbiorem par:
gdzie μR : X × Y → [0, 1] jest funkcją przynależności.
Funkcja ta każdej parze (x; y), x ∈ X, y ∈ Y przypisuje stopień przynależności μR (x; y), który ma interpretację siły powiązania między elementami x ∈ X i y ∈ Y .

Relacje rozmyte
Przykład:
Określmy przestrzenie rozważań: X = {x1; x2; x3} = {3; 4; 5}, Y = {y1; y2; y3} = {4; 5; 6} oraz relację R ⊂ X×Y jako "y jest mniej więcej równe x". Relację tę można zdefiniować:
lub jako macierz [aij ], gdzie wartość aij oznacza stopień powiązania między elementami xi i yj :

Relacje rozmyte
Przykład:
Zatem funkcja przynależności ma postać:
jeżeli x=y
jeżeli |x-y|=1
jeżeli |x-y|=2
jeżeli |x-y|=3

Wnioskowanie w logice dwuwartościowej
Reguła modus ponens
Przykład:
A ma postać: „Jan jest kierowcą”, B ma postać „Jan ma prawo jazdy”. Jeżeli A=1, to B=1, gdyż z prawdziwości faktu oraz reguły wynika prawdziwość wniosku.
Czyli jeśli „Jan jest kierowcą” to „Jan ma prawo jazdy”.

Wnioskowanie w logice dwuwartościowej
Reguła modus tollens
Przykład:
Nie A ma postać: „Jan nie jest kierowcą”, nie B ma postać „Jan nie ma prawa jazdy”. Jeżeli B=0 (nie B=1), to A=0 (nie A=1), gdyż z prawdziwości faktu oraz reguły wynika prawdziwość wniosku.
Czyli jeśli „Jan nie ma prawa jazdy” to „Jan nie jest kierowcą”.

Wnioskowanie w logice rozmytej
Rozmyta reguła modus ponens
A, A’ ⊆ X oraz B, B’ ⊆ Y są zbiorami rozmytymi
x, y są zmiennymi lingwistycznymi
Reguła jest relacją rozmytą.

Wnioskowanie w logice rozmytej
Rozmyta reguła modus ponens - przykład
Przesłanki oraz wniosek są nieprecyzyjnymi stwierdzeniami. Zmienne lingwistyczne: x – prędkość samochodu, y – poziom hałasu.
Zbiór
T1={„mała”, „średnia”, „duża”, „bardzo duża”}
jest zbiorem wartości zmiennej lingwistycznej x.
Zbiór
T2={„mały”, „średni”, „średnio wysoki”, „wysoki”}
jest zbiorem wartości zmiennej lingwistycznej y.

Wnioskowanie w logice rozmytej
Rozmyta reguła modus ponens - przykład
Do każdego elementu zbioru T1 i T2 można przyporządkować odpowiedni zbiór rozmyty. W tym przypadku:
A=„bardzo duża prędkość samochodu”
A’=„duża prędkość samochodu”
B=„wysoki poziom hałasu”
B’=„średnio wysoki poziom hałasu”

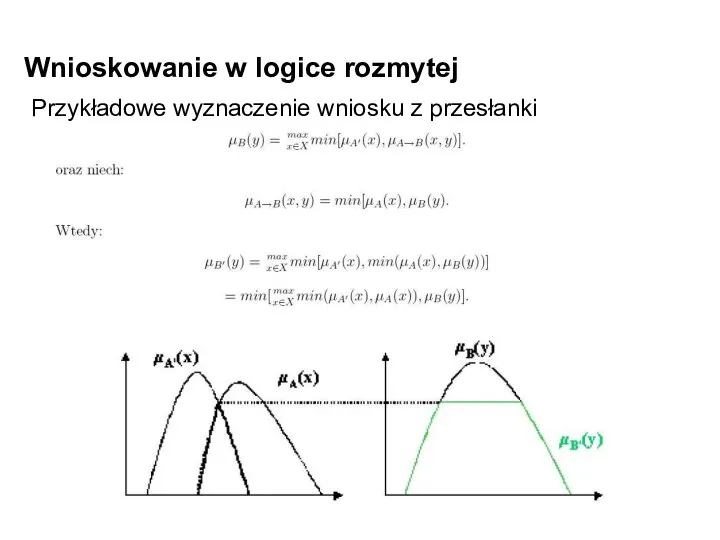
Wnioskowanie w logice rozmytej
Przykładowe wyznaczenie wniosku z przesłanki

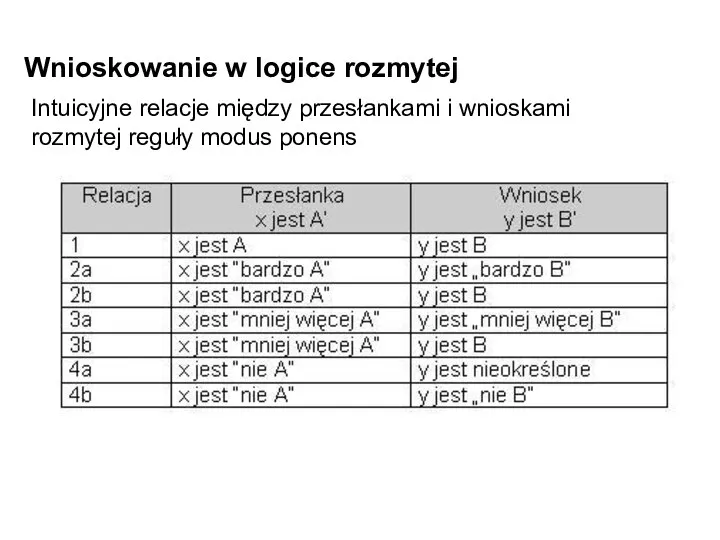
Wnioskowanie w logice rozmytej
Intuicyjne relacje między przesłankami i wnioskami rozmytej reguły modus ponens

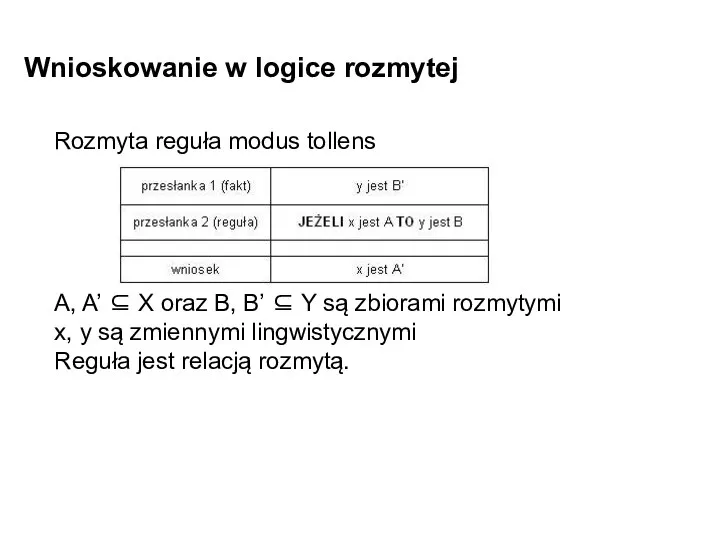
Wnioskowanie w logice rozmytej
Rozmyta reguła modus tollens
A, A’ ⊆ X oraz B, B’ ⊆ Y są zbiorami rozmytymi
x, y są zmiennymi lingwistycznymi
Reguła jest relacją rozmytą.

Wnioskowanie w logice rozmytej
Rozmyta reguła modus tollens - przykład
Przesłanki oraz wniosek są nieprecyzyjnymi stwierdzeniami. Zmienne lingwistyczne: x – prędkość samochodu, y – poziom hałasu.
Zbiór
T1={„mała”, „średnia”, „duża”, „bardzo duża”}
jest zbiorem wartości zmiennej lingwistycznej x.
Zbiór
T2={„mały”, „średni”, „średnio wysoki”, „wysoki”}
jest zbiorem wartości zmiennej lingwistycznej y.

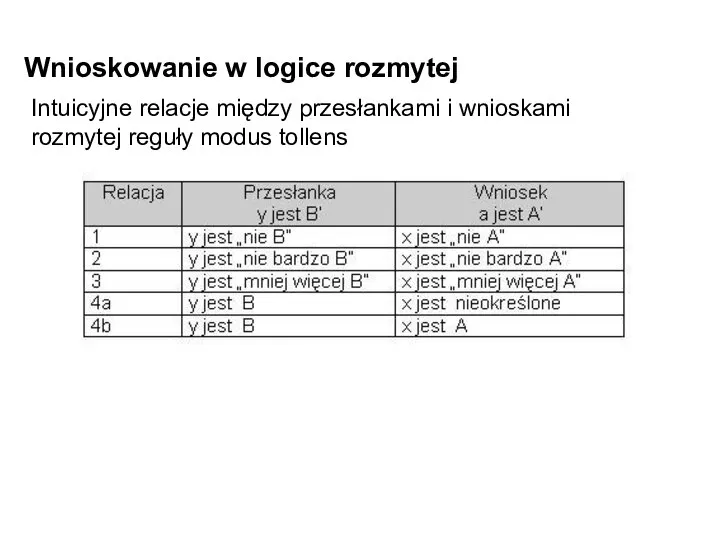
Wnioskowanie w logice rozmytej
Intuicyjne relacje między przesłankami i wnioskami rozmytej reguły modus tollens

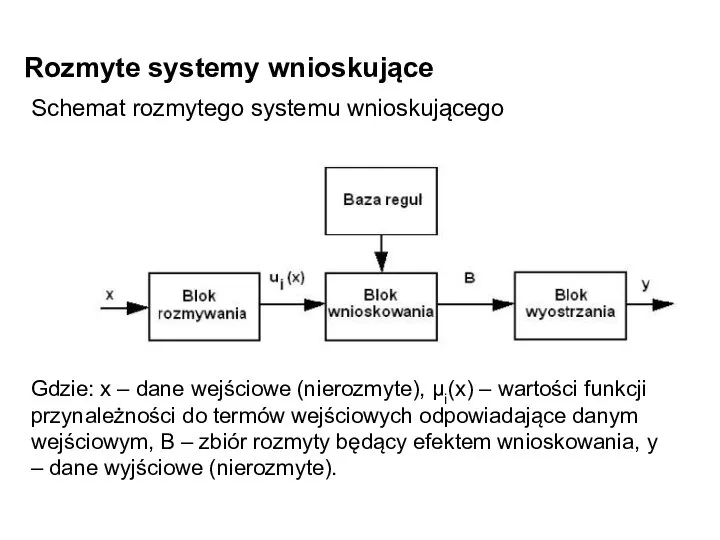
Rozmyte systemy wnioskujące
Schemat rozmytego systemu wnioskującego
Gdzie: x – dane wejściowe (nierozmyte), μi(x) – wartości funkcji przynależności do termów wejściowych odpowiadające danym wejściowym, B – zbiór rozmyty będący efektem wnioskowania, y – dane wyjściowe (nierozmyte).

Rozmyte systemy wnioskujące
Blok rozmywania
Konkretna wartość podana na wejście systemu rozmytego podlega operacji rozmywania. Po rozmyciu wartość wejściowa zostaje odwzorowana w zbiór rozmyty.
Przykład operacji rozmywania.

Rozmyte systemy wnioskujące
Baza reguł
W bazie reguł przechowywana jest wiedza dotycząca rozważanego problemu. Reguły zapisywane są w formie wyrażeń JEŻELI... TO...
Przy projektowaniu systemów rozmytych należy rozstrzygnąć czy:
liczba reguł jest wystarczająca
reguły nie są sprzeczne
zachodzą interakcje pomiędzy poszczególnymi regułami
Prosta baza reguł może wyglądać następująco:
R1: Jeżeli temperatura = niska To ogrzewanie = duże
R2: Jeżeli temperatura = średnia To ogrzewanie = średnie
R3: Jeżeli temperatura = wysoka To ogrzewanie = niskie

Rozmyte systemy wnioskujące
Blok wnioskowania
Na wejściu bloku wnioskowania pojawia się rozmyta wartość wejściowa. Na wyjściu tego bloku pojawia się zbiór rozmyty powstały w wyniku wnioskowania. Wnioskowanie przeprowadza się na podstawie reguł zawartych w bazie reguł.

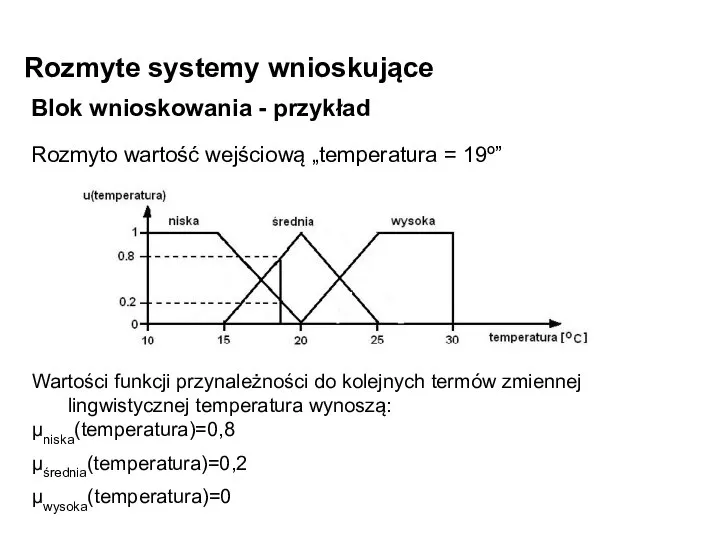
Rozmyte systemy wnioskujące
Blok wnioskowania - przykład
Rozmyto wartość wejściową „temperatura = 19º”
Wartości funkcji przynależności do kolejnych termów zmiennej lingwistycznej temperatura wynoszą:
μniska(temperatura)=0,8
μśrednia(temperatura)=0,2
μwysoka(temperatura)=0

Rozmyte systemy wnioskujące
Blok wnioskowania - przykład
W bazie reguł znajdują się następujące reguły, które mogą być wykorzystane do wnioskowania:
R1: Jeżeli temperatura = niska To ogrzewanie = duże
R2: Jeżeli temperatura = średnia To ogrzewanie = średnie
Proces uruchomienia reguł R1 i R2

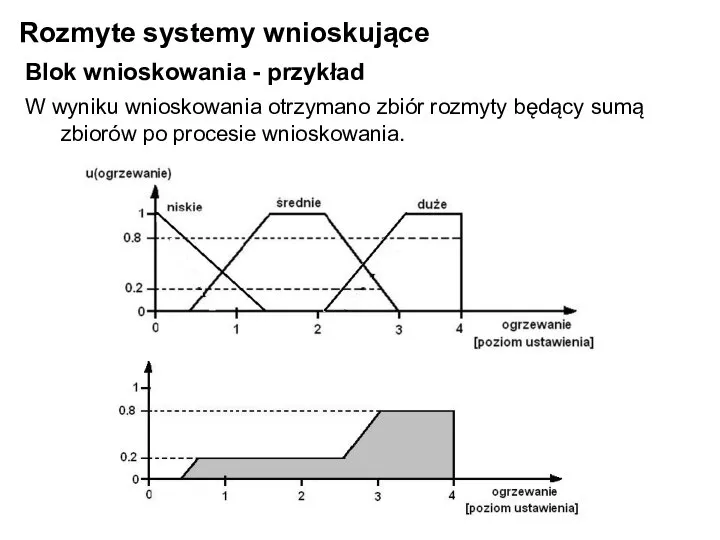
Rozmyte systemy wnioskujące
Blok wnioskowania - przykład
W wyniku wnioskowania otrzymano zbiór rozmyty będący sumą zbiorów po procesie wnioskowania.

Rozmyte systemy wnioskujące
Blok wyostrzania
Wielkością wyjściową bloku wnioskowania jest N zbiorów rozmytych Bi z funkcjami przynależności μBi(y), i=1,2,...,N lub jeden zbiór rozmyty B’ z funkcją przynależności μB’(y).
Należy odwzorować zbiory rozmyte Bi w jedną wartość y∈Y. Wartość y jest odpowiedzą systemu rozmytego na podaną na jego wejście wartość x∈X.
Odwzorowanie to nazywa się wyostrzaniem.
Najbardziej popularna metoda wyostrzania to metoda środka ciężkości. y wyznacza się z zależności:
gdzie yk jest punktem, w którym funkcja μB(y) osiąga maksimum.

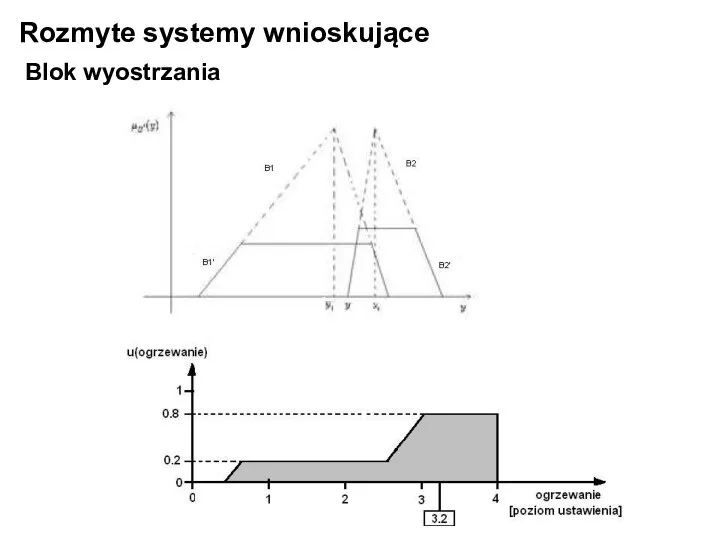
Rozmyte systemy wnioskujące
Blok wyostrzania

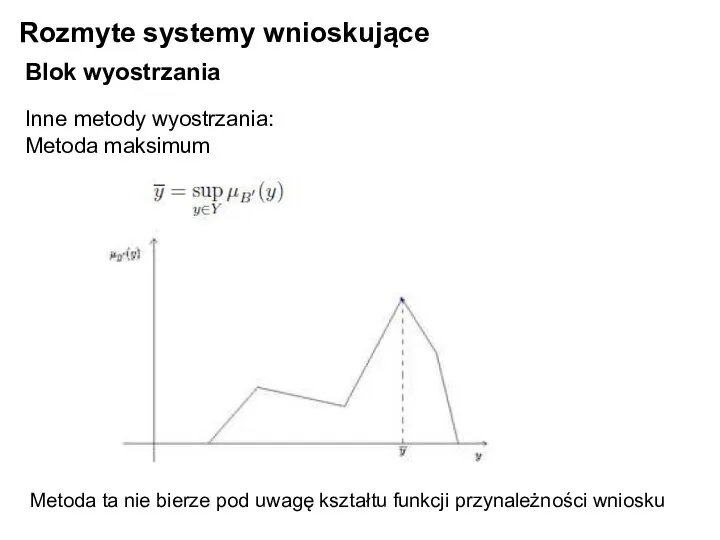
Rozmyte systemy wnioskujące
Blok wyostrzania
Inne metody wyostrzania:
Metoda maksimum
Metoda ta nie bierze pod uwagę kształtu funkcji przynależności wniosku

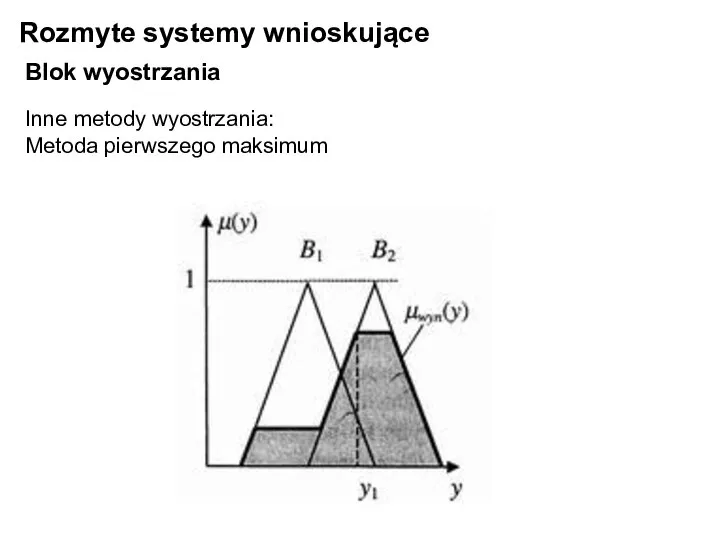
Rozmyte systemy wnioskujące
Blok wyostrzania
Inne metody wyostrzania:
Metoda pierwszego maksimum