Знакомьтесь, уравнение

Знакомьтесь, уравнение!
Работу выполнила
ученица 9-го класса
Лёвина Дарья

Определение квадратного уравнения
называется квадратным уравнением
где х – переменная,
а, b и c – некоторые числа,
причем а ≠ 0
Уравнение вида
МОУ
Тулиновская средняя общеобразовательная школа

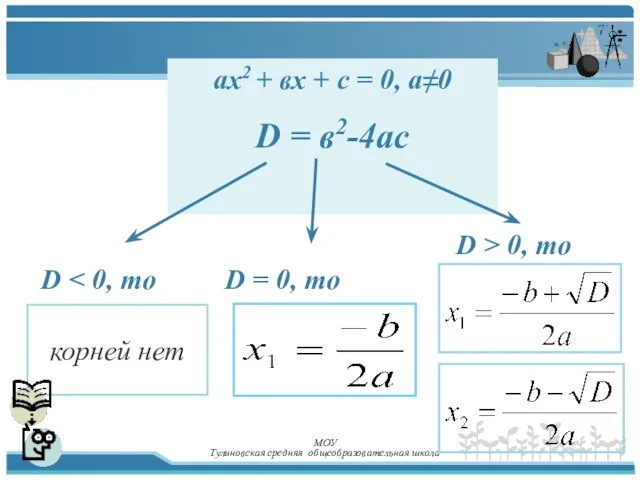
МОУ
Тулиновская средняя общеобразовательная школа
называется дискриминантом
Выражение

МОУ
Тулиновская средняя общеобразовательная школа
aх2 + вх + с = 0, а≠0
D = в2-4ас
D < 0, то
D = 0, то
D > 0, то
корней нет

Исторические сведения
Необходимость решать уравнения не только первой, но и второй степени в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и работами военного характера, с развитием астрономии и математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне.
Web - Web - сайт
МОУ
Тулиновская средняя общеобразовательная школа

Цель исследования:
Выяснить, можно ли решать квадратное уравнение с помощью циркуля и линейки
МОУ
Тулиновская средняя общеобразовательная школа

Гипотеза
По данным действительным коэффициентам a, b, c уравнения
ax2 + bx + c = 0 (a ≠ 0) можно определить радиус и координаты центра окружности, пересекающей ось Ox в точках, абсциссы которых являются корнями данного уравнения
МОУ
Тулиновская средняя общеобразовательная школа

Ход исследования:
1. Изучив теоретический материал учебника и дополнительных источников информации выяснить, способы решения квадратных уравнений с помощью циркуля и линейки.
2. Изучить историю квадратных уравнений.
3. Оформить результаты, сделать соответствующие выводы.
МОУ
Тулиновская средняя общеобразовательная школа

Задача.
По данным действительным коэффициентам a, b, c уравнения
ax2 + bx + c = 0 (a ≠ 0) определить радиус и координаты центра окружности, пересекающей ось Ox в точках, абсциссы которых являются корнями данного уравнения .
МОУ
Тулиновская средняя общеобразовательная школа

Ход решения задачи
у
х
(х1;0)
(х2;0)
F
B
K
E
A
O
C
(0;1)
S
(
;
)
(0;
)
МОУ
Тулиновская средняя общеобразовательная школа

План нахождения корней квадратного уравнения с помощью циркуля и линейки
В системе координат построим
точки и А (0;1).
Проведём окружность с радиусом SA.
3. Абсциссы точек пересечения окружности с осью Ох являются корнями исходного квадратного уравнения.
МОУ
Тулиновская средняя общеобразовательная школа

у
х
(х1;0)
K
E
A
O
(0;1)
S
(0;
)
Радиус окружности больше ординаты центра
В этом случае окружность пересекает ось Ох в точках В(х1;0) С(х2;0)
(х2;0)
С
В
МОУ
Тулиновская средняя общеобразовательная школа

у
х
(х1;0)
E
A
O
(0;1)
S
(0;
)
Радиус окружности равен ординате центра
В этом случае уравнение имеет равные действительные корни, абсцисса точки касания х1,2 =
В
МОУ
Тулиновская средняя общеобразовательная школа

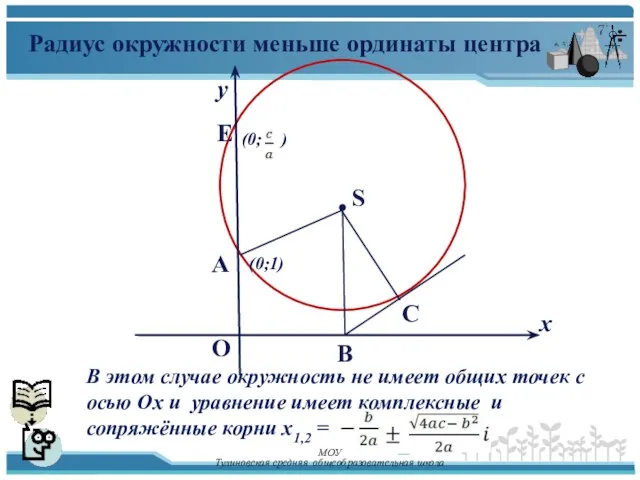
у
х
E
A
O
(0;1)
S
(0;
)
Радиус окружности меньше ординаты центра
В этом случае окружность не имеет общих точек с осью Ох и уравнение имеет комплексные и сопряжённые корни х1,2 =
=
В
С
МОУ
Тулиновская средняя общеобразовательная школа

Примеры:
а) 2x2 + 3x + 1 = 0
Определим координаты точки центра окружности по формулам:
x =
y =
Проведём окружность радиуса SA, где А(0;1). Корни уравнения -1 и - 0,5.
О
у
х
А
-0,5
S
-1
1
МОУ
Тулиновская средняя общеобразовательная школа

Примеры:
б) x2 - 5x + 6 = 0
Определим координаты точки центра окружности по формулам:
x =
y =
Проведём окружность радиуса SA, где А(0;1). Корни уравнения 2 и 3.
О
у
х
А
3
1
2
МОУ
Тулиновская средняя общеобразовательная школа

Выводы
1. Квадратные уравнения можно решать с помощью циркуля и линейки.
2. По данным действительным коэффициентам a, b, c уравнения
ax2 + bx + c = 0 (a ≠ 0) можно определить радиус и координаты центра окружности, пересекающей ось Ox в точках, абсциссы которых являются корнями данного уравнения
МОУ
Тулиновская средняя общеобразовательная школа

Способы решения квадратных уравнений
Изучаемые в школе:
Разложение левой части на множители Метод выделения полного квадрата
С применением формул корней квадратного уравнения
С применением теоремы Виета
Графический способ
МОУ
Тулиновская средняя общеобразовательная школа

Способы решения квадратных уравнений
Продвинутые способы:
Способ переброски
По свойству коэффициентов
С помощью циркуля и линейки
С помощью номограммы
Геометрический
МОУ
Тулиновская средняя общеобразовательная школа