Содержание
- 2. Немного истории… Одним из важнейших этапов в развитии понятия о числе было введение отрицательных чисел -
- 3. Еще немного…. В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни
- 4. Математики Итальянский алгебраист Дж. Кардано1545 г. предложил ввести числа новой природы. Он показал, что система уравнений
- 5. Кардано называл такие величины "чисто отрицательными" и даже "софистически отрицательными", считал их бесполезными и старался их
- 6. Уже в 1572 году вышла книга итальянского алгебраиста Р. Бомбелли, в которой были установлены первые правила
- 7. Название "мнимые числа" ввел в 1637 году французский математик и философ Р. Декарт, а в 1777
- 8. В 1637 году вышел в свет главный математический труд Декарта, «Рассуждение о методе» (полное название: «Рассуждение
- 9. Этот символ(i) вошел во всеобщее употребление благодаря К. Гауссу. Термин "комплексные числа" так же был введен
- 10. Уже в двухлетнем возрасте Гаусс показал себя вундеркиндом. В три года он умел читать и писать,
- 11. Постепенно развивалась техника операций над мнимыми числами. На рубеже XVII и XVIII веков была построена общая
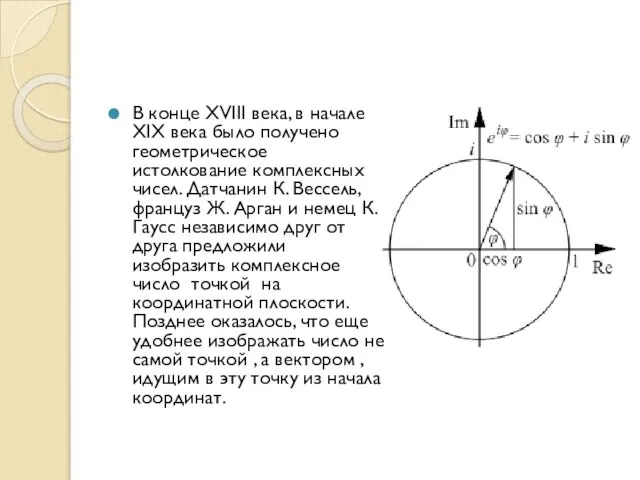
- 12. Л. Эйлер вывел в 1748 году замечательную формулу: которая связывала воедино показательную функцию с тригонометрической. С
- 13. Эйлер оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных
- 14. В конце XVIII века, в начале XIX века было получено геометрическое истолкование комплексных чисел. Датчанин К.
- 15. После создания теории комплексных чисел возник вопрос о существовании "гиперкомплексных" чисел - чисел с несколькими "мнимыми"
- 16. Список используемой литературы: Сайт «Wikipedia» "Энциклопедический словарь юного математика"
- 18. Скачать презентацию














 Пермский край: инвестиционные возможности
Пермский край: инвестиционные возможности Системные платы Gigabyte
Системные платы Gigabyte Кроссворд на английском языке
Кроссворд на английском языке Проектирование системы электроснабжения электроаппаратного завода
Проектирование системы электроснабжения электроаппаратного завода Древние образы народного искусства
Древние образы народного искусства Решение квадратных уравнений
Решение квадратных уравнений Антимонопольное регулирование в авторитейле
Антимонопольное регулирование в авторитейле Завтрак чемпиона от Широковой Полины. Омлет с сыром, молоко
Завтрак чемпиона от Широковой Полины. Омлет с сыром, молоко Highlights of sports
Highlights of sports Просвещенный абсолютизм в России
Просвещенный абсолютизм в России Феофан Грек, Андрей Рублев
Феофан Грек, Андрей Рублев "Платон" - Философия
"Платон" - Философия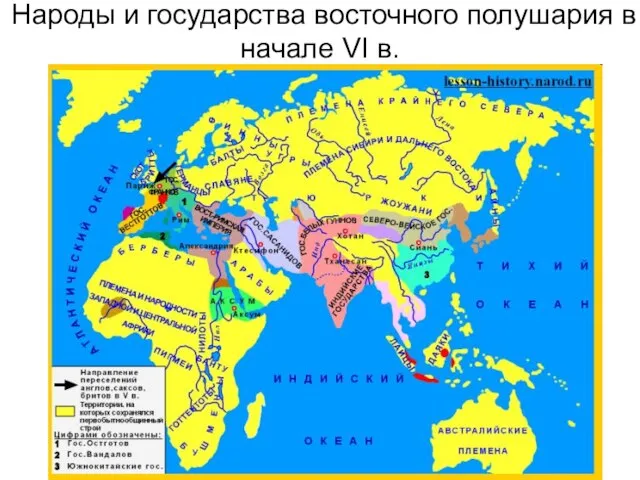 Народы и государства восточного полушария в начале VI в.
Народы и государства восточного полушария в начале VI в. Деятельность
Деятельность ЖИЗНЬ КЛАССА 1 сентября Посвящение в гимназисты Хореография Экскурсия в Автогородок Новогодний калейдоскоп Масленица Наша пл
ЖИЗНЬ КЛАССА 1 сентября Посвящение в гимназисты Хореография Экскурсия в Автогородок Новогодний калейдоскоп Масленица Наша пл ОРГАНИЗАЦИЯ ПЕРЕВОЗКИ ВНЕШНЕТОРГОВЫХ ГРУЗОВ АВТОМОБИЛЬНЫМ ТРАНСПОРТОМ Преподаватель: доцент кафедры МЭО, к.э.н., Журова А.В.
ОРГАНИЗАЦИЯ ПЕРЕВОЗКИ ВНЕШНЕТОРГОВЫХ ГРУЗОВ АВТОМОБИЛЬНЫМ ТРАНСПОРТОМ Преподаватель: доцент кафедры МЭО, к.э.н., Журова А.В. Участники "Первого Дома на Родине" отмечают свою первую Хануку в Израиле
Участники "Первого Дома на Родине" отмечают свою первую Хануку в Израиле Реклама и маркетинг
Реклама и маркетинг Изображение цветка пиона в разных техниках художественной обработки
Изображение цветка пиона в разных техниках художественной обработки Мутационная изменчивость 10 класс
Мутационная изменчивость 10 класс Byredo Blanche. Парфюмерия
Byredo Blanche. Парфюмерия Элетромеханический замок с убегающим кодом
Элетромеханический замок с убегающим кодом Особенности формирования требований информационной безопасности Реестра источников ионизирующего излучения (ИИИ), которые могут
Особенности формирования требований информационной безопасности Реестра источников ионизирующего излучения (ИИИ), которые могут Valentine game
Valentine game Аспартам
Аспартам Попечительский совет или Управляющий совет?
Попечительский совет или Управляющий совет? Компания Декорсталь – Производитель декоративных сталей
Компания Декорсталь – Производитель декоративных сталей Taller de comunicación oral y escrita
Taller de comunicación oral y escrita