Содержание
- 2. Милетская школа: проблема единого первоначала Проблема единства сущего Проблема первоначала (архе) Фалес: вода как первоначало сущего
- 3. Милетская школа Проблема единого первоначала Милет
- 4. Милетская школа Проблема единого первоначала Фалес (ок. 640-562) Анаксимандр (ок. 610-ок. 540) Анаксимен (ок. 588-ок. 525)
- 5. Милетская школа Проблема единства сущего Взаимопревращения веществ свидетельствуют, что за видимым многообразием воспринимаемого мира скрывается единое
- 6. Милетская школа Проблема первоначала (архе) Архé (греч. αρχή, лат. principium) – термин древнегреческой философии, означающий начало
- 7. Милетская школа Проблема первоначала (архе) Аристотель. «Метафизика». ... большинство первых философов считало началом то, из чего
- 8. Фалес Вода как первоначало Аристотель. «Метафизика». Относительно количества и вида такого начала не все учили одинаково.
- 9. Милетская школа Проблема первоначала (архе) Философ Первоначало Фалес Вода Анаксимандр Апейрон (беспредельное, неопределённое) Анаксимен Воздух
- 10. Анаксимандр Апейрон как первоначало Áпейрон (греч. άπειρον; от α, отрицательная приставка, и πέρας, конец, предел) –
- 11. Анаксимандр Апейрон как первоначало Диоген Лаэртский. «О жизни, учениях и изречениях знаменитых философов». Анаксимандр Милетский... учил,
- 12. Анаксимен Воздух как первоначало Ипполит. «Опровержение всех ересей». Анаксимен... полагал, что начало – бесконечный воздух, из
- 13. Гераклит Проблема изменчивости Милет Эфес
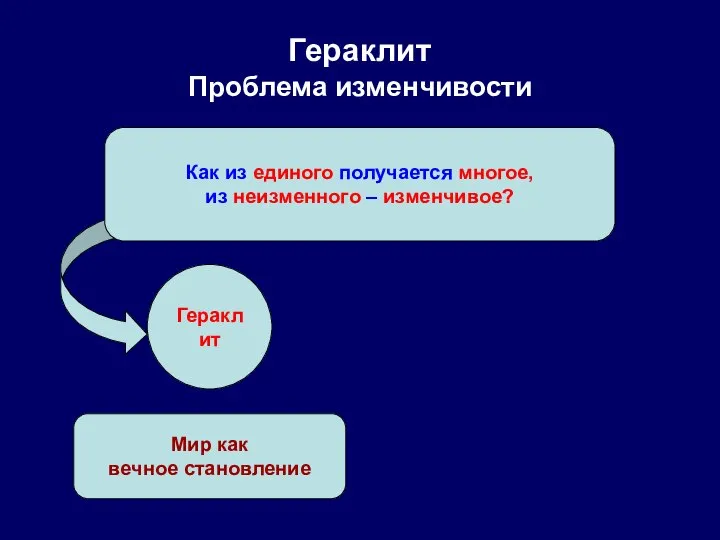
- 14. Гераклит Проблема изменчивости Как из единого получается многое, из неизменного – изменчивое? Гераклит Мир как вечное
- 15. Гераклит Мир как вечное становление (генезис) Гераклит (ок. 540 - 480) Этот космос, тот же самый
- 16. Гераклит Мир как вечное становление (генезис) Первоначало по природе своей изменчиво: стихия мира – огонь. Мир
- 17. Элейская школа Иллюзорность изменчивости Милет Эфес Элея
- 18. Элейская школа Иллюзорность изменчивости Парменид (род. 540/539) Зенон (ок. 490 - 430)
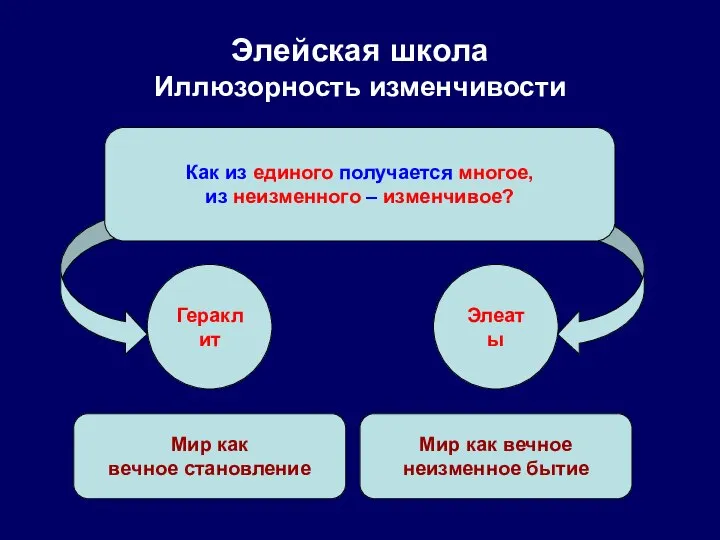
- 19. Элейская школа Иллюзорность изменчивости Как из единого получается многое, из неизменного – изменчивое? Элеаты Мир как
- 20. Парменид Мир как единое, вечное и неизменное бытие Бытие есть, небытия нет Бытие едино и неделимо
- 21. Парменид Мир как единое, вечное и неизменное бытие Рассел. «История западной философии». Часто говорят, что Парменид
- 22. Парадоксы Зенона Обоснование элейской онтологии Апория места (немыслимость пустоты) Апории множества (немыслимость множества) Парадокс делимости Парадокс
- 23. Парадоксы Зенона Обоснование элейской онтологии Апорúя (греч. απορία, затруднение, безвыходное положение; от α, отрицательная приставка, и
- 24. Парадоксы Зенона Апория места Если условием существования является нахождение в каком-то месте, то и само место,
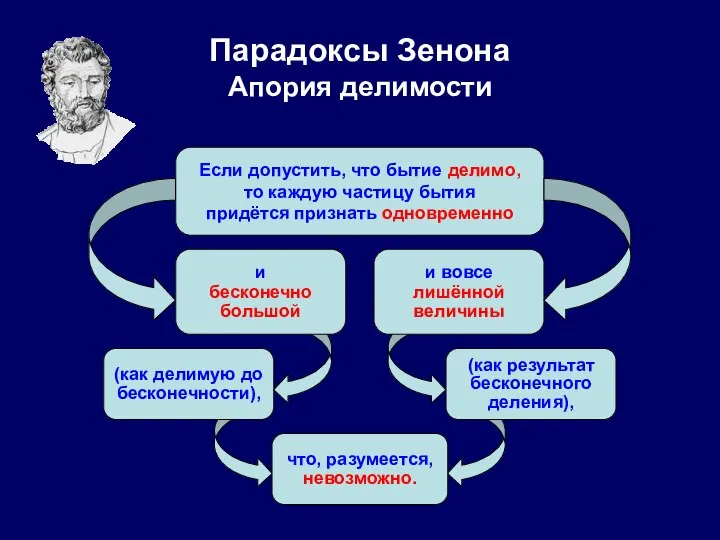
- 25. Парадоксы Зенона Апория делимости Если допустить, что бытие делимо, то каждую частицу бытия придётся признать одновременно
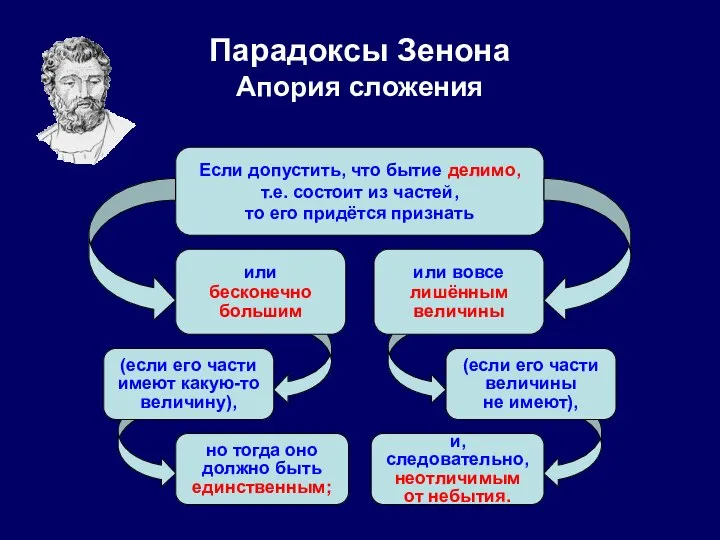
- 26. Парадоксы Зенона Апория сложения Если допустить, что бытие делимо, т.е. состоит из частей, то его придётся
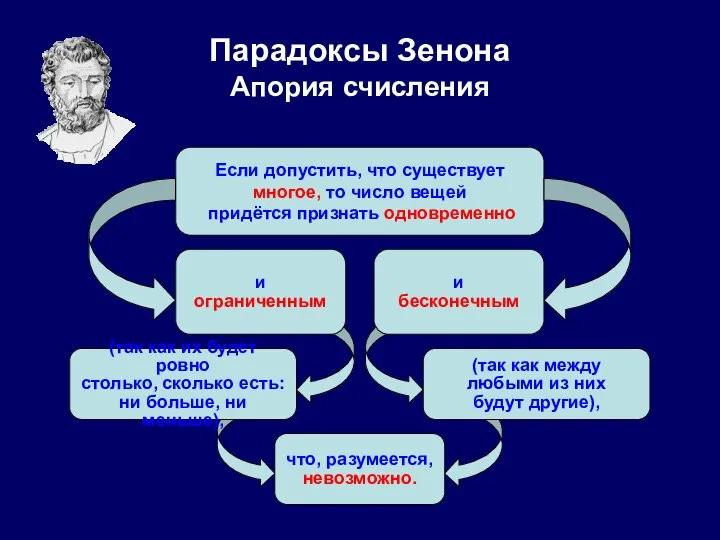
- 27. Парадоксы Зенона Апория счисления Если допустить, что существует многое, то число вещей придётся признать одновременно и
- 28. Парадоксы Зенона Апория «Ахилл и черепаха» Быстроногий Ахилл никогда не догонит медленно ползущую черепаху, так как
- 29. Парадоксы Зенона Апория «Ахилл и черепаха»
- 30. Парадоксы Зенона Апория «Ахилл и черепаха»
- 31. Парадоксы Зенона Апория «Дихотомия» Дuхотомúя (греч. διχοτομία; от δίχα, на две части, и τομή, сечение, разделение)
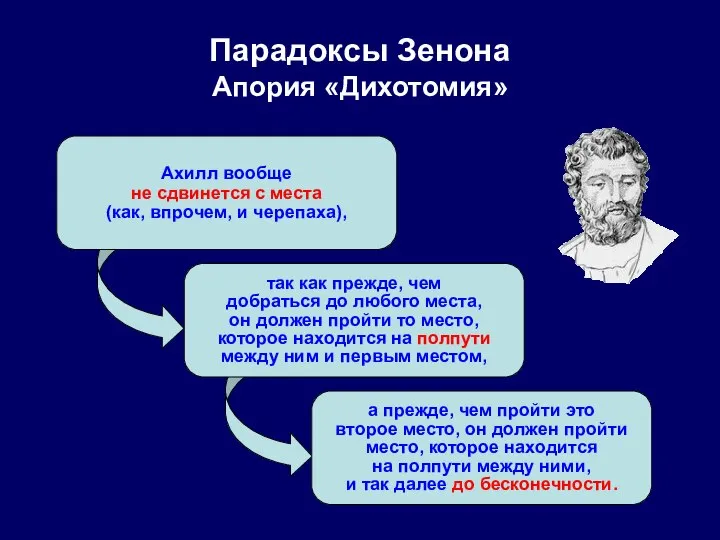
- 32. Парадоксы Зенона Апория «Дихотомия» Ахилл вообще не сдвинется с места (как, впрочем, и черепаха), а прежде,
- 33. Парадоксы Зенона Апория «Дихотомия»
- 34. Парадоксы Зенона Апории движения Первые две апории демонстрируют немыслимость движения при допущении бесконечной делимости времени и
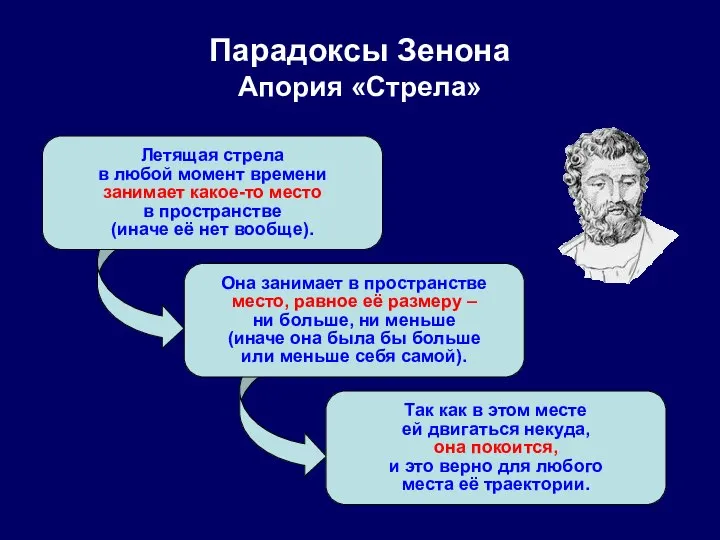
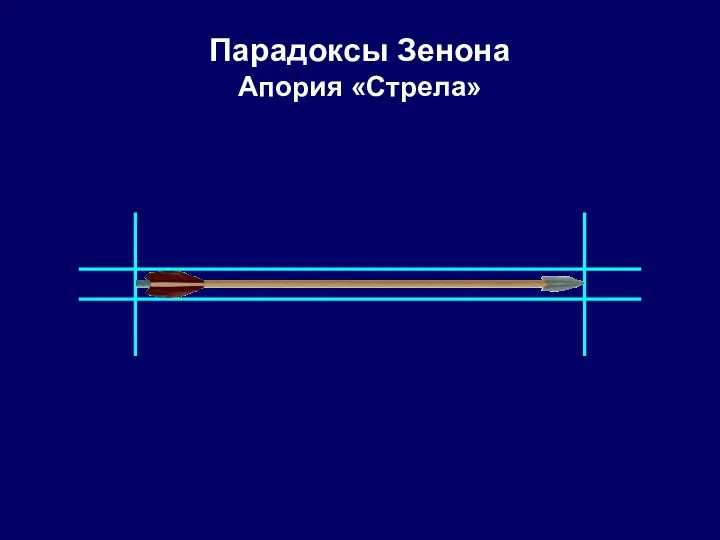
- 35. Парадоксы Зенона Апория «Стрела» Летящая стрела в любой момент времени занимает какое-то место в пространстве (иначе
- 36. Парадоксы Зенона Апория «Стрела»
- 37. Таким образом, получится, что минимальная, т.е. неделимая, единица времени делима, что абсурдно. (Равным образом, делимой окажется
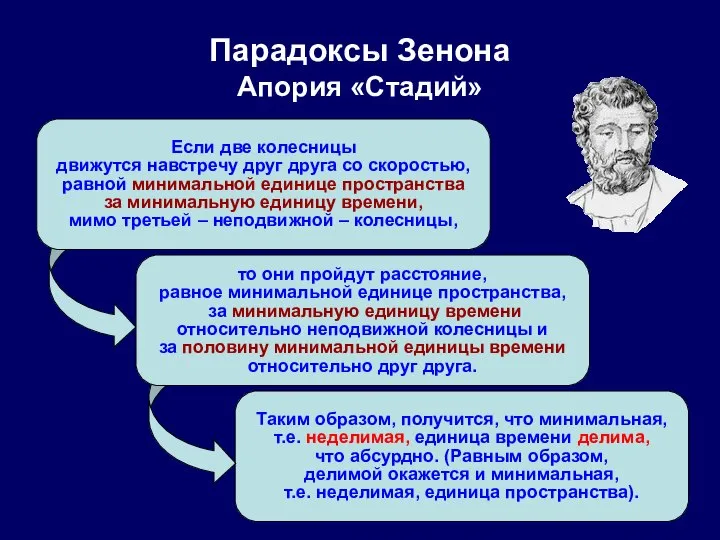
- 38. Парадоксы Зенона Апория «Стадий»
- 40. Скачать презентацию

























 Prezentatsia_4
Prezentatsia_4 Постпозитивизм К. Поппер, Т. Кун, И. Лакатос
Постпозитивизм К. Поппер, Т. Кун, И. Лакатос Природа и общество как важнейшие проблемы социальной философии и ее основной вопрос
Природа и общество как важнейшие проблемы социальной философии и ее основной вопрос Философия. Круг ее проблем и роль в обществе
Философия. Круг ее проблем и роль в обществе Становление и истоки формирования казахской философии
Становление и истоки формирования казахской философии Инфографика, как способ передачи мысли
Инфографика, как способ передачи мысли Презентация история и методология юридической науки
Презентация история и методология юридической науки Традиционная культура в современном обществе
Традиционная культура в современном обществе Интеллектуальная игра по дисциплине «Философия» Подготовили студентки 1-ого курса ФТД Группы Т-116 Федина Юля и Цьопа Даша
Интеллектуальная игра по дисциплине «Философия» Подготовили студентки 1-ого курса ФТД Группы Т-116 Федина Юля и Цьопа Даша Технологии мышления
Технологии мышления Учение о человеке
Учение о человеке Отечественная философия и ее особенности. Лекция 4
Отечественная философия и ее особенности. Лекция 4 Образ человека в православной культуре России
Образ человека в православной культуре России Античная философия
Античная философия Технология мышления
Технология мышления Философско-правовые идеи Никколо Макиавелли
Философско-правовые идеи Никколо Макиавелли Современные направления философии конца IX века – начала XX века
Современные направления философии конца IX века – начала XX века Философия в системе культуры (ПР№20)
Философия в системе культуры (ПР№20) Миссия школы как управленческая инновация
Миссия школы как управленческая инновация Античная философия
Античная философия Философский дискурс о модерне
Философский дискурс о модерне Человек и отчуждение. Возрождение диалектического метода исследования
Человек и отчуждение. Возрождение диалектического метода исследования Даосизм. Джайнизм (VI-V вв. до н. э.)
Даосизм. Джайнизм (VI-V вв. до н. э.) Науки о природе
Науки о природе История философии. Этап I. Древний мир
История философии. Этап I. Древний мир Предфилософские формы мировоззрения
Предфилософские формы мировоззрения Эллинистическая философия. Эпикурейцы и стоики
Эллинистическая философия. Эпикурейцы и стоики Теология - мировоззренческая угроза
Теология - мировоззренческая угроза