Логика. Силлогизмы. Круги Эйлера

Понятие логики
Логика – наука о доказательствах, аргументах, на основании которых делаются умозаключения.
Доказательство – это рациональный логический переход от принятой точки зрения (предпосылки) к тому пункту, где её следует обосновать (вывод).
Предпосылки – это основные положения, которые должны быть приняты для осуществления доказательства.
Переход от предпосылки к выводу осуществляется с помощью умозаключения.
Одна из задач логики – отличать истинность и ложность умозаключений.

Классическая логика
Классическая логика создана Аристотелем.
Она не изменялась существенно до конца 19 века.
В основе классической логики лежит понятие «силлогизма».
Силлогизм – это умозаключение, основанное на трёх суждениях (две посылки и вывод).
Силлогизм от Аристотеля:
Все люди смертны (P есть S);
Греки – люди (Q есть P);
Следовательно, греки смертны.(Q есть S).

Составить силлогизмы
?;
Малиновка – птица;
Малиновка покрыта перьями.
2. Все рыбы имеют жабры;
?;
Окунь имеет жабры.
Планеты Солнечной системы вращаются вокруг Солнца;
Венера - планета Солнечной системы;
?.

Фигуры силлогизмов
Фигура 1
Все большие посылки общие
Все меньшие посылки утвердительны.
(Классические примеры силлогизмов с предыдущего слайда)

Фигуры силлогизмов
Фигура 2
Все большие посылки общие;
Все заключения отрицательны;
Одна посылка всегда отрицательна.
Пример:
Кислород поддерживает горение (P есть S)
Этот газ не поддерживает горения (Q не есть S)
Этот газ не есть кислород (Q не есть P)

Фигуры силлогизмов
Фигура 3
Все меньшие посылки утвердительны;
Все заключения частные.
Все киты суть млекопитающие (P есть S)
Все киты живут в воде (P есть Q)
Некоторые живущие в воде животные суть млекопитающие (Q есть S)

Фигуры силлогизмов
Фигура 4
Cредний термин взят сказуемым в большей и подлежащим в меньшей посылке. Сказуемое в меньшей посылке взято не во всём объёме, поэтому и в заключении оно должно быть взято не во всём объёме.
Пример
Все металлы суть материальные вещи (P есть Q)
Все материальные вещи имеют тяжесть (Q есть S)
Некоторые тела, имеющие тяжесть, суть металлы
(S есть P)

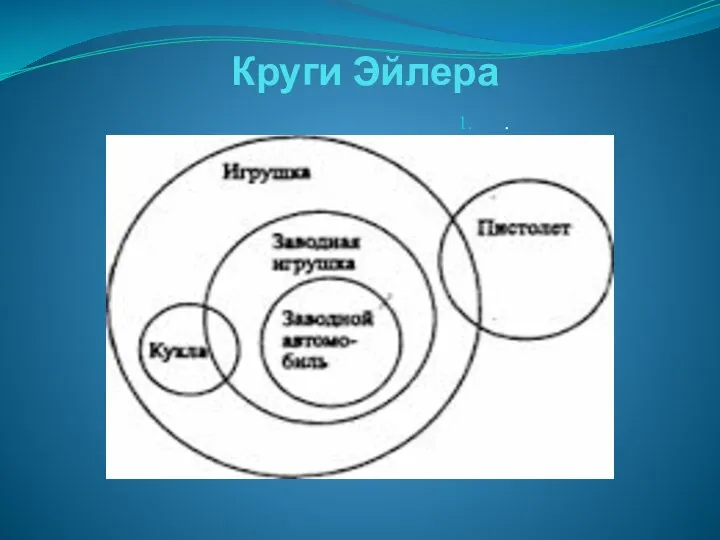
Круги Эйлера
Круги Эйлера – это геометрическая наглядная иллюстрация объёмов понятий и отношений между ними с помощью кругов.
Пример: Если круг A иллюстрирует объем понятия «студенты», а круг В иллюстрирует объем понятия «спортсмены», то отношение между объемами этих понятий можно изображать в виде двух пересекающихся кругов . Заштрихованная общая площадь кру­га A и круга В будет обозначать объем студентов, являющихся одновременно спортсменами.

Круги Эйлера

Круги Эйлера
.

Вопросы на сообразительность
Что принадлежит вам, однако другие им пользуются чаще, чем вы?
Сидит человек, но вы не можете сесть на его место, даже если он встанет и уйдёт. Где он сидит?
Может ли петух назвать себя птицей?
Что может путешествовать по свету, оставаясь в одном и том же углу?
Какими нотами можно измерить расстояние?

Логические задачи
1. Одному мастеру принесли семь цепей по 5 звеньев в каждой. Его попросили соединить их в одну непрерывную цепь. Он смог это сделать, при этом он разъединил и обратно соединил всего 5 звеньев. Как же ему это удалось?

Логические задачи
2. На одном острове находится мальчик и яблоня, на другом острове — бабушка. Между островами есть мост. Мальчику надо принести бабушке 2 яблока, но мост выдерживает только одного мальчика и одно яблоко. По мосту можно пройти только один раз. По воде плыть нельзя, по воздуху летать тоже нельзя, прорыть туннель тоже нельзя. Как ему перенести яблоки?