Слайд 2ПАРАДОКС СОРИТА (КУЧИ)
Одна песчинка – не куча.
Если одна песчинка – не куча,

то и две – не куча.
Если две – не куча, то и три не куча.
….
Если 99 999 песчинок – не куча, то и 100 000 – не куча.
Следовательно, 100 000 песчинок – не куча песка.
Но этот вывод очевидно не верен.
Что же пошло не так?
Слайд 3ВЫХОДЫ ИЗ ПАРАДОКСА СОРИТА
Настаивать, что существует момент, когда добавление одной песчинки

меняет ситуацию, что есть точное количество песчинок, после которого куча становится кучей.
Создание кучи не ограничивается серией добавлений по одной песчинки. Нет определённой точки перехода не кучи в кучу.
Слайд 4ПАРАДОКСЫ РАССЕЛА (ТЕОРИЯ ДЕСКРИПЦИЙ)
Информативное утверждение идентичности.
Если А и В идентичны, то

любое свойство А также является свойством В, и А может заменить В в любом предложении.
Пример: Катя хочет узнать, является ли А. С. Пушкин автором «Евгения Онегина». Поскольку Пушкин действительно автор «Евгения Онегина», замена приводит к тому, что Катя пытается узнать, действительно ли Пушкин – Пушкин
Слайд 5ПАРАДОКСЫ РАССЕЛА (ТЕОРИЯ ДЕСКРИПЦИЙ)
Сохранение законов логики.
По закону исключённого 3ьего, «если А

есть В» ложно, то «В не есть А» истинно.
То есть если утверждение «король Франции лыс» ложно, то «король Франции не лыс» должно быть истинно. Но это не так!
Слайд 6РЕШЕНИЕ ПАРАДОКСОВ: ПОДХОД РАССЕЛА
Определять правдивость утверждения должна логическая структура.
Рассел отбросил модель

«субъекта-предиката» (Ф есть Ж) и предложил такую модель:
Утверждение «Ф есть Ж» может быть разделено на 3 отдельных утверждения: «существует Ф», «существует только одно Ф», «если нечто является Ф, то оно является Ж».
Слайд 7РЕШЕНИЕ ПАРАДОКСОВ: ПОДХОД РАССЕЛА
Утверждение «Нынешний король Франции лыс» превращается в «есть

сущность, являющаяся королём Франции в данный момент, и такая сущность только одна, и эта сущность - лысая».
Утверждение ложно, но не потому, что король Франции не лыс, а потому, что «не существует сущности, являющейся королём Франции».






 Мораль
Мораль Современная русская философия
Современная русская философия Политическое учение Аристотеля
Политическое учение Аристотеля Философское понимание истины
Философское понимание истины 2_Filos_Drevnego_Vostoka
2_Filos_Drevnego_Vostoka Педагогические идеи первых общенаучных, философских систем
Педагогические идеи первых общенаучных, философских систем Как устроена общественная жизнь
Как устроена общественная жизнь Прагматизм. Представители прагматизма
Прагматизм. Представители прагматизма Античная философия: досократический период
Античная философия: досократический период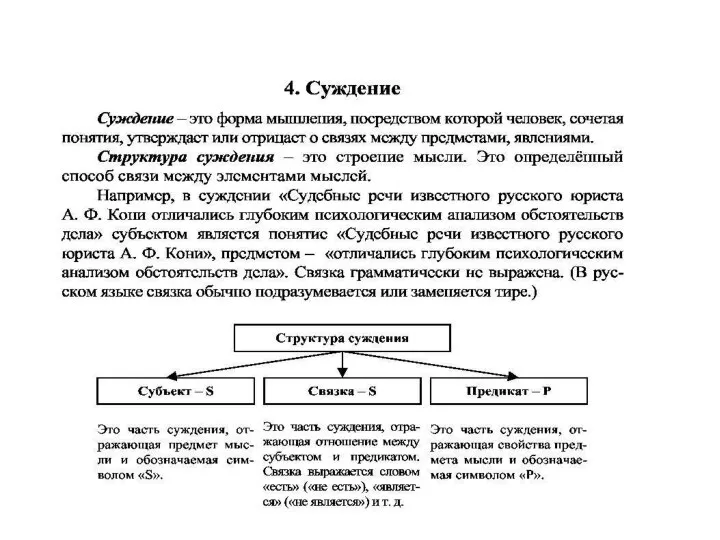 Суждение. Структура суждения
Суждение. Структура суждения Философия Древнего Китая
Философия Древнего Китая Научное познание
Научное познание Этапы чувственного познания. Ощущение, восприятие, представление
Этапы чувственного познания. Ощущение, восприятие, представление Материя, ее формы и атрибуты
Материя, ее формы и атрибуты Понятие как форма мышления
Понятие как форма мышления Жизнь и наследие Фрэнсиса Бэкона
Жизнь и наследие Фрэнсиса Бэкона Философская антропология. Ч.2
Философская антропология. Ч.2 فلسفة القرون الوسطى
فلسفة القرون الوسطى Динамика науки и метод
Динамика науки и метод Личность и человек
Личность и человек Философия Древней Индии Маминова Юлия
Философия Древней Индии Маминова Юлия Николя де Сталь
Николя де Сталь Наука и философия
Наука и философия Портреты философов
Портреты философов Античная философия
Античная философия Средневековая философия. Лекция 4. ч. 1
Средневековая философия. Лекция 4. ч. 1 Первые философы
Первые философы Категории человеческого бытия
Категории человеческого бытия