Содержание
- 2. Энергия — универсальная мера различных форм движения и взаимодействия материи. С различными формами движения материи связывают
- 3. Чтобы количественно характеризовать обмен энергией между взаимодействующими телами, в механике вводится понятие работы силы. Если тело
- 4. В общем случае сила может изменяться как по модулю, так и по направлению, поэтому формулой (11.1)
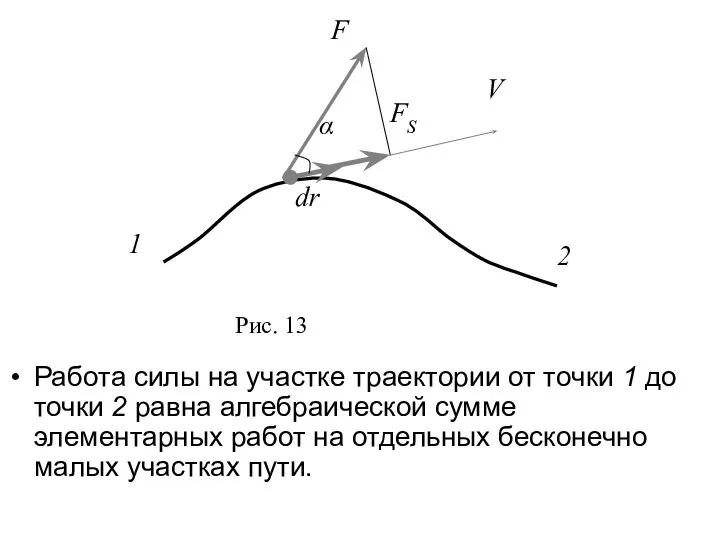
- 5. Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ
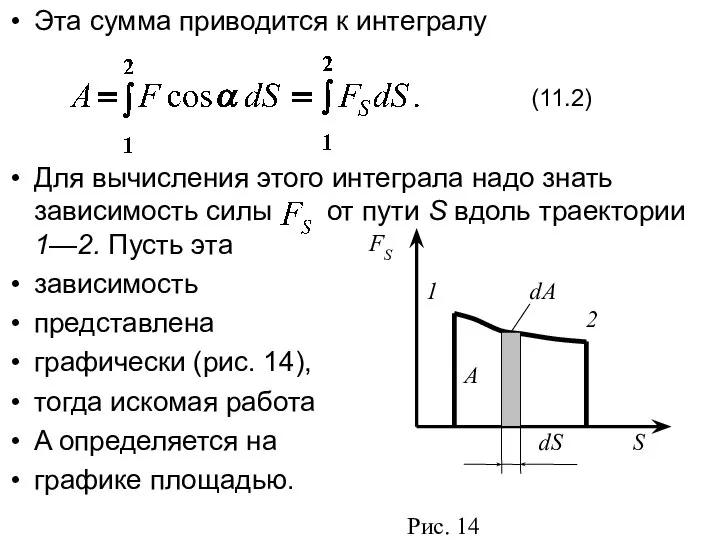
- 6. Эта сумма приводится к интегралу Для вычисления этого интеграла надо знать зависимость силы от пути S
- 7. Если, например, тело движется прямолинейно, сила F = const и α =const, то получим где S
- 8. Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности: За время dt сила совершает работу , и
- 9. § 12. Кинетическая и потенциальная энергии Кинетическая энергия механической системы — это энергия механического движения этой
- 10. Используя второй закон Ньютона и умножая обе части равенства на перемещение , получим Так как ,
- 11. Таким образом, тело массой т, движущееся со скоростью, обладает кинетической энергией Из формулы (12.1) видно, что
- 12. Потенциальная энергия — механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между
- 13. Тело, находясь в потенциальном поле сил, обладает потенциальной энергией П. Работа консервативных сил при элементарном (бесконечно
- 14. Для консервативных сил или в векторном виде Вектор, определяемый выражением (12.5), называется градиентом скаляра П. (12.4)
- 15. Наряду с обозначением grad П применяется также обозначение с помощью символического вектора, называемого оператором Гамильтона (У.
- 16. Так как начало отсчета выбирается произвольно, то потенциальная энергия может иметь отрицательное значение (кинетическая энергия всегда
- 17. — проекция силы упругости на ось х; k — коэффициент упругости (для пружины — жесткость), а
- 18. а полная работа идет на увеличение потенциальной энергии пружины. Таким образом, потенциальная энергия упругодеформированного тела Потенциальная
- 19. Полная механическая энергия системы — энергия механического движения и взаимодействия равна сумме кинетической и потенциальной энергий
- 20. § 13. Закон сохранения энергии Рассмотрим систему материальных точек массами , движущихся со скоростями . Пусть
- 21. При массы материальных точек постоянны и уравнения второго закона Ньютона для этих точек следующие: …………………………………… Двигаясь
- 22. Умножим каждое из выше представленных уравнений скалярно на соответствующее перемещение и, учитывая, что , получим: …………………………………………….
- 23. Первый член левой части равенства (13.1) где dT есть приращение кинетической энергии системы. Второй член (13.1)
- 24. Таким образом, имеем При переходе системы из состояния 1 в какое-либо состояние 2 т. е. изменение
- 25. Если внешние неконсервативные силы отсутствуют, то из (13.2) следует, что Откуда т. е. полная механическая энергия
- 26. Механические системы, на тела которых действуют только консервативные силы (внутренние и внешние), называются консервативными системами. Закон
- 27. Существует еще один вид систем — диссипативные системы, в которых механическая энергия постепенно уменьшается за счет
- 28. Закон сохранения и превращения энергии — фундаментальный закон природы, он справедлив как для систем макроскопических тел,
- 29. § 14. Графическое представление энергии Во многих задачах рассматривается одномерное движение тела, потенциальная энергия которого является
- 30. Потенциальная энергия тела массой т, поднятого на высоту h над поверхностью Земли, согласно (12.7), П(h) =
- 31. Из приведенного графика можно найти скорость тела на высоте h:
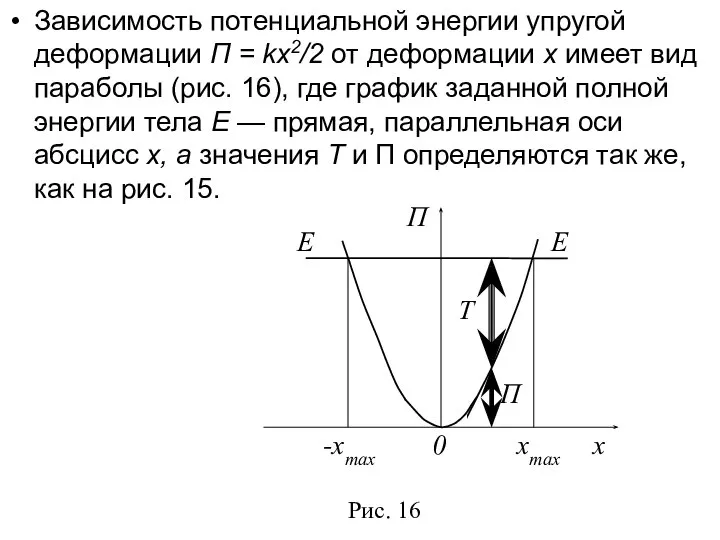
- 32. Зависимость потенциальной энергии упругой деформации П = kx2/2 от деформации х имеет вид параболы (рис. 16),
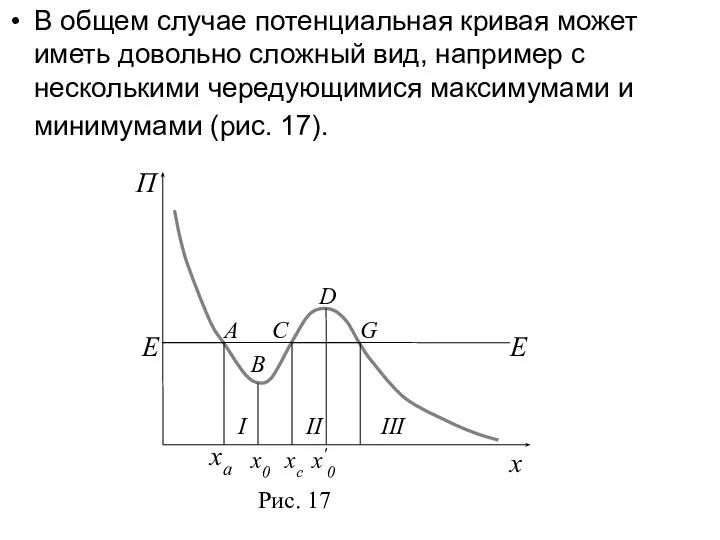
- 33. В общем случае потенциальная кривая может иметь довольно сложный вид, например с несколькими чередующимися максимумами и
- 34. § 15. Удар абсолютно упругих и неупругих тел Удар (или соударение) — это столкновение двух или
- 35. Тела во время удара претерпевают деформацию. Сущность удара заключается в том, что кинетическая энергия относительного движения
- 36. Если для сталкивающихся тел ε = 0, то такие тела называются абсолютно неупругими, если ε =
- 37. Прямая, проходящая через точку соприкосновения тел и нормальная к поверхности их соприкосновения, называется линией удара. Удар
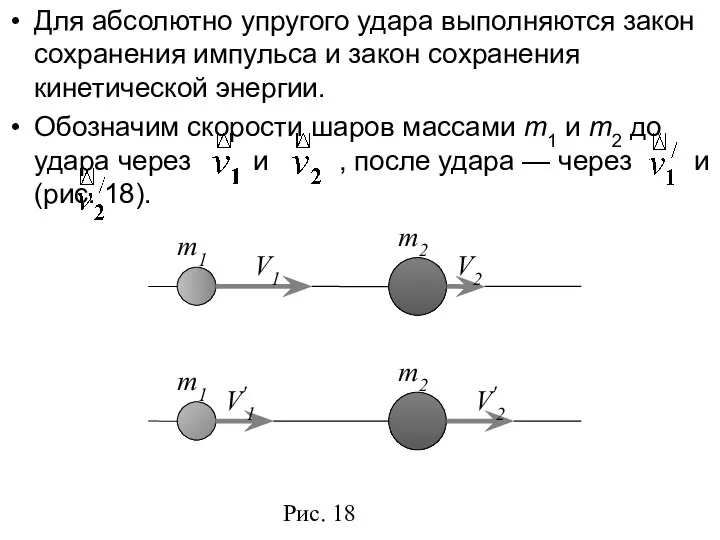
- 38. Для абсолютно упругого удара выполняются закон сохранения импульса и закон сохранения кинетической энергии. Обозначим скорости шаров
- 39. Для абсолютно упругого удара выполняются закон сохранения импульса и закон сохранения кинетической энергии. В этом случае
- 40. (15.3) разделив (15.4) на (15.3) получим: Решая уравнения (15.3) и (15.5), находим (15.4) (15.5)
- 41. (15.6) Рассмотрим несколько конкретных примеров. (15.7)
- 42. 1) При Проанализируем выражения (15.8) и (15.9) для двух шаров различных масс: (15.8) (15.9)
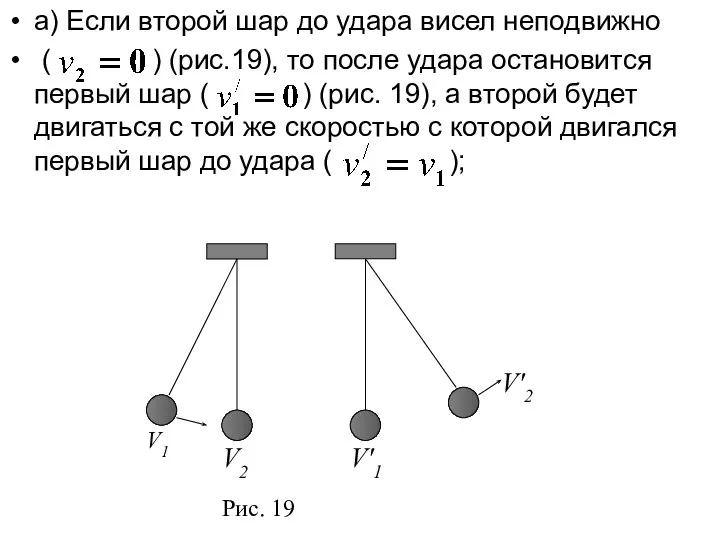
- 43. a) Если второй шар до удара висел неподвижно ( ) (рис.19), то после удара остановится первый
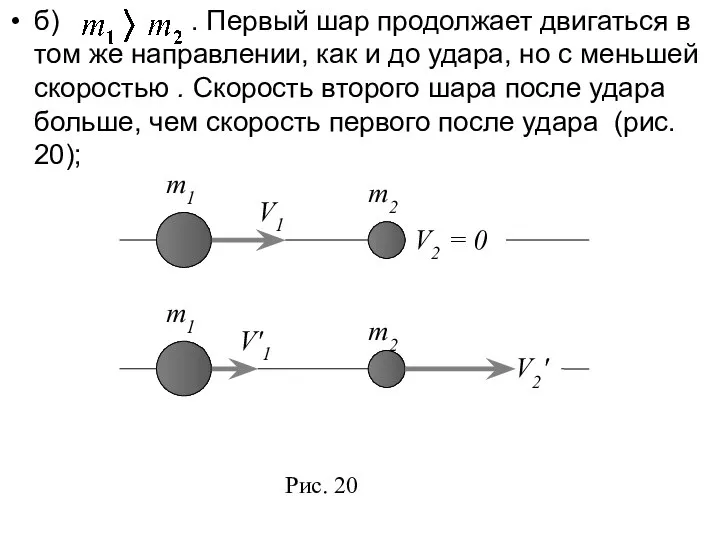
- 44. б) . Первый шар продолжает двигаться в том же направлении, как и до удара, но с
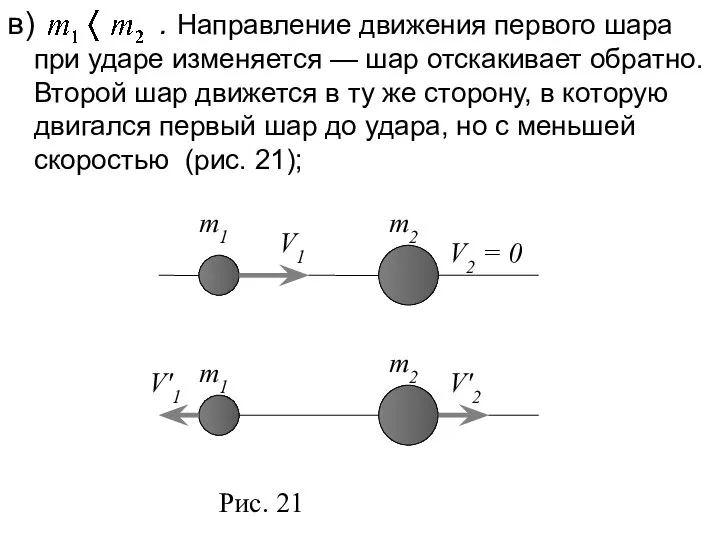
- 45. в) . Направление движения первого шара при ударе изменяется — шар отскакивает обратно. Второй шар движется
- 46. г) (например, столкновение шара со стеной). Из уравнений (15.8) и (15.9) следует, что 2) При выражения
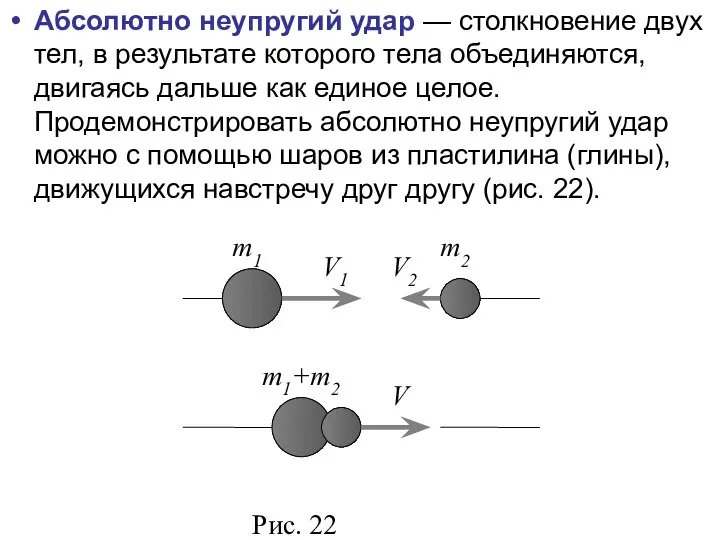
- 47. Абсолютно неупругий удар — столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое
- 48. Используя закон сохранения импульса, можно записать Откуда Если шары движутся навстречу друг другу, то они вместе
- 49. Выясним, как изменяется кинетическая энергия шаров при центральном абсолютно неупругом ударе. Так как в процессе соударения
- 50. Используя (15.10), получим Если ударяемое тело было первоначально неподвижно , то
- 52. Скачать презентацию








































 Вычисление массы и объёма тела по его плотности. 7 класс
Вычисление массы и объёма тела по его плотности. 7 класс Подготовка к практической работе. Задачи по физике
Подготовка к практической работе. Задачи по физике Презентация на тему Электромагнитные колебания
Презентация на тему Электромагнитные колебания  Давление газа
Давление газа Техническое обслуживание и ремонт электрических машин постоянного и переменного тока. Тест
Техническое обслуживание и ремонт электрических машин постоянного и переменного тока. Тест Физика вокруг нас. Конкурсная игра
Физика вокруг нас. Конкурсная игра Презентация на тему Сила трения покоя
Презентация на тему Сила трения покоя  Использование интернет – технологий в обучении физики
Использование интернет – технологий в обучении физики Ускорение свободного падения на Земле и других небесных телах
Ускорение свободного падения на Земле и других небесных телах Электрическая цепь
Электрическая цепь Комплексная механизация лесовосстановительных работ в Огудневском участковом лесничестве
Комплексная механизация лесовосстановительных работ в Огудневском участковом лесничестве Абсорбционная спектроскопия (поглощение света веществом)
Абсорбционная спектроскопия (поглощение света веществом) Коэффициент трения скольжения
Коэффициент трения скольжения Механическая работа. Мощность. Энергия. Закон сохранения и превращения энергии
Механическая работа. Мощность. Энергия. Закон сохранения и превращения энергии Последовательное и параллельное соединение
Последовательное и параллельное соединение Презентация на тему Атомная физика (11 класс)
Презентация на тему Атомная физика (11 класс)  Дисковая задвижка
Дисковая задвижка volnovye-yavleniya-
volnovye-yavleniya- Презентация на тему Манометры
Презентация на тему Манометры  11_ ОТС_ Модуляция и демодуляция 14
11_ ОТС_ Модуляция и демодуляция 14 Закон Ома и вычисление сопротивления. Решение задач
Закон Ома и вычисление сопротивления. Решение задач Теория горения и взрывов. Переход горения в детонацию. Взрыв. Лекция 10
Теория горения и взрывов. Переход горения в детонацию. Взрыв. Лекция 10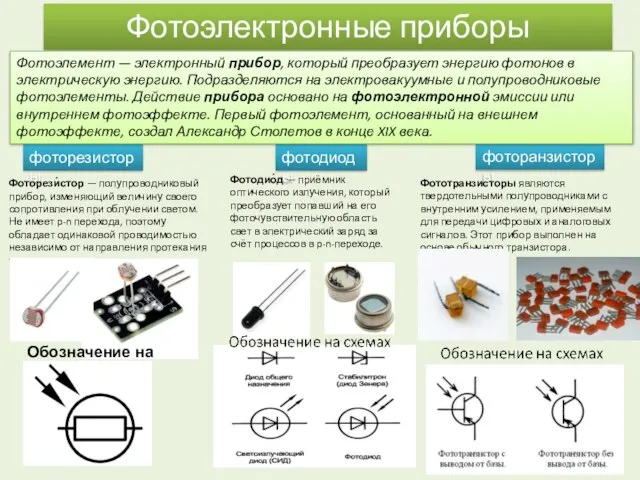 Фотоэлектронные приборы
Фотоэлектронные приборы Презентация на тему Скорость прямолинейного равноускоренного движения
Презентация на тему Скорость прямолинейного равноускоренного движения  Постоянный электрический ток
Постоянный электрический ток Найди ошибку
Найди ошибку Испарение. Насыщенный пар и его свойства. Влажность воздуха
Испарение. Насыщенный пар и его свойства. Влажность воздуха маятник. волны
маятник. волны