Содержание
- 2. На рис. показан проводник с током I, пронизывающий поверхность, ограниченную замкнутым контуром в виде окружности. Пусть
- 3. Путем опытов и расчетов установлено, что произведение напряженности поля H в точках контура на длину этого
- 4. В общем случае поверхность могут пронизывать несколько токов. Тогда определяют так называемый полный ток, т. е.
- 5. Например, применив закон полного тока для определения напряженности магнитного поля в то на стоянии r от
- 6. Переходя к магнитной индукции, будем иметь B = μaI/2πr, т. е. мы получили то же выражение
- 8. Скачать презентацию
Слайд 2На рис. показан проводник с током I, пронизывающий поверхность, ограниченную замкнутым контуром
На рис. показан проводник с током I, пронизывающий поверхность, ограниченную замкнутым контуром

в виде окружности. Пусть центр окружности лежит на оси проводника. В пространстве, окружающем проводник с током, возникает магнитное поле. Так как отдельные точки контура находятся от проводника на равных расстояниях, то напряженность поля, созданная током в каждой точке контура, будет также одинаковой. Направление вектора напряженности поля H зависит от направления тока в проводнике и определяется по "правилу буравчика". Вектор H располагается по касательной к окружности контура.
Слайд 3Путем опытов и расчетов установлено, что произведение напряженности поля H в точках
Путем опытов и расчетов установлено, что произведение напряженности поля H в точках

контура на длину этого контура l равно току I, пронизывающему поверхность, ограниченную данным контуром.
Таким образом,
H ⋅ l = I.
Таким образом,
H ⋅ l = I.
Слайд 4В общем случае поверхность могут пронизывать несколько токов. Тогда определяют так называемый
В общем случае поверхность могут пронизывать несколько токов. Тогда определяют так называемый

полный ток, т. е. находят алгебраическую сумму токов (∑I). Для этого случая можно записать:
H ⋅ l = ∑I.
Это выражение носит название закона полного тока. Закон полного тока является основным законом при расчете магнитных цепей и дает возможность в некоторых случаях легко определить напряженность поля.
H ⋅ l = ∑I.
Это выражение носит название закона полного тока. Закон полного тока является основным законом при расчете магнитных цепей и дает возможность в некоторых случаях легко определить напряженность поля.
Слайд 5Например, применив закон полного тока для определения напряженности магнитного поля в то
Например, применив закон полного тока для определения напряженности магнитного поля в то

на стоянии r от бесконечно длинного прямолинейного проводника с током (рис.), имеем следующее: полный ток равен току в проводнике ∑I = I; контур, проведенный на расстоянии r от проводника, совпадает с магнитной линией; длина контура l будет l = 2πr, поэтому H ⋅ 2πl = I, откуда H = I/2πr.
Слайд 6Переходя к магнитной индукции, будем иметь B = μaI/2πr, т. е. мы
Переходя к магнитной индукции, будем иметь B = μaI/2πr, т. е. мы

получили то же выражение для магнитной индукции, которое было приведено выше Для такого же случая. Применим закон полного тока для определения напряженности поля по оси катушки, равномерно намотанной на кольцо (рис.). Контуром здесь является ось катушки (она же ось кольца). Площадь контура пронизывает полный ток, равный произведению тока I на число витков ω катушки, т. е. ∑I = Iω. Обозначив длину оси катушки через l, запишем закон полного тока:
H ⋅ l = Iω,
откуда
H = Iω/l,
или, переходя к магнитной индукции, будем иметь
В = μа I⋅ω/l.
H ⋅ l = Iω,
откуда
H = Iω/l,
или, переходя к магнитной индукции, будем иметь
В = μа I⋅ω/l.
- Предыдущая
Управление ФНБ Анализ питьевых вод
Анализ питьевых вод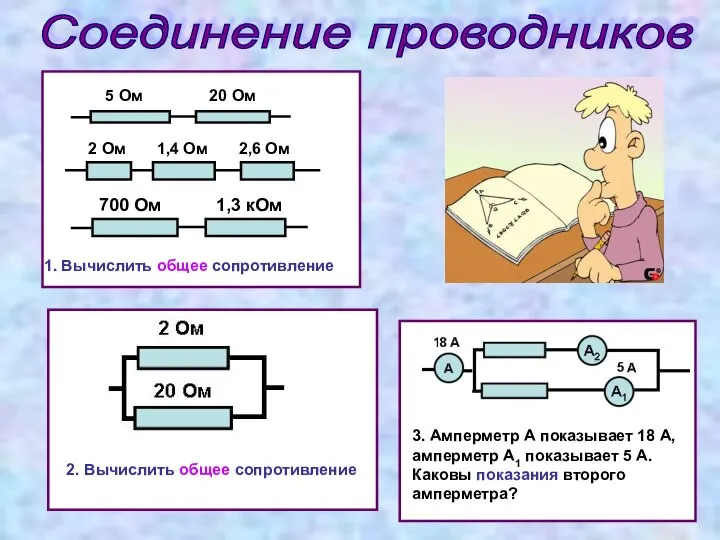 Соединение проводников
Соединение проводников Презентация по физике "Электростатика. Электрические заряды" -
Презентация по физике "Электростатика. Электрические заряды" -  Итоговый тест на тему: Изменение агрегатных состояний вещества
Итоговый тест на тему: Изменение агрегатных состояний вещества Кинематика. 9 класс. Контрольная работа
Кинематика. 9 класс. Контрольная работа Физическая викторина
Физическая викторина Источники электрического тока
Источники электрического тока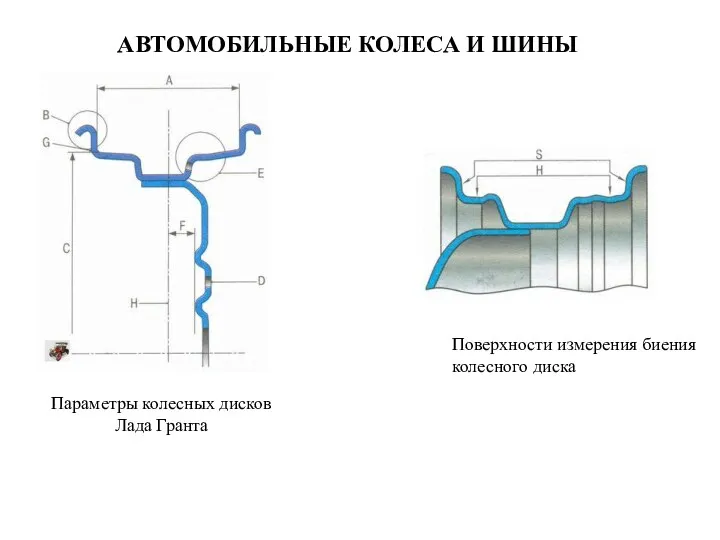 Автомобильные колеса и шины. Поверхности измерения биения колесного диска. Параметры колесных дисков Лада Гранта
Автомобильные колеса и шины. Поверхности измерения биения колесного диска. Параметры колесных дисков Лада Гранта Триггеры и сумматоры Устройства АЛУ
Триггеры и сумматоры Устройства АЛУ Работа и мощность. Решение задач
Работа и мощность. Решение задач Технология формирования пленок оксида свинца
Технология формирования пленок оксида свинца Изменение агрегатных состояний вещества. Решение задач
Изменение агрегатных состояний вещества. Решение задач Силы в природе. 10 класс
Силы в природе. 10 класс Система термической стабилизации масла в системе смазки подшипников скольжения
Система термической стабилизации масла в системе смазки подшипников скольжения Сила упругости. Закон Гука
Сила упругости. Закон Гука Электричество и магнетизм. Лекция № 1
Электричество и магнетизм. Лекция № 1 Молекулярная физика. Тепловые явления
Молекулярная физика. Тепловые явления Введение в специальность Квантовая метрология. Ядерные часы
Введение в специальность Квантовая метрология. Ядерные часы Физико-математическая викторина для учащихся 7-8 классов
Физико-математическая викторина для учащихся 7-8 классов Приводные муфты
Приводные муфты Закон электромагнитной индукции. Правило Ленца. Явление самоиндукции. Индуктивность
Закон электромагнитной индукции. Правило Ленца. Явление самоиндукции. Индуктивность Лист лотоса. Оптические и СЗМ изображения
Лист лотоса. Оптические и СЗМ изображения Презентация на тему Тепловые двигатели 10 класс
Презентация на тему Тепловые двигатели 10 класс  Измерение фокусного расстояния собирающей линзы. Получение изображений при помощи линзы
Измерение фокусного расстояния собирающей линзы. Получение изображений при помощи линзы Механические колебания. Колебательные движения
Механические колебания. Колебательные движения Автомобили III
Автомобили III Конденсаторы. Электроёмкость конденсатора. Энергия заряжённого конденсатора. Применение конденсаторов
Конденсаторы. Электроёмкость конденсатора. Энергия заряжённого конденсатора. Применение конденсаторов Тема 1.2 Нормир.точности. продолжение
Тема 1.2 Нормир.точности. продолжение