4. Механика твердого тела

В случае непрерывного распределения масс эта сумма сводится к интегралу
где интегрирование производится по всему объему тела.
Величина r в этом случае есть функция положения точки с координатами х, у, z.

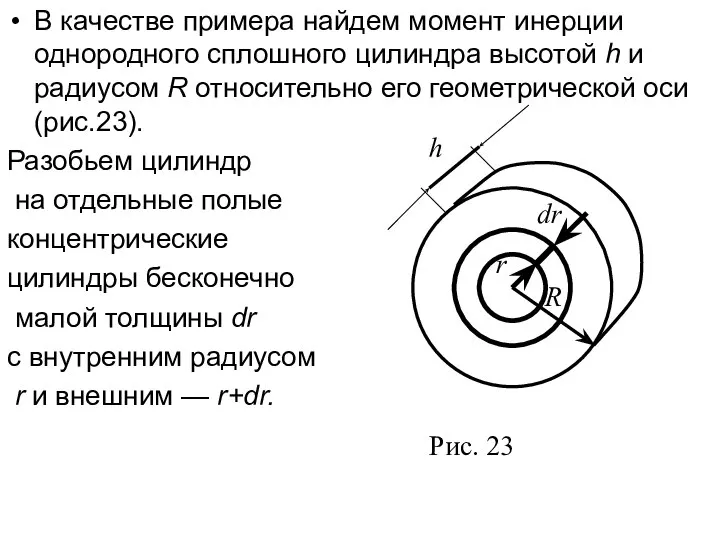
В качестве примера найдем момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси (рис.23).
Разобьем цилиндр
на отдельные полые
концентрические
цилиндры бесконечно
малой толщины dr
с внутренним радиусом
r и внешним — r+dr.

Момент инерции каждого полого цилиндра dJ = r2dm (так как dr << r, то считаем, что расстояние всех точек цилиндра от оси равно r), где dm — масса всего элементарного цилиндра; а его объем 2πrh dr.
Если ρ — плотность материала, то dm = ρ 2πrh dr и dJ = 2πhρrзdr. Тогда момент инерции сплошного цилиндра
но так как πR2h — объем цилиндра, то его масса m = πR2hρ, а момент инерции

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера:
момент инерции тела J относительно любой оси вращения равен моменту его инерции относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы т тела на квадрат расстояния а между осями:
(16.1)

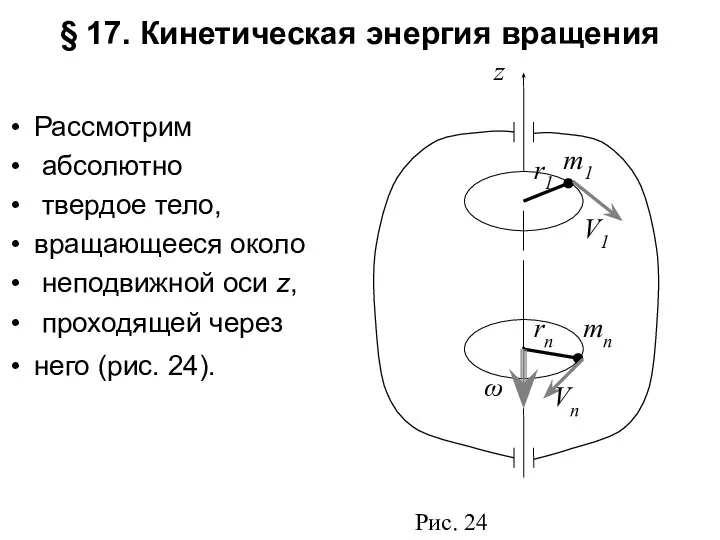
§ 17. Кинетическая энергия вращения
Рассмотрим
абсолютно
твердое тело,
вращающееся около
неподвижной оси z,
проходящей через
него (рис. 24).

Мысленно разобьем это тело на маленькие объемы с элементарными массами , находящиеся на расстоянии от оси вращения.
При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами описывают окружности различных радиусов и имеют различные линейные скорости.
Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:
(17.1)

Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:
Или
Используя выражение (17.1), получим

Таким образом, кинетическая энергия вращающегося тела
Из сравнения формулы (17.2) с выражением (12.1) для кинетической энергии тела, движущегося поступательно , следует, что момент инерции вращательного движения — мера инертности тела.
Формула (17.2) справедлива для тела, вращающегося вокруг неподвижной оси.
(17.2)

В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:
—момент инерции тела относительно оси, проходящей через его центр масс

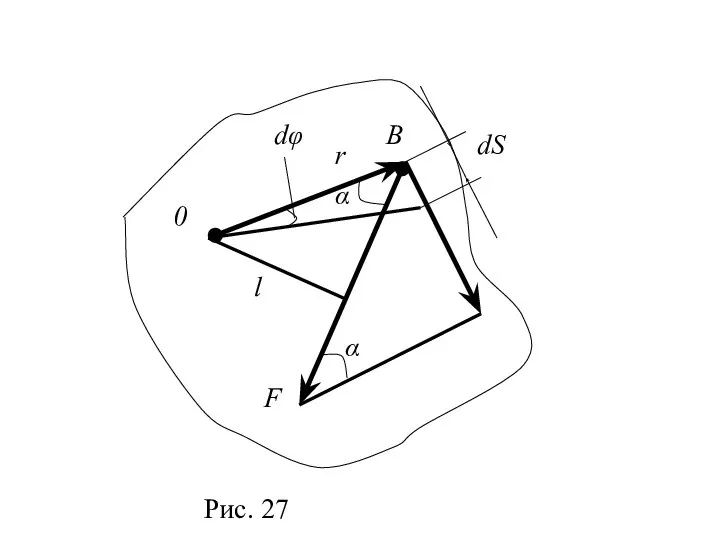
§ 18. Момент силы. Уравнение динамики вращательного движения твердого тела
Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора, проведенного из точки О в точку А приложения силы, на силу (рис. 25):
Модуль момента силы
(18.1)

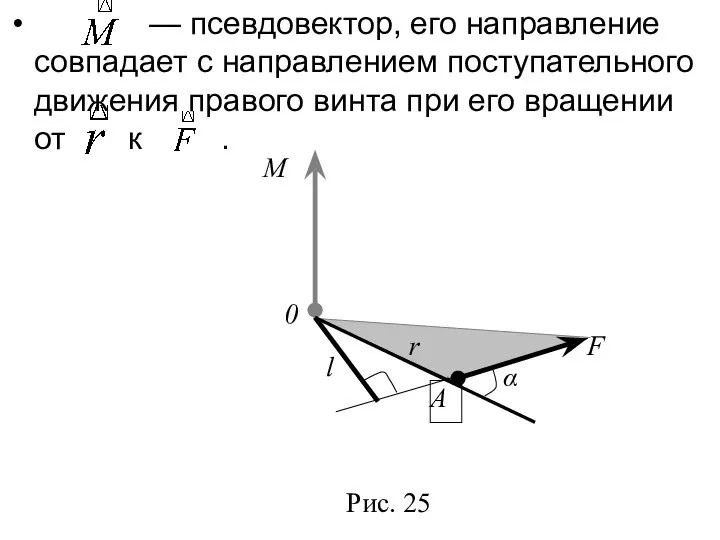
— псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к .

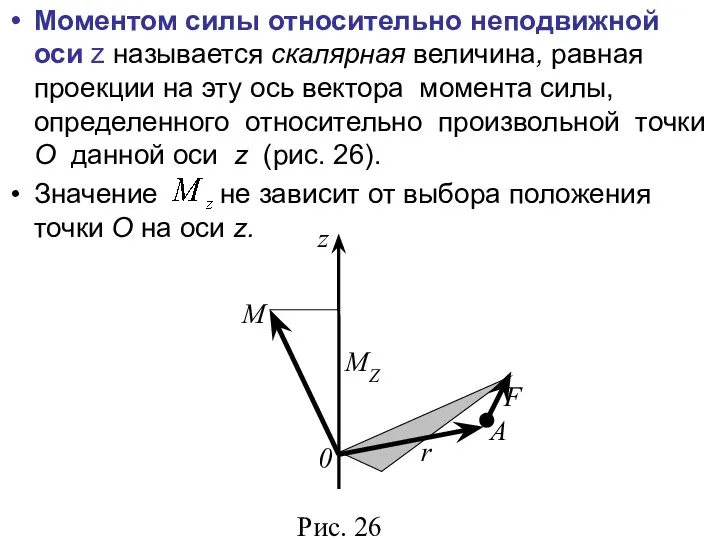
Моментом силы относительно неподвижной оси z называется скалярная величина, равная проекции на эту ось вектора момента силы, определенного относительно произвольной точки О данной оси z (рис. 26).
Значение не зависит от выбора положения точки О на оси z.

Если ось z совпадает с направлением вектора , то момент силы представляется в виде вектора, совпадающего с осью:
Найдем выражение для работы при вращении тела (рис. 27).
Пусть сила приложена в точке В, находящейся от оси вращения на расстоянии , α — угол между направлением силы и радиусом-вектором
Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела.

При повороте тела на бесконечно малый угол точка приложения В проходит путь , и работа равна произведению проекции силы на направление смещения на величину смещения:
Учитывая (18.1), можем записать
где
Таким образом, работа при вращении тела равна произведению момента действующей силы на угол поворота.
(18.2)

Работа при вращении тела идет на увеличение его кинетической энергии:
но
поэтому
или

Учитывая, что , получим
Уравнение (18.3) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.
Можно показать, что если ось вращения совпадает с главной осью инерции (см. § 20), проходящей через центр масс, то имеет место векторное равенство
(18.3)
(18.4)

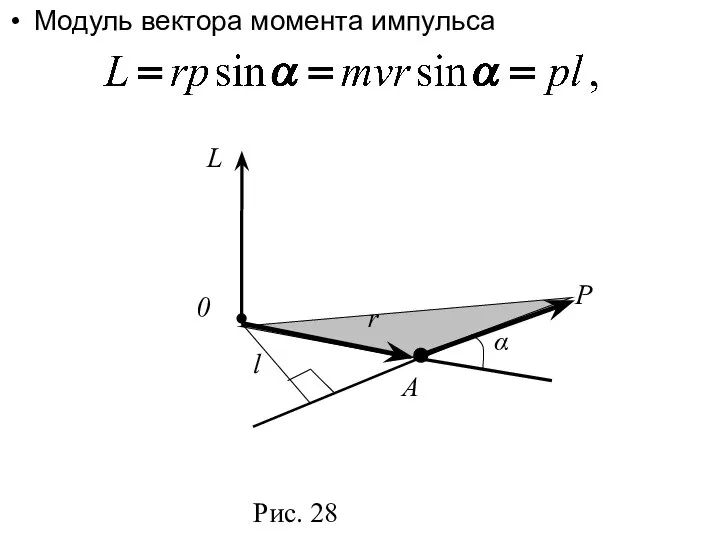
§ 19. Момент импульса и
закон его сохранения
Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
где — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к .

Модуль вектора момента импульса

Моментом импульса относительно неподвижной оси z называется скалярная величина , равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Значение момента импульса не зависит от положения точки О на оси z.
При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдельная точка тела движется по окружности постоянного радиуса , с некоторой скоростью .
Скорость и импульс перпендикулярны этому радиусу, т.е. радиус является плечом вектора .

Поэтому можем записать, что момент импульса отдельной частицы
и направлен по оси в сторону, определяемую правилом правого винта.
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных его частиц:
Учитывая, что
(19.1)

Получим
т.е.
Продифференцируем уравнение (19.2) по времени:
т.е.
(19.2)

Можно показать, что имеет место векторное равенство
В замкнутой системе и
поэтому
Выражение (19.4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.
(19.3)
(19.4)

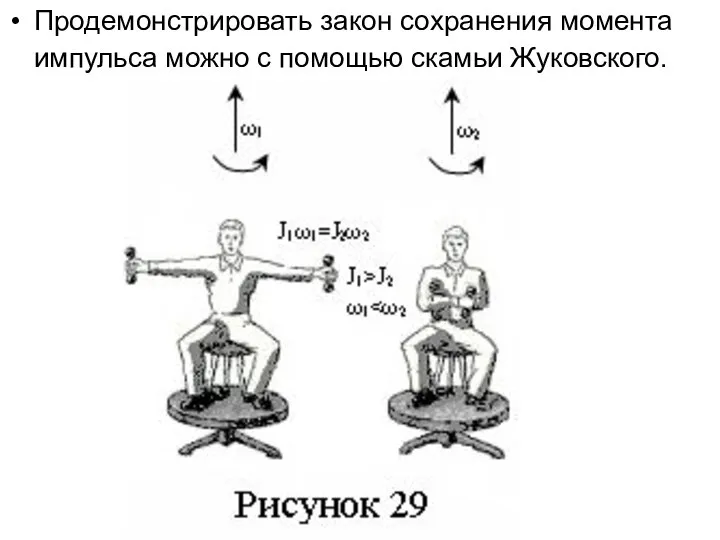
Продемонстрировать закон сохранения момента импульса можно с помощью скамьи Жуковского.

§ 20. Свободные оси. Гироскоп
Для того чтобы сохранить положение оси вращения твердого тела с течением времени неизменным, используют подшипники, в которых она удерживается.
Однако существуют такие оси вращения тел, которые не изменяют своей ориентации в пространстве без действия на нее внешних сил. Эти оси называются свободными осями (или осями свободного вращения).
Можно доказать, что в любом теле существуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями (они называются главными осями инерции тела).

Главные оси инерции однородного прямоугольного параллелепипеда проходят через центры противоположных граней (рис. 30).
Для однородного цилиндра одной из главных осей инерции является его геометрическая ось, а в качестве остальных осей могут быть две любые взаимно перпендикулярные оси, проведенные через центр масс в плоскости, перпендикулярной геометрической оси цилиндра.
Главными осями инерции шара являются любые три взаимно перпендикулярные оси, проходящие через центр масс.
Вращение вокруг главных осей с наибольшим и наименьшим моментами инерции устойчиво, а вращение около оси со средним моментом — неустойчиво.

Свойство свободных осей сохранять свое положение в пространстве широко применяется в технике.
Наиболее интересны в этом плане гироскопы — массивные однородные тела, вращающиеся с большой угловой скоростью вдоль своей оси симметрии, являющейся свободной осью.
Пока гироскоп неподвижен, его оси можно придать любое направление.
Если начать гироскоп быстро вращать и поворачивать его подставку, то ось гироскопа сохраняет свое положение в пространстве неизменной.
Это объясняется тем, что момент силы тяжести относительно закрепленного центра масс равен нулю.

Гироскоп

§ 21. Деформации твердого тела
Рассматривая механику твердого тела, мы пользовались понятием абсолютно твердого тела. Однако в природе абсолютно твердых тел нет, так как все реальные тела под действием сил изменяют свою форму и размеры, т. е. деформируются.
Деформация называется упругой, если после прекращения действия внешних сил тело принимает первоначальные размеры и форму. Деформации, которые сохраняются в теле после прекращения действия внешних сил, называются пластическими (или остаточными).

Реальные тела под действием внешних сил, как правило, испытывают упругие и пластические деформации, так как они после прекращения действия внешних сил никогда полностью не исчезают. Однако если остаточные деформации малы, то ими можно пренебречь и рассматривать лишь упругие деформации, что мы и будем делать.
В теории упругости доказывается, что все виды деформаций (растяжение или сжатие, сдвиг, изгиб, кручение) могут быть сведены к одновременно происходящим деформациям растяжения или сжатия и сдвига.

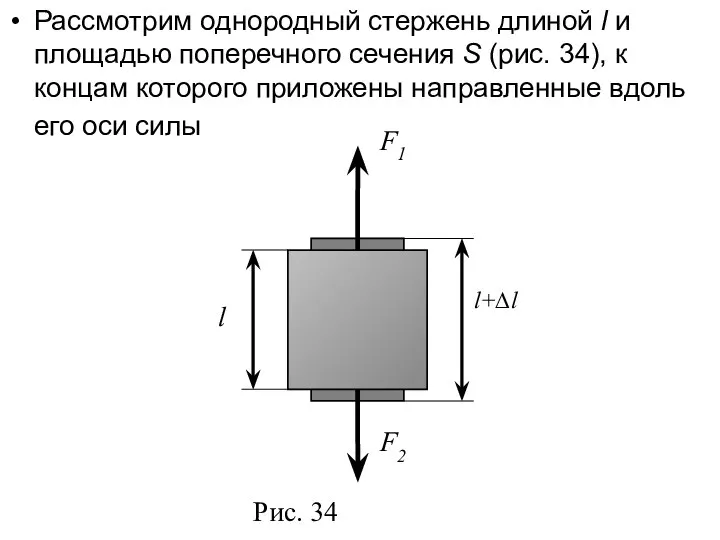
Рассмотрим однородный стержень длиной l и площадью поперечного сечения S (рис. 34), к концам которого приложены направленные вдоль его оси силы

Сила, действующая на единицу площади поперечного сечения, называется напряжением:
Если сила направлена по нормали к поверхности, напряжение называется нормальным, если же по касательной к поверхности — тангенциальным.
Количественной мерой, характеризующей степень деформации, испытываемой телом, является его относительная деформация.
(21.1)

Так, относительное изменение длины стержня (продольная деформация)
относительное поперечное растяжение (сжатие)
где d — диаметр стержня.
Деформации и всегда имеют разные знаки. Из опыта вытекает их взаимосвязь:
где — положительный коэффициент (коэффициентом Пуассона) , зависящий от свойств материала.
(21.2)

Английский физик Р. Гук экспериментально установил, что для малых деформаций относительное удлинение и напряжение прямо пропорциональны друг другу:
где коэффициент пропорциональности Е называется модулем Юнга.
Из выражения (21.3) видно, что модуль Юнга определяется напряжением, вызывающим относительное удлинение, равное единице. Из формул (21.2), (21.3) и (21.1) вытекает, что
(21.3)

Или
где k — коэффициент упругости.
Выражение (21.4) также задает закон Гука, согласно которому удлинение стержня при упругой деформации пропорционально действующей на стержень силе.
Деформации твердых тел подчиняются закону Гука лишь в очень узких пределах (до предела пропорциональности ).
При дальнейшем увеличении напряжения зависимость уже нелинейна, хотя деформация еще упругая вплоть до предела упругости ( ) и остаточные деформации не возникают.
(21.4)

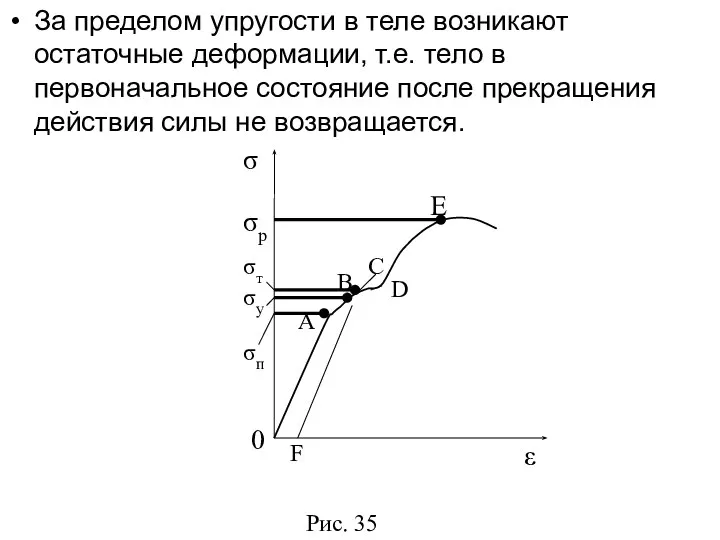
За пределом упругости в теле возникают остаточные деформации, т.е. тело в первоначальное состояние после прекращения действия силы не возвращается.

Напряжение, при котором появляется заметная остаточная деформация (≈ 0,2 %), называется пределом текучести ( ).
При этом деформация возрастает без увеличения напряжения, т. е. тело как бы «течет». Эта область называется областью текучести (или областью пластических деформаций).
Материалы, для которых область текучести значительна, называются вязкими, а для которых область текучести практически отсутствует — хрупкими.
При дальнейшем растяжении тела происходит его разрушение. Максимальное напряжение, возникающее в теле до разрушения, называется пределом прочности ( )

Одно и то же твердое тело может при кратковременном действии сил проявлять себя как хрупкое, а при длительных, но слабых силах является текучим.
Вычислим потенциальную энергию упруго растянутого (сжатого) стержня, которая равна работе, совершаемой внешними силами при деформации:
где х — абсолютное удлинение стержня, изменяющееся в процессе деформации от 0 до
Согласно закону Гука (21.4), .

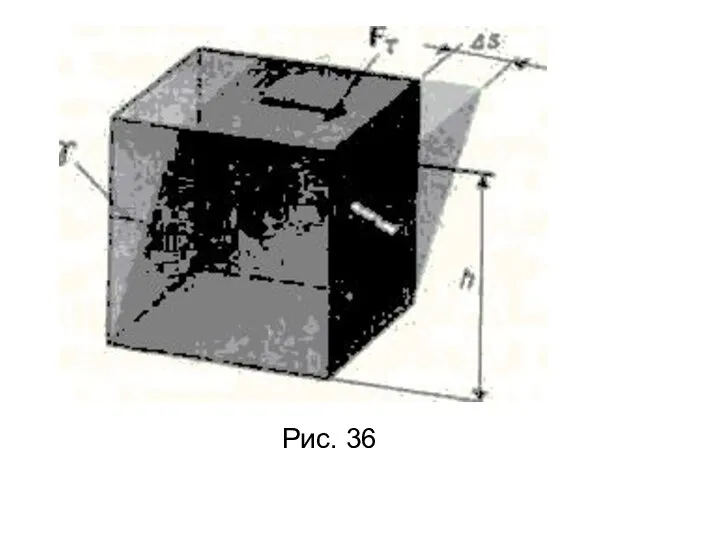
Поэтому
т. е. потенциальная энергия упругорастянутого стержня пропорциональна квадрату деформации.
Деформацию сдвига проще всего осуществить, если взять брусок, имеющий форму прямоугольного параллелепипеда, и приложить к нему силу (рис.36), касательную к его поверхности (нижняя часть бруска закреплена неподвижно).

Рис. 36