Численное решение теплепроводностью

ЦЕЛЬ РАБОТЫ
В работе рассматривается процесс прогрева и распространения тепла между составными частями конструкции, обладающими различными теплофизическими характеристиками.
Цель данной работы состоит в нахождении численного решения одномерного уравнения теплопроводности с граничными условиями первого, третьего и четвертого рода с использованием неявной разностной схемы.

ВВЕДЕНИЕ
При рассмотрении многих явлений в природе и технике важную роль играет теплопроводность.
Так, например, при строительстве современных домов используются многослойные конструкции с различными теплофизическими свойствами, огнестойкость которых должна удовлетворять требованиям пожарной безопасности.
Разработке различных расчетных методов для оценки огнестойкости разрабатываемых конструкций уделяется особое внимание.
Огнезащита такого рода конструкций может быть выполнена отделкой негорючими теплоизоляционными материалами, окрашиванием специальными красками или оштукатуриваем.

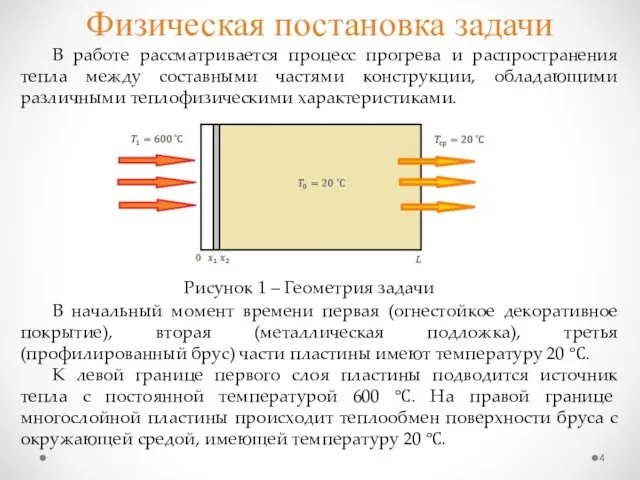
Физическая постановка задачи
В работе рассматривается процесс прогрева и распространения тепла между составными частями конструкции, обладающими различными теплофизическими характеристиками.
В начальный момент времени первая (огнестойкое декоративное покрытие), вторая (металлическая подложка), третья (профилированный брус) части пластины имеют температуру 20 °С.
К левой границе первого слоя пластины подводится источник тепла с постоянной температурой 600 °С. На правой границе многослойной пластины происходит теплообмен поверхности бруса с окружающей средой, имеющей температуру 20 °С.
Рисунок 1 – Геометрия задачи

Математическая постановка задачи

Математическая постановка задачи

Дискретизация

Построение конечно-разностного аналога
Полученную систему линейных алгебраических уравнений (3.2) будем решать методом прогонки.

Порядок аппроксимации неявной схемы
коэффициент температуропроводности.

Устойчивость

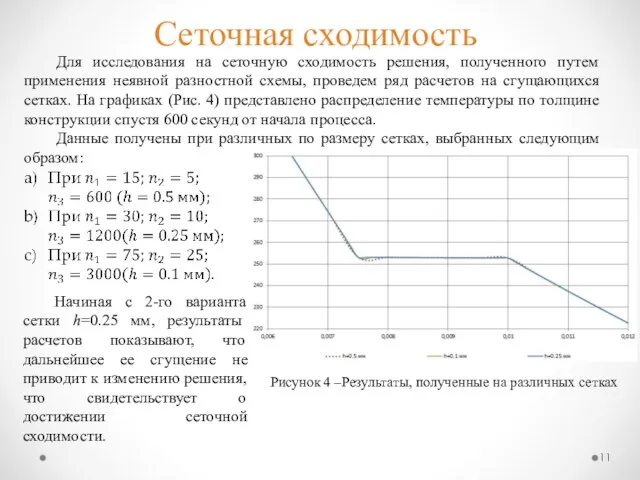
Сеточная сходимость
Для исследования на сеточную сходимость решения, полученного путем применения неявной разностной схемы, проведем ряд расчетов на сгущающихся сетках. На графиках (Рис. 4) представлено распределение температуры по толщине конструкции спустя 600 секунд от начала процесса.
Данные получены при различных по размеру сетках, выбранных следующим образом:
Начиная с 2-го варианта сетки h=0.25 мм, результаты расчетов показывают, что дальнейшее ее сгущение не приводит к изменению решения, что свидетельствует о достижении сеточной сходимости.
Рисунок 4 –Результаты, полученные на различных сетках

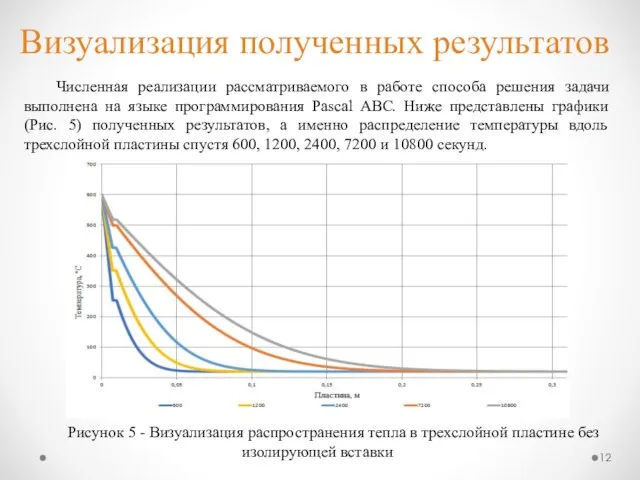
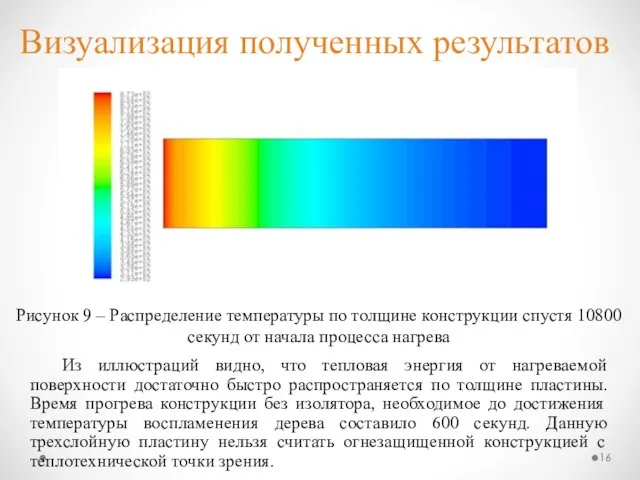
Визуализация полученных результатов
Численная реализации рассматриваемого в работе способа решения задачи выполнена на языке программирования Pascal ABC. Ниже представлены графики (Рис. 5) полученных результатов, а именно распределение температуры вдоль трехслойной пластины спустя 600, 1200, 2400, 7200 и 10800 секунд.
Рисунок 5 - Визуализация распространения тепла в трехслойной пластине без изолирующей вставки

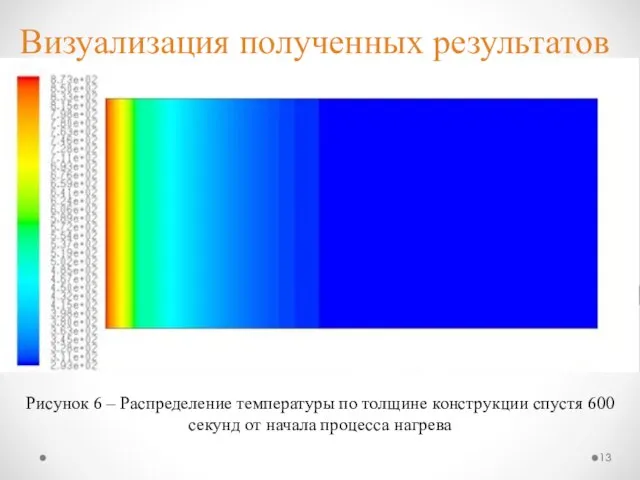
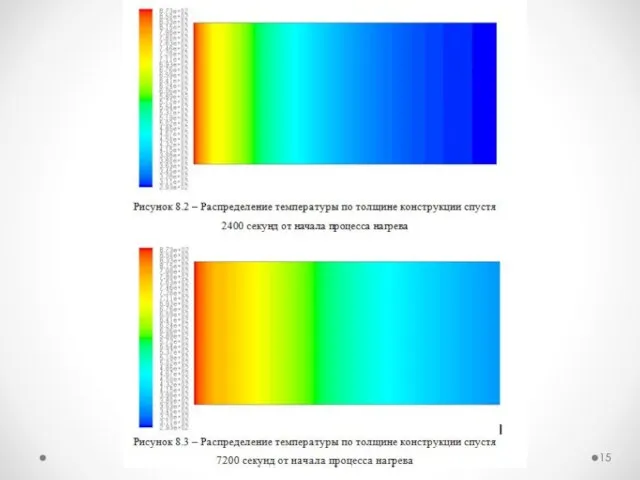
Визуализация полученных результатов
Рисунок 6 – Распределение температуры по толщине конструкции спустя 600 секунд от начала процесса нагрева

Визуализация полученных результатов
Рисунок 7 – Распределение температуры по толщине конструкции спустя 1200 секунд от начала процесса нагрева

Из иллюстраций видно, что тепловая энергия от нагреваемой поверхности достаточно быстро распространяется по толщине пластины. Время прогрева конструкции без изолятора, необходимое до достижения температуры воспламенения дерева составило 600 секунд. Данную трехслойную пластину нельзя считать огнезащищенной конструкцией с теплотехнической точки зрения.
Визуализация полученных результатов
Рисунок 9 – Распределение температуры по толщине конструкции спустя 10800 секунд от начала процесса нагрева

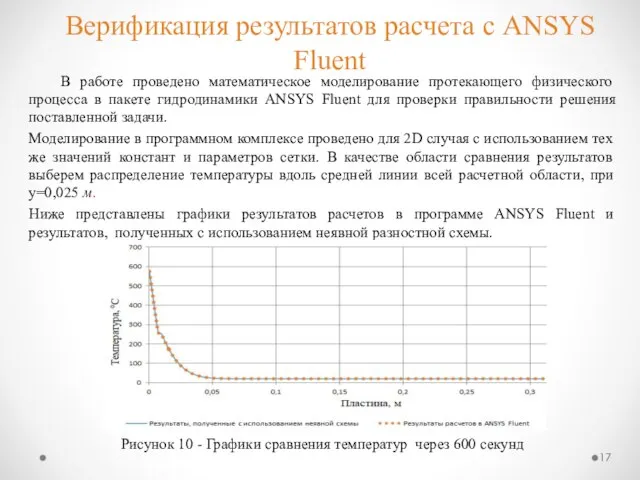
Верификация результатов расчета с ANSYS Fluent
В работе проведено математическое моделирование протекающего физического процесса в пакете гидродинамики ANSYS Fluent для проверки правильности решения поставленной задачи.
Моделирование в программном комплексе проведено для 2D случая с использованием тех же значений констант и параметров сетки. В качестве области сравнения результатов выберем распределение температуры вдоль средней линии всей расчетной области, при y=0,025 м.
Ниже представлены графики результатов расчетов в программе ANSYS Fluent и результатов, полученных с использованием неявной разностной схемы.
Рисунок 10 - Графики сравнения температур через 600 секунд

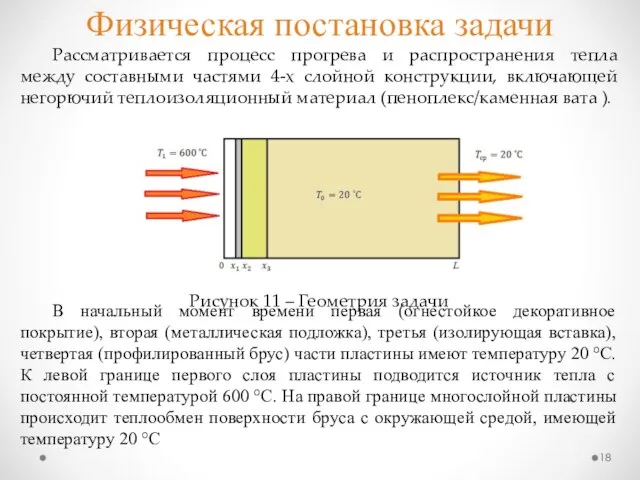
Физическая постановка задачи
Рассматривается процесс прогрева и распространения тепла между составными частями 4-х слойной конструкции, включающей негорючий теплоизоляционный материал (пеноплекс/каменная вата ).
В начальный момент времени первая (огнестойкое декоративное покрытие), вторая (металлическая подложка), третья (изолирующая вставка), четвертая (профилированный брус) части пластины имеют температуру 20 °С. К левой границе первого слоя пластины подводится источник тепла с постоянной температурой 600 °С. На правой границе многослойной пластины происходит теплообмен поверхности бруса с окружающей средой, имеющей температуру 20 °С
Рисунок 11 – Геометрия задачи

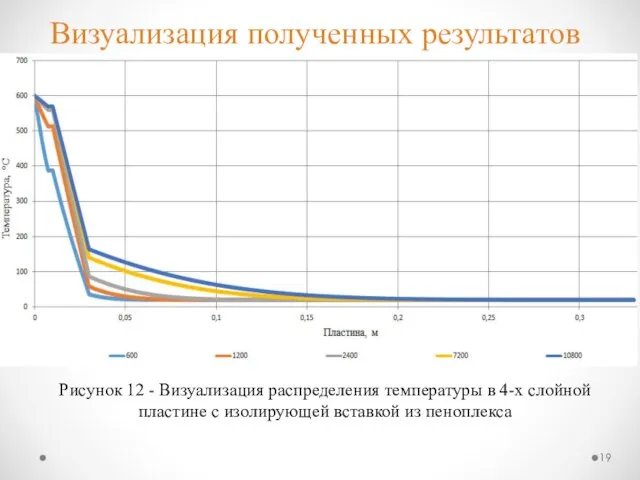
Визуализация полученных результатов
Рисунок 12 - Визуализация распределения температуры в 4-х слойной пластине с изолирующей вставкой из пеноплекса

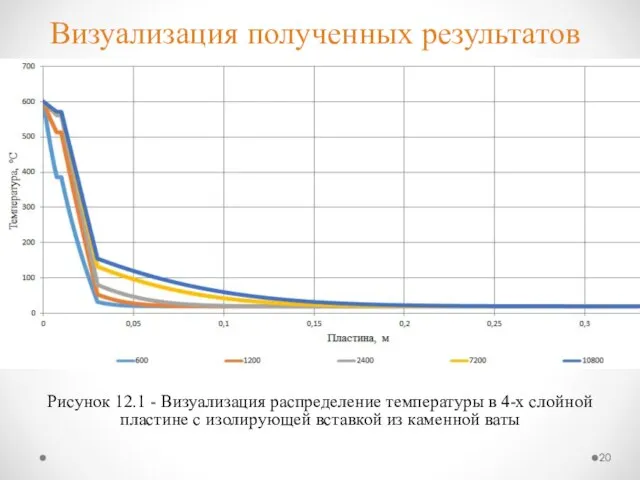
Рисунок 12.1 - Визуализация распределение температуры в 4-х слойной пластине с изолирующей вставкой из каменной ваты
Визуализация полученных результатов

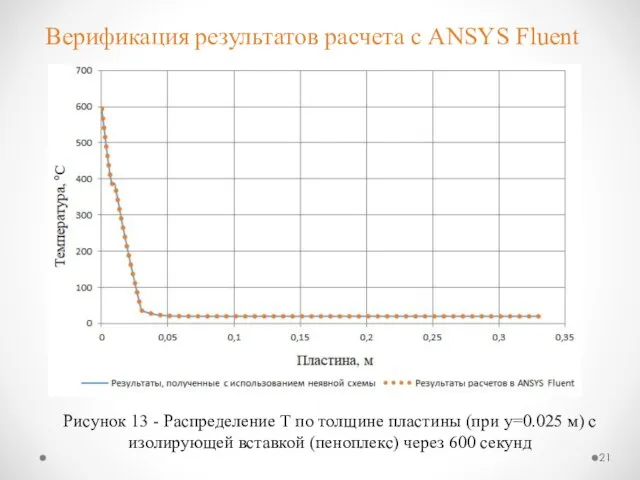
Верификация результатов расчета с ANSYS Fluent
Рисунок 13 - Распределение Т по толщине пластины (при y=0.025 м) с изолирующей вставкой (пеноплекс) через 600 секунд

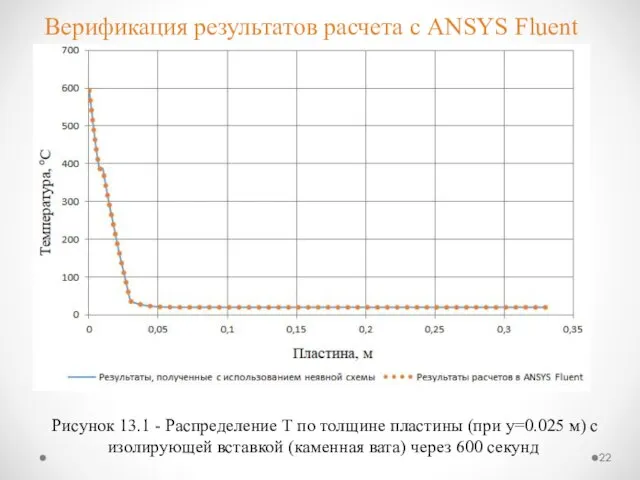
Рисунок 13.1 - Распределение Т по толщине пластины (при y=0.025 м) с изолирующей вставкой (каменная вата) через 600 секунд
Верификация результатов расчета с ANSYS Fluent

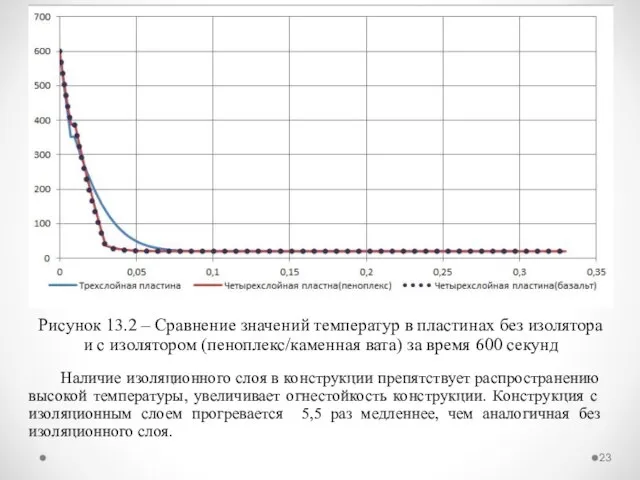
Рисунок 13.2 – Сравнение значений температур в пластинах без изолятора и с изолятором (пеноплекс/каменная вата) за время 600 секунд
Наличие изоляционного слоя в конструкции препятствует распространению высокой температуры, увеличивает огнестойкость конструкции. Конструкция с изоляционным слоем прогревается 5,5 раз медленнее, чем аналогичная без изоляционного слоя.

Рисунок 14 - Распределение температуры по
толщине конструкции без изолятора
спустя 600 секунд от начала процесса
Визуализация полученных результатов
Рисунок 14.1 - Распределение температуры по
толщине конструкции с изоляционным
слоем из пеноплекса спустя 600 секунд
от начала процесса

ЗАКЛЮЧЕНИЕ
Из результатов моделирования следует, что четырехслойная конструкция, содержащая изолятор из пеноплекса или каменной ваты прогревается значительно медленнее, чем аналогичная конструкция без изолирующей вставки.
Рассматриваемую в работе четырехслойную пластину с теплотехнической точки зрения можно уже считать огнезащищенной конструкцией.
Это подтверждает использование данных негорючих теплоизоляционных материалов для выполнения огнезащиты подобных многослойных конструкций и увеличение их огнестойкости.

СПИСОК ЛИТЕРАТУРЫ
Сиковский Д.Ф. Методы вычислительной теплофизики / Д.Ф. Сиковский. – Изд-во Новосиб. гос. ун-та, 2013. –98 с.
Исаков Г.Н. Моделирование тепло- и массопереноса в многослойных тепло- и огнезащитных покрытиях при взаимодействии с потоком высокотемпературного газа / Г.Н. Исаков, А.Я. Кузин // Физика горения и взрыва, 1998. –Т.34, №2. –С. 82-89.
Меркулова Н.Н. Методы приближенных вычислений: учебное пособие / Н.Н. Меркулова, М.Д. Михайлов. –2-е изд. –Томск: ТГУ, 2014. –764 с.
Самарский А. А. Теория разностных схем / А. А. Самарский. – Изд-во М., 1977. – 656 с.
Самарский А. А. Вычислительная теплопередача / А. А. Самарский, П. Н. Вабищевич. Изд-во М.: Едиториал УРСС, 2003. – 784 с.
Кузнецов Г. В. Разностные методы задач теплопроводности / Г. В. Кузнецов, М. А. Шеремет. – Изд-во Том. политех. ун-та, 2007. – 172 с.
Кольцова Э.М. Численные методы решения задач в химии и химической технологии: учеб. –метод. пособие. / Э.М. Кольцова, Л.С. Гордеев, А.С Скичко, А.В. Женса // Методы численного решения дифференциальных уравнений на основе разностных схем, 2005.