Дискретные случайные процессы (тема 7)

Тема 7. Дискретные случайные процессы
7. Дискретные случайные процессы
7.1. О характеристиках случайных величин
7.2. О характеристиках случайных процессов
7.3. Преобразование случайного стационарного процесса линейной непрерывной системой
7.4. Преобразование случайного стационарного процесса линейной дискретной системой
7.5. О спектральной факторизации
7.6. Методы определения спектральной плотности дискретного случайного процесса

7.6. Методы определения спектральной плотности дискретного случайного процесса
О классических методах спектрального оценивания
Существует два метода определения спектральной плотности мощности (СПМ):
- прямой метод основан на вычислении квадрата модуля преобразования Фурье для бесконечной последовательности данных с использованием соответствующего статистического усреднения;
- косвенный метод основан на использовании бесконечной последовательности значений данных для расчета автокорреляционной последовательности, преобразования Фурье которой дает искомую спектральную плотность мощности.

Методы определения спектральной плотности дискретного случайного процесса
О методе периодограмм
Рассмотрим практические способы вычисления спектральной плотности дискретного случайного процесса. Напомним, что спектральную плотность можно определить как преобразование Фурье от корреляционной функции Rx[m] дискретного случайного процесса (косвенный метод)
Другой путь определения спектральной плотности - это осреднение спектров реализаций (прямой метод). Этот другой путь перспективен, так как известна эффективность БПФ при вычислении спектров. Напомним, что для реализации x1(t) непрерывного случайного процесса со спектром

Методы определения спектральной плотности дискретного случайного процесса
после усреднения выражения
по всем реализациям получаем
Видим, что спектральная плотность непрерывного случайного процесса пропорциональна среднеквадратичному значению квадратов случайных амплитуд гармоник случайного процесса с частотами, близкими к ω.
Спектр Fx(jω) реализации x[k] дискретного случайного процесса равен

Методы определения спектральной плотности дискретного случайного процесса
По аналогии с приведенным выше выражением для спектральной плотности Sx(ω) непрерывного случайного процесса, полученной путем усреднения по всем реализациям случайного процесса,
мы получим выражение для спектральной плотности дискретного случайного процесса путем усреднения по одной реализации
Так полученная спектральная плотность называется периодограммой.

Методы определения спектральной плотности дискретного случайного процесса
Если значения случайного процесса в начале и конце обрабатываемого отрезка не совпадают, возникает эффект растекания спектра. Дело в том, что БПФ обрабатывает случайный процесс, предполагая его периодическим. Несовпадение значений случайного процесса в начале и в конце эквивалентно разрыву непрерывности. Это вызывает появление высоких частот в спектре, он становится шире – «растекается». Для борьбы с растеканием спектра и по ряду других причин при определении спектра используют окна, отсчеты которых обозначим w[k] . Вычисление идет в этом случае по формуле
Так вычисленная спектральная плотность называется модифицированной периодограммой.

Методы определения спектральной плотности дискретного случайного процесса
В пакете MATLAB вычисление периодограммы проводится с помощью следующей команды
[Sx,f] = periodogram[x,, Nfft, fs...]
Здесь наиболее важные параметры:
x – вектор отсчетов случайного процесса (обязательный параметр),
w– вектор коэффициентов окна,
Nfft - размерность БПФ,
fs - частота дискретизации в герцах,
Sx - вычисленная спектральная плотность,
f - значения частоты, на которых вычислялась спектральная плотность.

Методы определения спектральной плотности дискретного случайного процесса
О методе Уэлча
Периодограмма как результат работы БПФ сильно изрезана, поскольку каждый случайный отсчет входит в обработку и отображается в результате. Для уменьшения изрезанности можно применить усреднение. Так можно в качестве сигнала для обработки использовать значения полусумм соседних отсчетов (метод Даниела). Можно разбить интервал обработки на отрезки, равные интервалу корреляции, и периодограммы отрезков усреднить (метод Бартлета).

Методы определения спектральной плотности дискретного случайного процесса
Уэлч внес две модификации в эти методы обработки:
1. Использовал весовые функции для уменьшения растекания спектра, которое усиливается при разрезании интервала обработки на отрезки.
2. Использовал перекрытие сегментов, когда начало следующего отрезка находится не в конце, а в середине предыдущего отрезка. При этом увеличивается количество отрезков, количество периодограмм, подлежащих усреднению, и повышается точность. С другой стороны, в обработке участвуют коррелированные отсчеты, что понижает точность.
На практике величину перекрытия выбирают около 50%. В MATLABе метод Уэлча реализуется функцией pwelch.

Методы определения спектральной плотности дискретного случайного процесса
О параметрических методах
Среди возможных параметрических методов спектрального анализа наибольшее распространение получили методы, основанные на авторегрессионной модели формирования сигнала. Эта модель предполагает, что анализируемый сигнал x[n] можно представить в виде выхода фильтра, на вход которого подан белый шум g[n].
Уравнение авторегрессионного фильтра имеет вид
или

Методы определения спектральной плотности дискретного случайного процесса
Если все коэффициенты фильтра ai известны, и известна дисперсия входного белого шума σg2, то спектральная плотность выхода вычисляется по формуле:
Постановка задачи
Предположим, что x[n] является выходом фильтра, но коэффициенты фильтра неизвестны.
Покажем, что тогда можно с помощью адаптивного фильтра найти эти коэффициенты.
Конец постановки задачи

Методы определения спектральной плотности дискретного случайного процесса
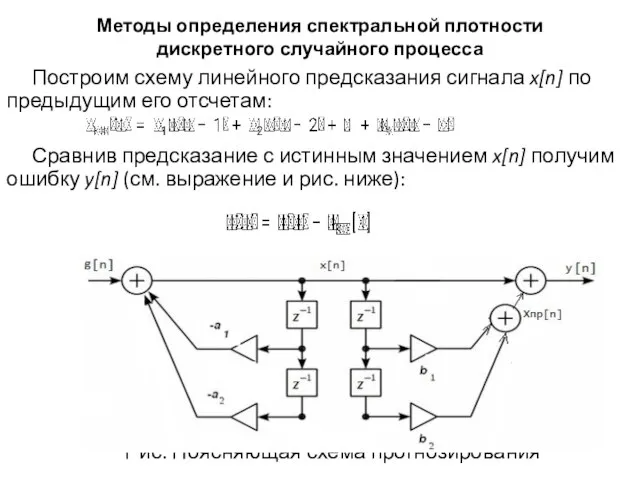
Построим схему линейного предсказания сигнала x[n] по предыдущим его отсчетам:
Сравнив предсказание с истинным значением x[n] получим ошибку y[n] (см. выражение и рис. ниже):
Рис. Поясняющая схема прогнозирования

Методы определения спектральной плотности дискретного случайного процесса
Для Z– преобразования ошибки из рис. выше следует:
Разложим дробь в ряд, получим:
Тогда выражение для ошибки можно записать:
Поскольку отсчеты белого шума независимы, то для дисперсии ошибки получим

Методы определения спектральной плотности дискретного случайного процесса
Минимальное значение дисперсии ошибки σy2 можно получить, если все γi = 0. Тогда из приведенного ранее выражения
Следует
bi = ai
Следовательно, если минимизировать ошибку y[n], то bi дадут оценку коэффициентов ai неизвестного фильтра. Определив коэффициенты вычисляем спектральную плотность по соотношению