Двухполюсник в цепи синусоидальноrо тока

Частотные xapaктepистики (ЧХ) двухполюсника: зависимость модуля входного сопротивления (проводимости) от частоты; зависимость действительной или мнимой части входного сопротивления (проводимости ) от частоты.
Резонансный режим (режимы) работы при котором входное сопротивление двухполюсника чисто активное. По отношению к внешней цепи двухполюсник в резонансном режиме ведёт себя .как активное сопротивление, ток и нaпряжение на ero входе совпадают по фазе, реактивная мощность двухполюсника равна нулю. Цепи, в которых возникает явление резонанса, наз. резонансными, могут наблюдаться резонанс токов, резонанс напряжений.
Мощности цепи синусоидального тока:
Мгновенная
В
В
Активная
реактивная

Резонанс в электрических цепях
- режим работы электрической цепи, содержащей индуктивные и ёмкостные элементы, при котором
входное сопротивление цепи имеет чисто активный характер и, следовательно, сдвиг фаз между напряжением и током на ее входе равен нулю (φ = 0).
Разнородные реактивные сопротивления (проводимости) цепи полностью компенсируют друг друга. Полная реактивная мощность Q цепи при этом равна нулю.
Цепи, в которых возникают резонансные явления, называют резонансными цепями или колебательными контурами.
Различают : резонанс напряжений (в цепях или колебательных контурах с последовательным соединением ветвей, содержащих L и C элементы) и резонанс токов (в цепях или колебательных контурах с параллельным соединением ветвей, содержащих L и C элементы).
В электротехнических установках резонанс часто оказывается опасным и нежелательным явлением, так как может привести к авариям вследствие перегрева элементов электрической цепи или пробоя изоляции при перенапряжениях.
Тем не менее, резонансные явления широко применяют в радиоэлектронике. Резонансные контуры входят в состав многих радиотехнических устройств, электронные фильтры являются сложными резонансными системами.

Признаки резонанса напряжений:
Напряжение на входе совпадает по фазе с током, т.е. сдвиг фаз между I
и U φ=0, cos(φ)=1
2. Ток в цепи наибольший и, как следствие, активная мощность Pmax=I2maxR максимальна, а реактивная - равна нулю.
3. Напряжения на реактивных элементах цепи могут в несколько раз превышать напряжение на входе.
4.
Простейшая цепь, где возможен резонанс напряжений, - последовательный колебательный контур. Режим работы RLC цепи, при условии равенства реактивных сопротивлений XC=XL, когда общее напряжение цепи совпадает по фазе с её током φ=0, наз. резонансом напряжений. Цепь имеет активный характер:
Резонанс напряжений

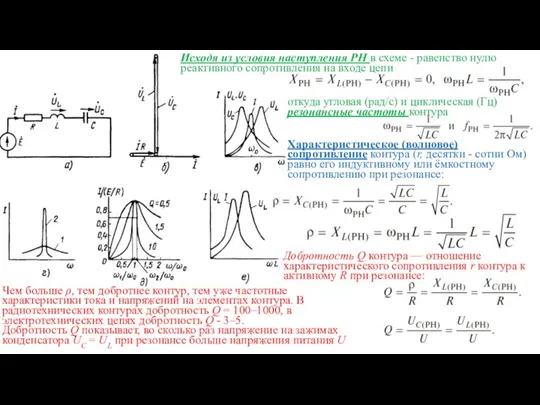
Исходя из условия наступления РН в схеме - равенство нулю реактивного сопротивления на входе цепи
откуда угловая (рад/с) и циклическая (Гц) резонансные частоты контура
Характеристическое (волновое) сопротивление контура (r, десятки - сотни Ом) равно его индуктивному или ёмкостному сопротивлению при резонансе:
Добротность Q контура — отношение характеристического сопротивления r контура к активному R при резонансе:
Чем больше ρ, тем добротнее контур, тем уже частотные характеристики тока и напряжений на элементах контура. В радиотехнических контурах добротность Q = 100–1000, в электротехнических цепях добротность Q - 3–5.
Добротность Q показывает, во сколько раз напряжение на зажимах конденсатора UC = UL при резонансе больше напряжения питания U

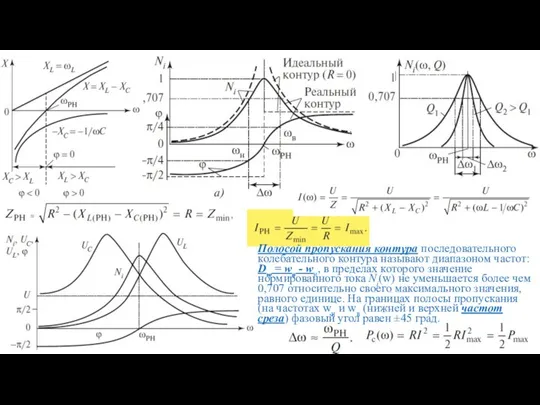
Полосой пропускания контура последовательного колебательного контура называют диапазоном частот: Dw = wв - wн, в пределах которого значение нормированного тока Ni(w) не уменьшается более чем 0,707 относительно своего максимального значения, равного единице. На границах полосы пропускания (на частотах wн и wв (нижней и верхней частот среза) фазовый угол равен ±45 град.

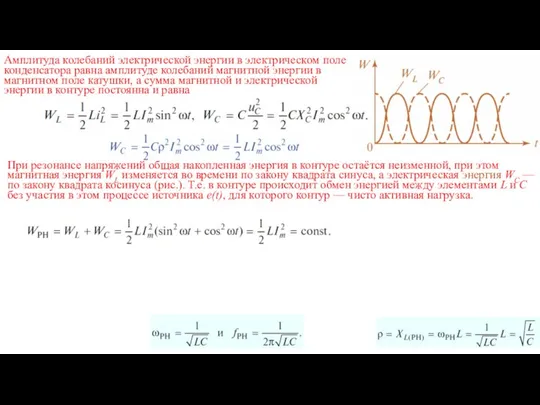
При резонансе напряжений общая накопленная энергия в контуре остаётся неизменной, при этом магнитная энергия WL изменяется во времени по закону квадрата синуса, а электрическая энергия WC — по закону квадрата косинуса (рис.). Т.е. в контуре происходит обмен энергией между элементами L и C без участия в этом процессе источника е(t), для которого контур — чисто активная нагрузка.
Амплитуда колебаний электрической энергии в электрическом поле конденсатора равна амплитуде колебаний магнитной энергии в магнитном поле катушки, а сумма магнитной и электрической энергии в контуре постоянна и равна

РЕЗОНАНС ТОКОВ
Резонанс токов (РТ) возникает в параллельном колебательном контуре при равенство нулю входной реактивной
проводимости bPT = bL(PT) – bC (PT) = 0 или
Резонансная угловая частота
где - резонансная частота
контура без потерь (R1 = R2 = 0);
- характеристическое сопротивление контура.
В частном случае при R2 = 0
когда R2 = 0 и R1 << wL, резонанс наступает при
Т.к. резонансная частота — действительна и положительна, то при
режим резонанса невозможен.
такой режим возможен при

Резонансные свойства цепи с двумя ветвями R1L и R2C удобно изучать на эквивалентной схеме замещения с тре­мя параллельно соединёнными ветвями с параметрами g, bL и bC, равными
Добротность Q параллельного колебатель­ного контура равна
либо отношению тока IС в ветви с конденсатором (при R2 = 0) при режиме РТ и тока IРТ на зажимах контура
Ток I при РТ минимален
Амплитудно-частотная характеристика (АЧХ) тока I(f) и фазо-частот­ная ха­рак­теристика (ФЧХ) ϕ(f) реального и идеального контуров

Параллельное соединение элементов в цепях синусоидального тока

Треугольники проводимостей
G – действительная часть, активная составляющая
B – мнимая часть, реактивная составляющая

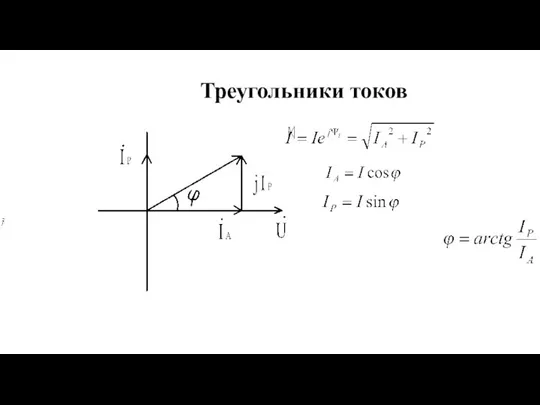
Треугольники токов

Резонанс токов
Режим токов при котором в цепи, содержащей параллельные ветви с индуктивными и емкостными элементами, ток неразветвленного участка цепи совпадает по фазе с напряжением (φ=0), называют резонансом токов.
Условие резонанса токов:
Равенство реактивных составляющих проводимостей в ветвях

Признаки резонанса токов
Токи ветвей равны IPC=IPL и находятся в противофазе.
Токи ветвей превышают полный ток цепи, который имеет минимальное значение.
и совпадают по фазе, φ= 0

Частотные характеристики цепей синусоидального тока
R – активное сопротивление не зависит от частоты
XL,XC – реактивные сопротивления зависят от частоты
На графиках показаны зависимости тока, полного комплексного сопротивления и угла сдвига фаз от частоты

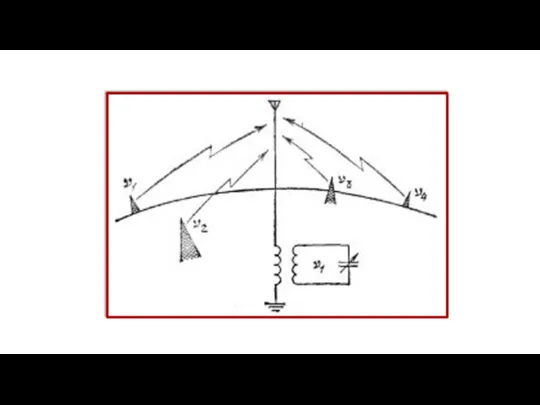
Применение электрического резонанса

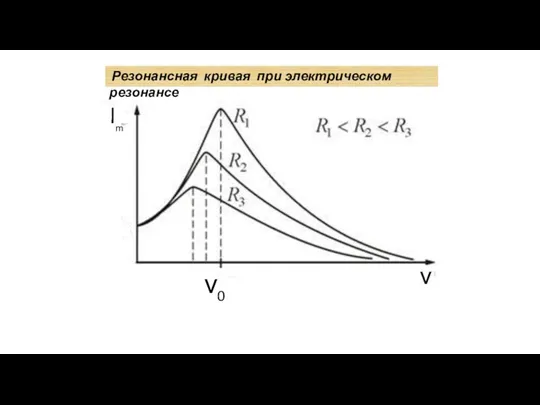
I
m
ν
ν
0
Резонансная кривая при электрическом резонансе

Емкость конденсатора можно плавно изменять, меняя тем самым собственную частоту контура. Если мы настроим контур на желательную частоту, например n1, то э. д. с. с частотой n1 вызовет в контуре сильные вынужденные колебания, а все остальные э. д. с.— слабые. Следовательно,

Из этого графика видно, что в течение одной четверти периода мощность положительна и энергия от сети поступает к данному участку цепи; но в течение следующей четверти периода мощность отрицательна, и данный участок отдает без потерь обратно в сеть полученную ранее энергию. Поступающая в течение четверти периода энергия запасается в магнитном поле тока, а затем без потерь возвращается в сеть
Лишь при наличии проводника с активным сопротивлением в цепи, электромагнитная энергия превращается во внутреннюю энергию проводника, который нагревается. Обратного превращения внутренней энергии в электромагнитную на участке с активным сопротивлением уже не происходит, энергия в сеть не возвращается.
График колебаний мощности
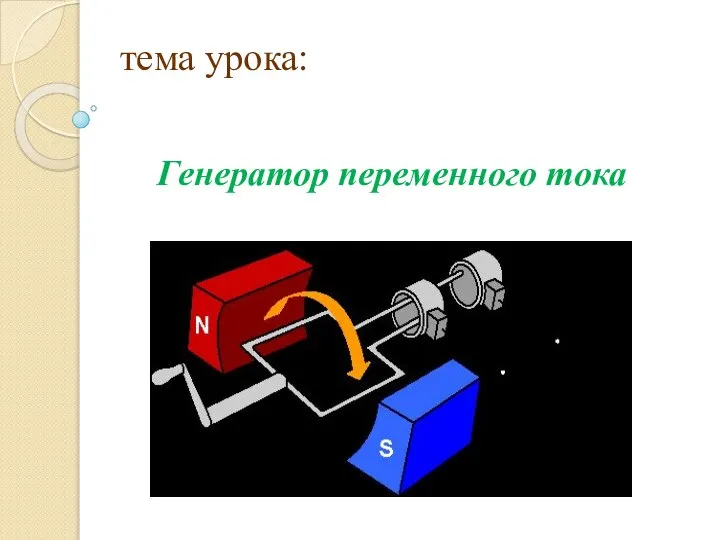при наличии в цепи переменного тока только индуктивного сопротив-
ления.