Слайд 2§15. Механические колебания
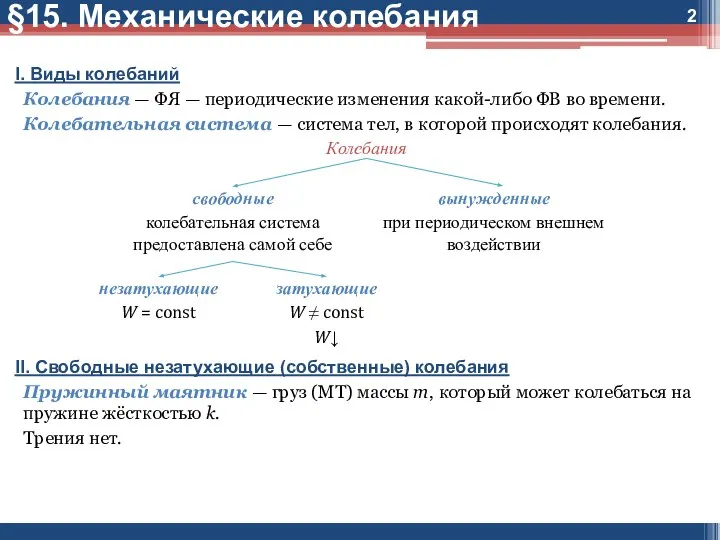
I. Виды колебаний
Колебания — ФЯ — периодические изменения какой-либо ФВ
во времени.
Колебательная система — система тел, в которой происходят колебания.
II. Свободные незатухающие (собственные) колебания
Пружинный маятник — груз (МТ) массы m, который может колебаться на пружине жёсткостью k.
Трения нет.
Слайд 3§15. Механические колебания
II закон Ньютона:
— дифференциальное уравнение свободных гармонических колебаний
Общее решение: —

гармоническая функция
Подставим начальные условия: при t = 0 x = x0, vx = 0
Частное решение:
Слайд 5§15. Механические колебания
A — амплитуда колебаний — максимальное отклонение колеблющейся величины от

равновесного значения.
ω0 — ФВ — циклическая частота
Выражение в скобках — фаза колебаний
φ — начальная фаза
Период T0 — ФВ — время, за которое колебательная система совершает одно полное колебание.
Частота ν0 — ФВ — число полных колебаний в единичный промежуток времени.
Энергия колебаний (механическая энергия колебательной системы):
Слайд 6§15. Механические колебания
Примеры
1. Математический маятник
Математический маятник — МТ, подвешенная на невесомой нерастяжимой

нити в однородном гравитационном поле.
II закон Ньютона:
(закон всемирного тяготения)
При малых углах sin φ ≈ φ
Слайд 7§15. Механические колебания
2. Физический маятник
Физический маятник — ТТ, которое может вращаться вокруг

неподвижной горизонтальной оси, проходящей через точки этого тела, не являющиеся его ЦМ, в однородном гравитационном поле.
ОУДВД:
(закон всемирного тяготения)
При малых углах sin φ ≈ φ
Слайд 8§15. Механические колебания
III. Свободные затухающие колебания
Рассмотрим пружинный маятник.
Сила вязкого трения
II закон

Ньютона:
β — коэффициент затухания
— дифференциальное уравнение свободных затухающих колебаний
Слайд 9§15. Механические колебания
1. Сильное затухание (β ≥ ω0)
Общее решение: — апериодическое решение
2. Слабое
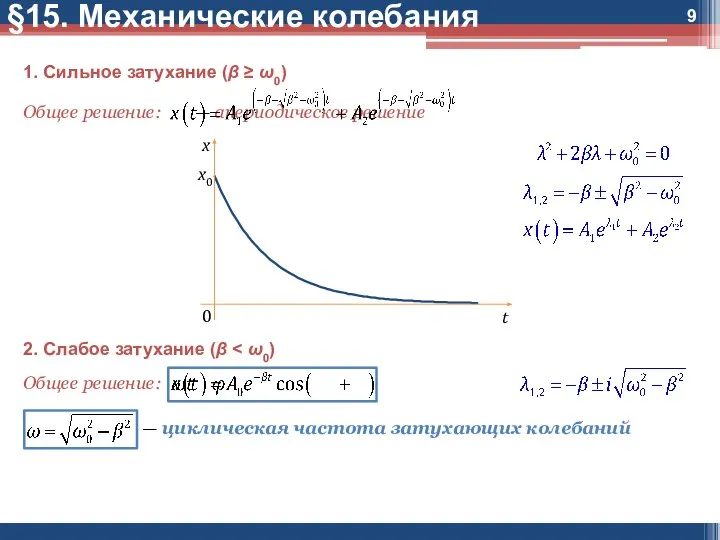
затухание (β < ω0)
Общее решение:
— циклическая частота затухающих колебаний
Слайд 10§15. Механические колебания
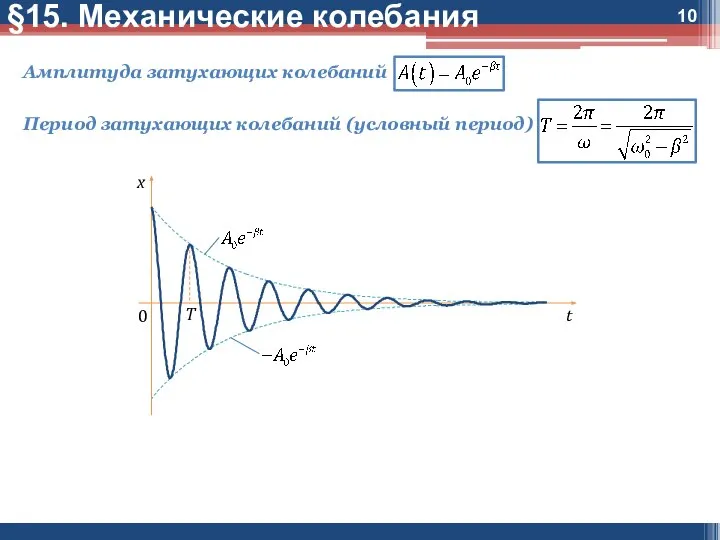
Амплитуда затухающих колебаний
Период затухающих колебаний (условный период)
Слайд 11§15. Механические колебания
IV. Вынужденные колебания
Рассмотрим пружинный маятник, находящийся под воздействием, описываемым периодической

силой
II закон Ньютона:
— дифференциальное уравнение вынужденных гармонических колебаний
Общее решение (при β < ω0):
Слайд 12§15. Механические колебания
x1(t) быстро затухает → циклическая частота вынужденных колебаний равна Ω

Слайд 13§15. Механические колебания
Ωmin = 0
— резонансная циклическая частота
Резонанс — ФЯ — резкое возрастание амплитуды

вынужденных колебаний при приближении циклической частоты вынуждающей силы к резонансной циклической частоте.











 И. Кеплер, и его вклад и развитие механики
И. Кеплер, и его вклад и развитие механики Электрический ток в вакууме
Электрический ток в вакууме Механическая работа. Мощность
Механическая работа. Мощность Свет и цвет. Естествознание, 10 класс
Свет и цвет. Естествознание, 10 класс Электроосветительные установки
Электроосветительные установки Электризация тел при соприкосновении. Два рода зарядов
Электризация тел при соприкосновении. Два рода зарядов Скорость
Скорость Первый закон термодинамики. Необратимость процессов в природе
Первый закон термодинамики. Необратимость процессов в природе Техническое обслуживание и ремонт двигателей, систем и агрегатов автомобилей
Техническое обслуживание и ремонт двигателей, систем и агрегатов автомобилей Атом (по Демокриту) – простейшая, неделимая далее частица
Атом (по Демокриту) – простейшая, неделимая далее частица Тематический состав ВсОШ по физике для 9-ого класса
Тематический состав ВсОШ по физике для 9-ого класса Взаимодействие тел. Сила. Противодействие
Взаимодействие тел. Сила. Противодействие Движение по окружности
Движение по окружности Расчёт аэродинамических характеристик самолётов
Расчёт аэродинамических характеристик самолётов Единицы измерения скорости. Формула скорости
Единицы измерения скорости. Формула скорости Технология компрессии изображений Smart Compression of Images
Технология компрессии изображений Smart Compression of Images Энергия связи
Энергия связи Разметчик Фибоначчи
Разметчик Фибоначчи Модель атома Томсона
Модель атома Томсона Звуковые волны
Звуковые волны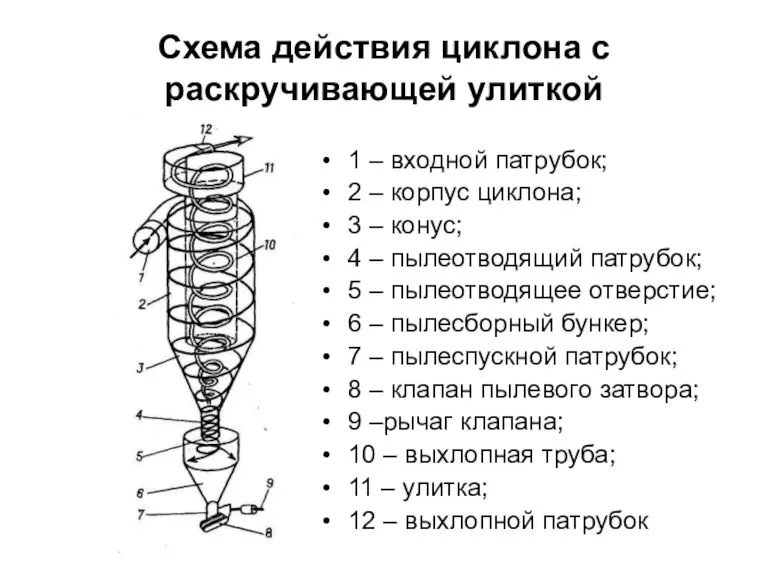 Схема действия циклона с раскручивающей улиткой
Схема действия циклона с раскручивающей улиткой Мобильный микроманипулятор для экстремальных климатических условий
Мобильный микроманипулятор для экстремальных климатических условий Барометр-анероид
Барометр-анероид Линзы. Оптическая сила линзы
Линзы. Оптическая сила линзы Качество деталей машин. Качество материалов
Качество деталей машин. Качество материалов Электрические цепи. Тема 11
Электрические цепи. Тема 11 Основное положение МКТ
Основное положение МКТ Учимся мыслить
Учимся мыслить