Содержание
- 2. Магнитное поле Магнетит (от античного города Магнесия в Малой Азии) Fe3O4 – природный минерал с сильными
- 3. Первое серьезное исследование электрических и магнитных явлений выполнил William Gilbert (1544-1603) в Англии. В 1600 году
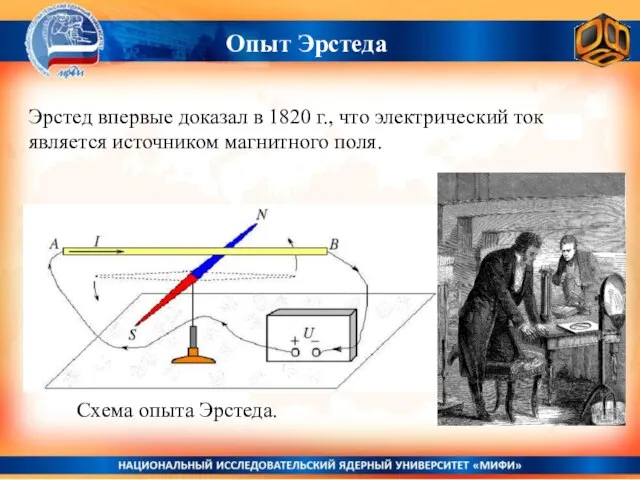
- 4. Эрстед впервые доказал в 1820 г., что электрический ток является источником магнитного поля. Схема опыта Эрстеда.
- 5. Свойства магнитного поля Опыт показывает, что Магнитное поле создаётся движущимися электрическими зарядами (электротоком); Магнитное поле действует
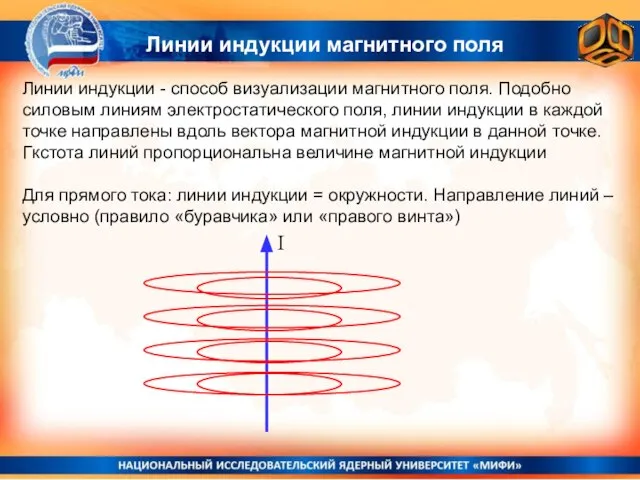
- 6. Линии индукции магнитного поля Линии индукции - способ визуализации магнитного поля. Подобно силовым линиям электростатического поля,
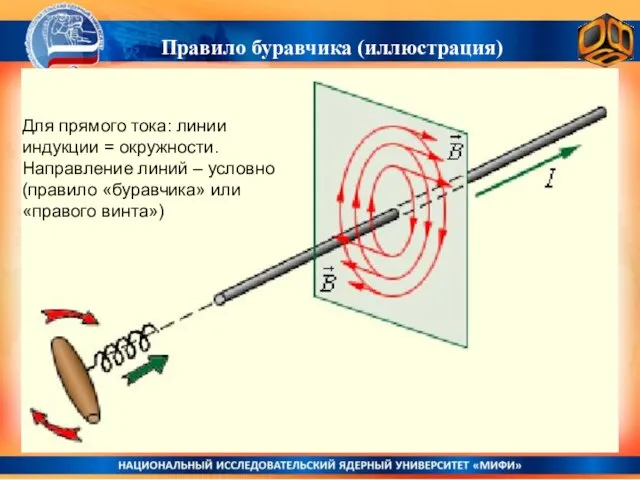
- 7. Правило буравчика (иллюстрация) Для прямого тока: линии индукции = окружности. Направление линий – условно (правило «буравчика»
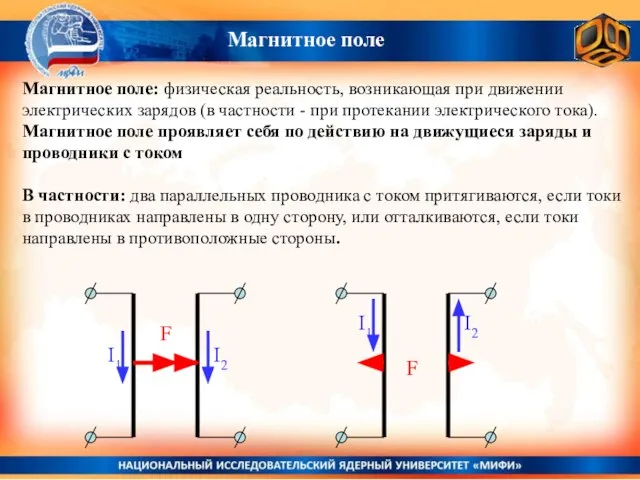
- 8. Магнитное поле Магнитное поле: физическая реальность, возникающая при движении электрических зарядов (в частности - при протекании
- 9. Магнитное поле (1) Магнитное поле создаётся движущимися электрическими зарядами: Закон Био – Савара –Лапласа
- 10. Закон Био – Савара - Лапласа Магнитное поле равномерно движущегося заряда Гн = Н·м/А2
- 11. Магнитное поле постоянного тока Магнитостатика изучает постоянные, т.е. независящие от времени магнитные поля, создаваемые постоянными токами.
- 12. Закон Био – Савара - Лапласа Био – Савар (1820, эксперимент) Лаплас (1826, теория)
- 13. Закон Био – Савара для линейного проводника с током Закон Био – Савара - Лапласа
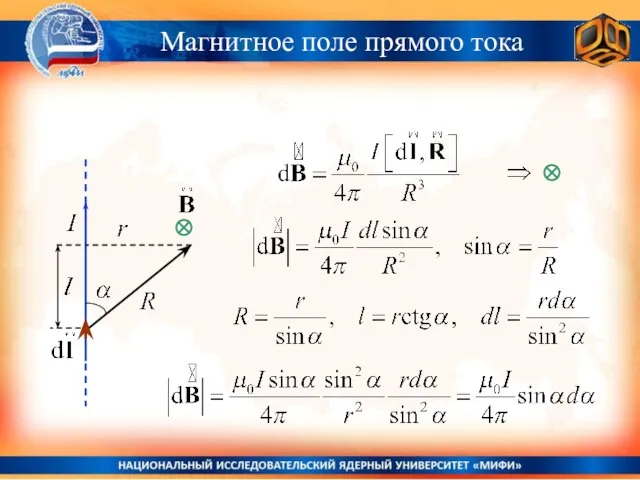
- 14. Магнитное поле прямого тока
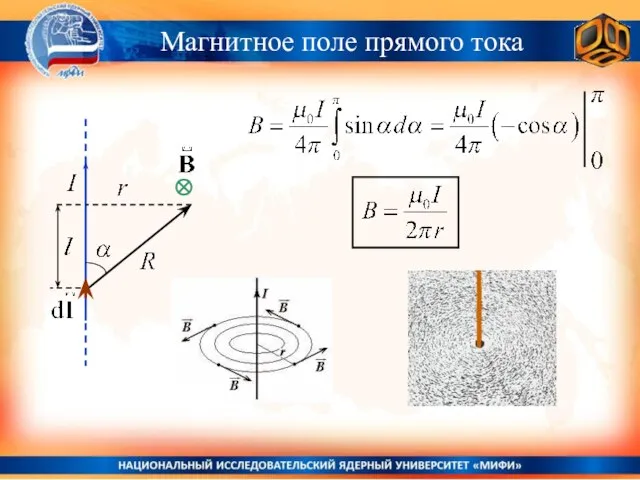
- 15. Магнитное поле прямого тока
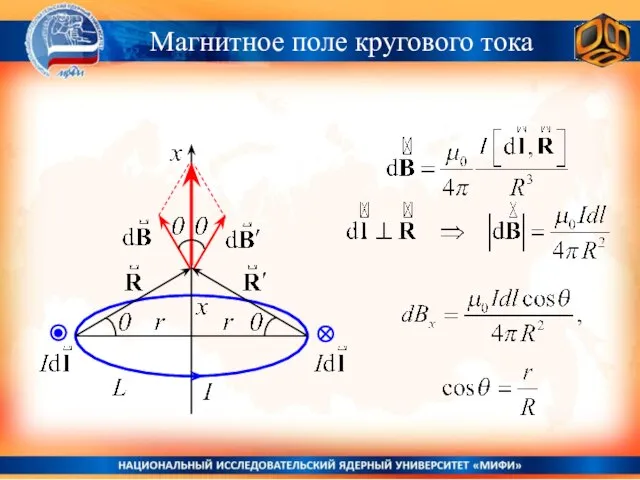
- 16. Магнитное поле кругового тока
- 17. Магнитное поле кругового тока
- 18. Магнитное поле соленоида (катушки с током) Каждый виток катушки создает в центре соленоида магнитное поле с
- 19. Пример решения задач Пример 1. Постоянный ток I протекает по двум полубесконечным прямым проводникам, соединённым между
- 20. Магнитное поле (2) Магнитное поле действует на движущиеся заряды Сила Лоренца Закон Ампера
- 21. Сила Лоренца Магнитная сила
- 22. Магнитное поле действует на движущийся заряд q с силой в направлении, перпендикулярном его скорости V и
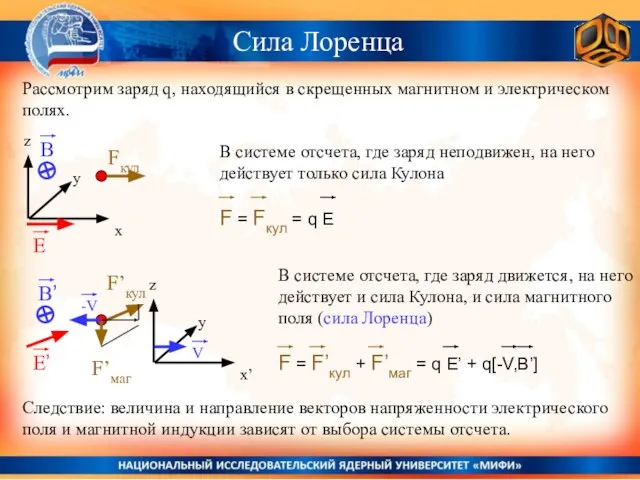
- 23. Рассмотрим заряд q, находящийся в скрещенных магнитном и электрическом полях. Fкул B y x z E
- 24. Сила Лоренца Сила Лоренца Разделение силы Лоренца на электрическую и магнитную составляющие зависит от системы отсчёта.
- 25. Закон Ампера Магнитная сила, действующая на проводник с током
- 26. Андре́-Мари́ Ампе́р 1775-1836 Закон Ампера Закон Ампера для линейного проводника
- 27. Закон Ампера Сила магнитного взаимодействия двух параллельных линейных бесконечных токов в вакууме
- 28. Закон Ампера Единица силы тока в системе СИ Прохождение тока силой в 1 Ампер по двум
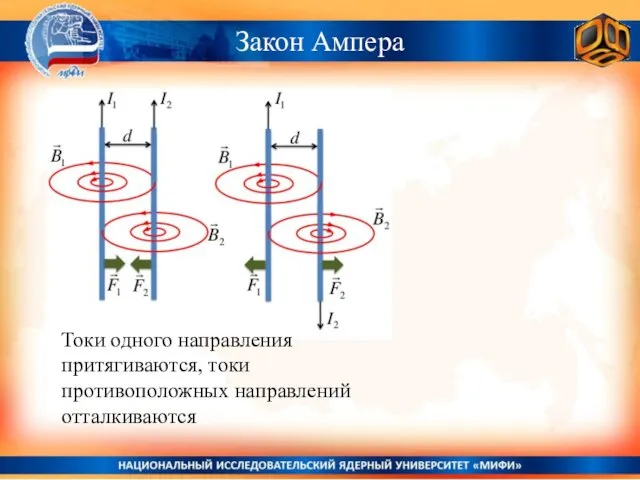
- 29. Закон Ампера Токи одного направления притягиваются, токи противоположных направлений отталкиваются
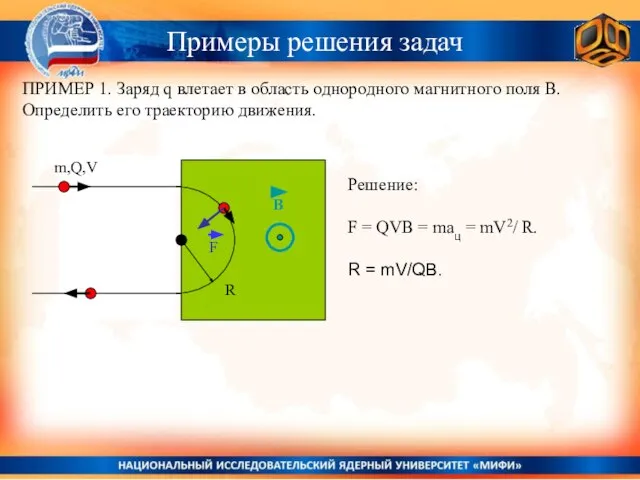
- 30. ПРИМЕР 1. Заряд q влетает в область однородного магнитного поля В. Определить его траекторию движения. m,Q,V
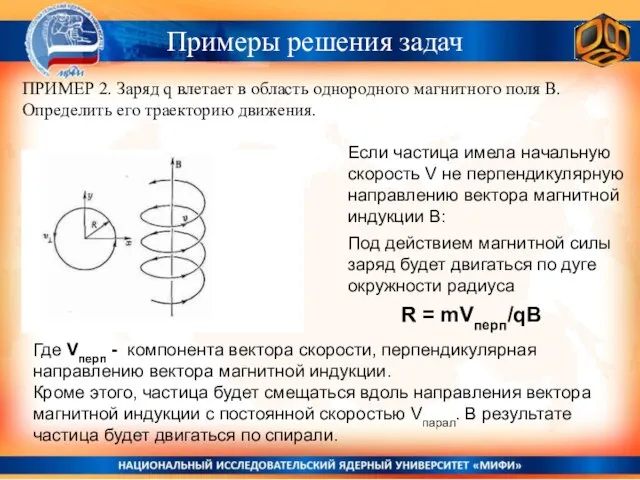
- 31. Если частица имела начальную скорость V не перпендикулярную направлению вектора магнитной индукции В: Под действием магнитной
- 32. Примеры решения задач
- 33. Примеры решения задач
- 34. Спасибо за внимание! Курс общей физики НИЯУ МИФИ Следующая лекция 3 ноября
- 36. Скачать презентацию






















 Давление газа
Давление газа Презентация на тему Условия плавания тел
Презентация на тему Условия плавания тел  Электрические цепи
Электрические цепи Приложения криволинейных интегралов в геометрии и механике
Приложения криволинейных интегралов в геометрии и механике Презентация на тему Кроссворд
Презентация на тему Кроссворд  Разработка способа производства радиоизотопов Скандия на Циклотроне ФТИ УрФУ
Разработка способа производства радиоизотопов Скандия на Циклотроне ФТИ УрФУ Приймачі світла
Приймачі світла Техническое обслуживание и текущий ремонт сцепления, коробки передач, карданной передачи
Техническое обслуживание и текущий ремонт сцепления, коробки передач, карданной передачи Technical Service Bulletin. Модель Mighty. Замена клапана ЕГР
Technical Service Bulletin. Модель Mighty. Замена клапана ЕГР Переменный ток. Действующие значения тока и напряжения
Переменный ток. Действующие значения тока и напряжения Вес воздуха. Атмосферное давление
Вес воздуха. Атмосферное давление Модель машины
Модель машины Задачи атомной и ядерной физики, астрономии
Задачи атомной и ядерной физики, астрономии Виды зубчатых передач
Виды зубчатых передач Кинематические характеристики движения
Кинематические характеристики движения Понятие о вакууме
Понятие о вакууме Нанотехнологии и их применение
Нанотехнологии и их применение Закон радиоактивного распада. Решение задач
Закон радиоактивного распада. Решение задач Технология и организация судоремонта
Технология и организация судоремонта Методы, основанные на индуцированном переходе из одной фазы в другую через разделяющую их третью фазу. (Лекция 7)
Методы, основанные на индуцированном переходе из одной фазы в другую через разделяющую их третью фазу. (Лекция 7) Тепловые двигатели. История создания. Устройство. Принцип действия. Коэффициент полезного действия. Применение
Тепловые двигатели. История создания. Устройство. Принцип действия. Коэффициент полезного действия. Применение Законы динамики Ньютона
Законы динамики Ньютона Светодиоды. Применение светодиодов
Светодиоды. Применение светодиодов Давление. Единицы давления
Давление. Единицы давления Распределения молекул по скоростям и энергиям
Распределения молекул по скоростям и энергиям Физические явления. Химические реакции
Физические явления. Химические реакции Изучение хроматографической подвижности
Изучение хроматографической подвижности 1662358633106__vzy6vf
1662358633106__vzy6vf