Содержание
- 2. Мы знаем действия многих причин, но не знаем причин многих действий. К. Колтон Мысли философов –
- 3. Уравнение волны Уравнение волны – математическое выражение, описывающее смещение колеблющейся частицы в виде функции, зависящей от
- 4. Гармоническая волна: А.С. Чуев, 2020
- 5. Уравнение плоской гармонической волны: Уравнение плоской одномерной гармонической волны: Уравнение плоской одномерной затухающей гармонической волны: Уравнение
- 6. дважды продифференцировать по времени и координатам, то получим волновое уравнение второго порядка - волновое число -
- 7. Амплитуда волны на расстоянии l : Плоская волна при х = 0 А.С. Чуев, 2020 где:
- 8. - волновой вектор. - волновое число. А.С. Чуев, 2020 Далее - вывод волнового уравнения из уравнения
- 9. Продифференцируем функцию дважды по каждой переменной А.С. Чуев, 2020
- 10. А.С. Чуев, 2020
- 11. Для одномерной плоской волны волновое уравнение имеет вид: А.С. Чуев, 2020 Запомнить:
- 12. А.С. Чуев, 2020
- 13. Вибратор Герца Вибратор R – разрядник; Т - газоразрядная трубка; D – дроссели. Резонатор Движущийся с
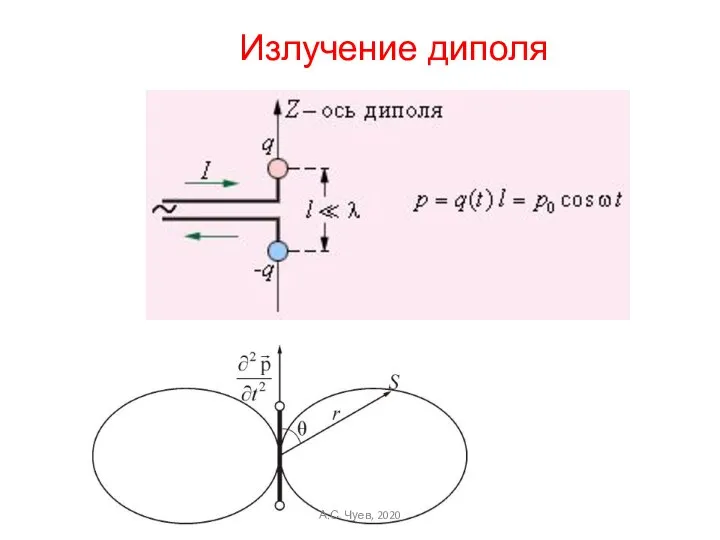
- 14. Излучение диполя А.С. Чуев, 2020
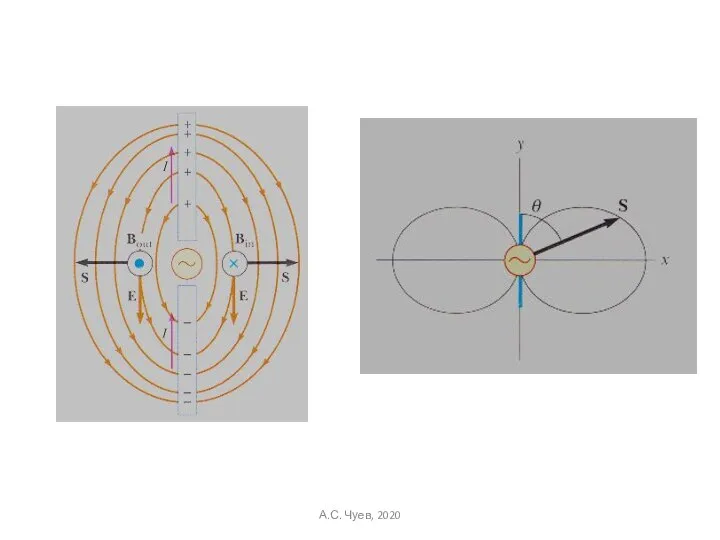
- 15. А.С. Чуев, 2020
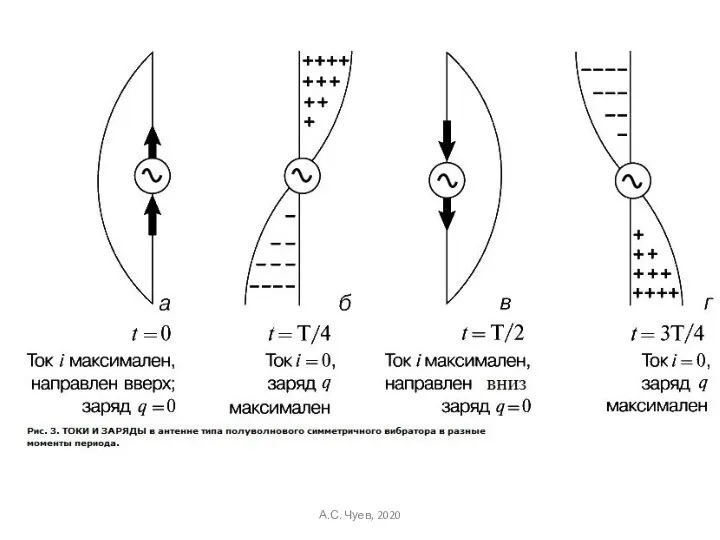
- 16. А.С. Чуев, 2020
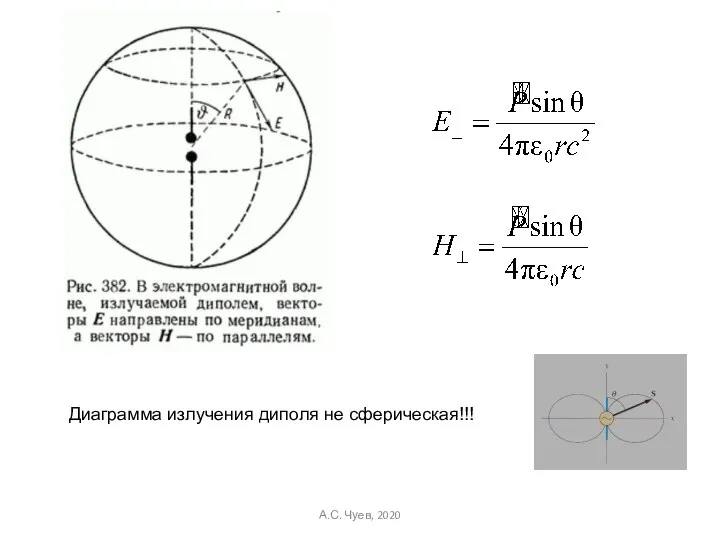
- 17. Диаграмма излучения диполя не сферическая!!! А.С. Чуев, 2020
- 18. ФАР А.С. Чуев, 2020
- 19. А.С. Чуев, 2020
- 20. А.С. Чуев, 2020
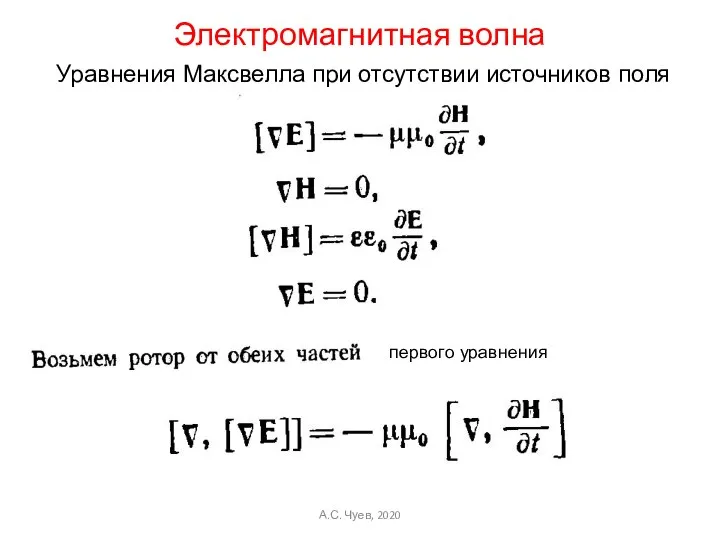
- 21. Уравнения Максвелла при отсутствии источников поля первого уравнения Электромагнитная волна А.С. Чуев, 2020
- 22. Преобразуя векторное произведение в правой части последнего уравнения: И использовав для rot Н, выражение из ур-ий
- 23. Аналогичным путем можно получить А.С. Чуев, 2020
- 24. А.С. Чуев, 2020 Второй вариант вывода волнового уравнения дифференцируем по х дифференцируем по t Исключая из
- 25. где – оператор Лапласа, υ – фазовая скорость. Другой вид волновых формул для электромагнитных волн А.С.
- 26. Еще один вариант записи волновых уравнений для электромагнитных волн А.С. Чуев, 2020
- 27. Уравнения Максвелла можно решить подстановкой: где и обязаны удовлетворять уравнениям: Там, где и равны нулю (в
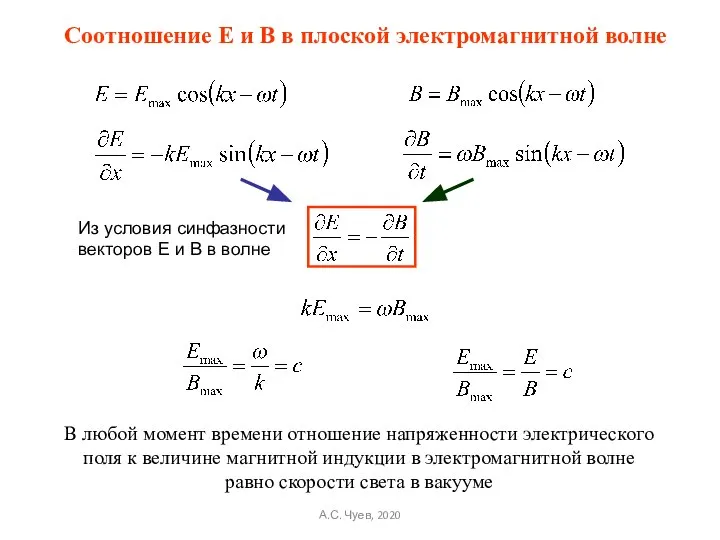
- 28. В любой момент времени отношение напряженности электрического поля к величине магнитной индукции в электромагнитной волне равно
- 29. Скорость распространения электромагнитных волн в среде зависит от ее электрической и магнитной проницаемостей. Величину абсолютным показателем
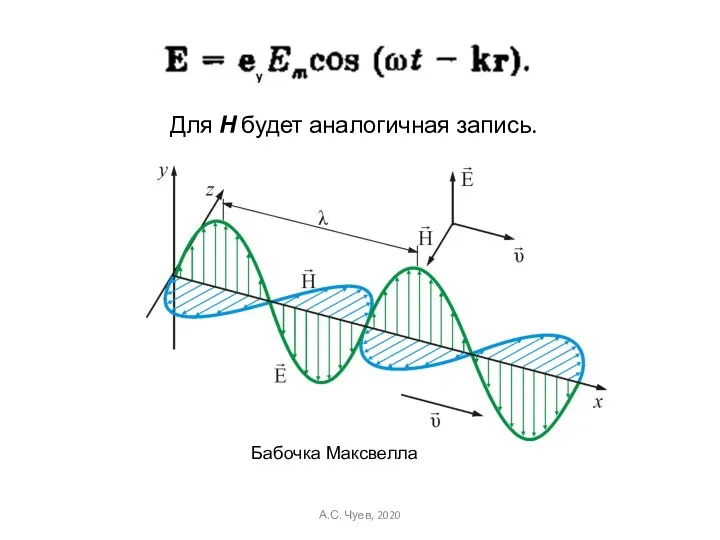
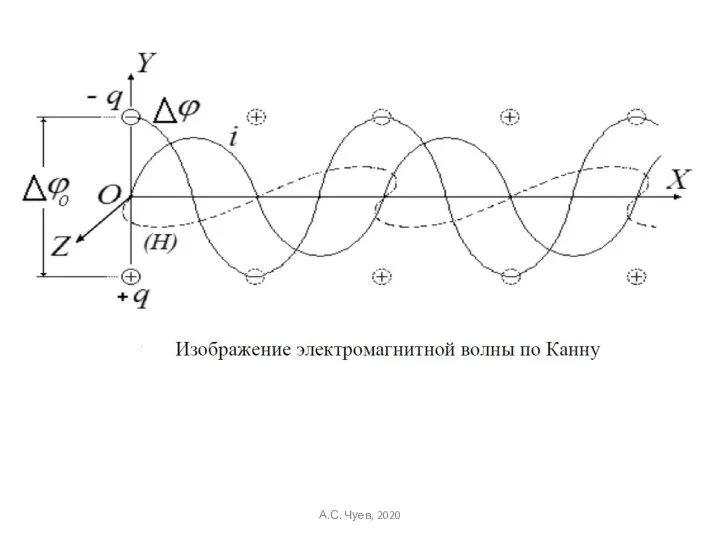
- 30. Изменения Е и Н синфазны!!! Для плоской гармонической волны: Электромагнитные волны – поперечные волны А.С. Чуев,
- 31. Соотношение Е/Н Для вакуума А.С. Чуев, 2020
- 32. Для Н будет аналогичная запись. Бабочка Максвелла А.С. Чуев, 2020
- 33. Уравнение встречной волны: Результат наложения прямой и встречной волн: А.С. Чуев, 2020
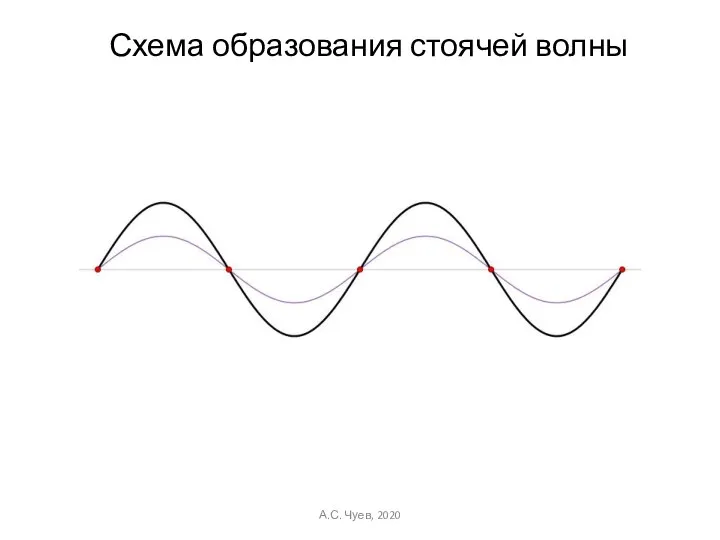
- 34. Схема образования стоячей волны А.С. Чуев, 2020
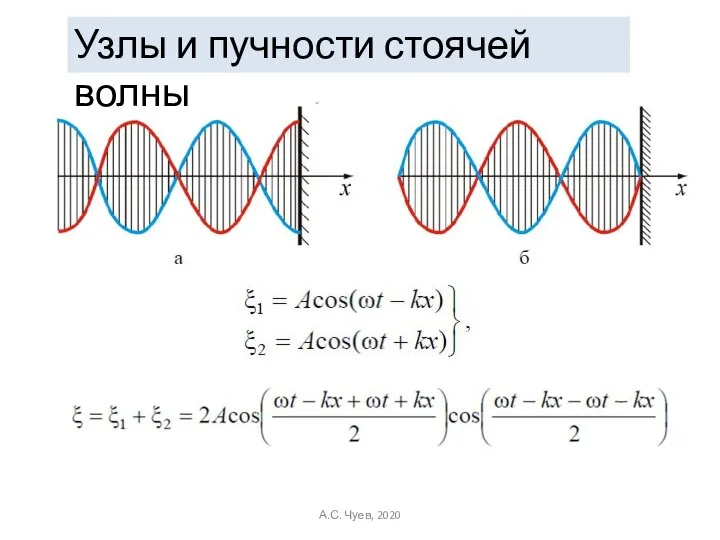
- 35. Узлы и пучности стоячей волны А.С. Чуев, 2020
- 36. С учетом, Уравнение стоячей волны имеет вид: Стоячие волны не переносят энергию !!! А.С. Чуев, 2020
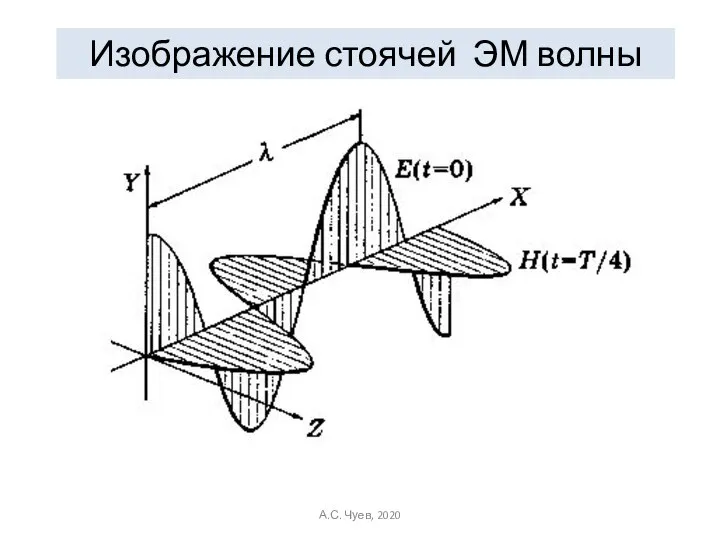
- 37. Изображение стоячей ЭМ волны А.С. Чуев, 2020
- 38. Используя соотношения Е с Н, можно получить А.С. Чуев, 2020
- 39. Квадрат косинуса = 1/2 Интенсивность: В результате: А.С. Чуев, 2020
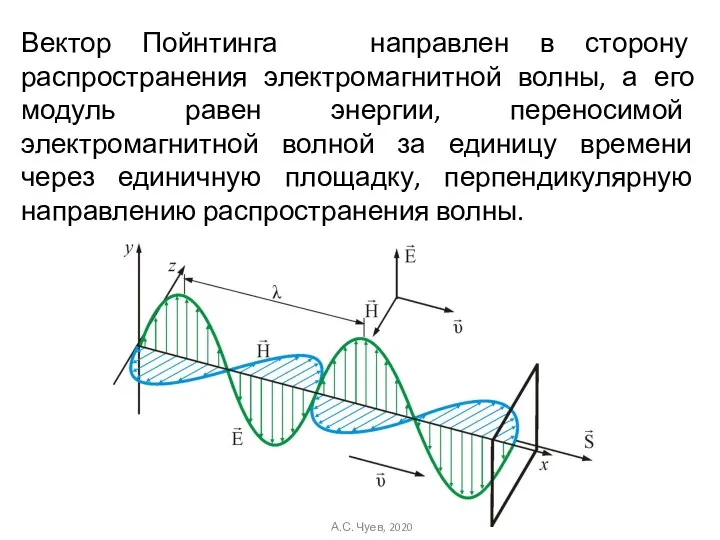
- 40. А.С. Чуев, 2020 Вектор Пойнтинга направлен в сторону распространения электромагнитной волны, а его модуль равен энергии,
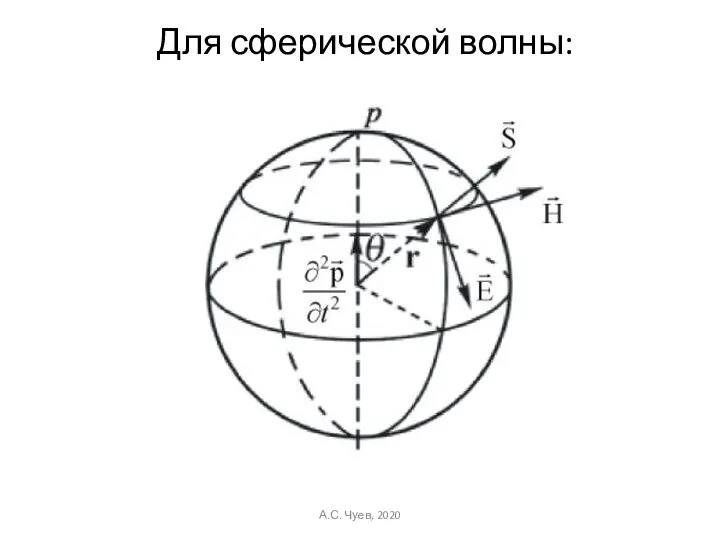
- 41. Для сферической волны: А.С. Чуев, 2020
- 42. Теорема Пойнтинга Используя векторное тождество: Из уравнений Максвелла можно получить: Преобразуем левую часть: и Получим уравнение
- 43. Это уравнение похоже на уравнение непрерывности: Применяя формулу Гаусса-Остроградского уравнение баланса энергии можно выразить в интегральной
- 44. А.С. Чуев, 2020 σ - удельная проводимость
- 45. Импульс электромагнитной волны Умножив числитель и знаменатель на скорость света, получим: А.С. Чуев, 2020
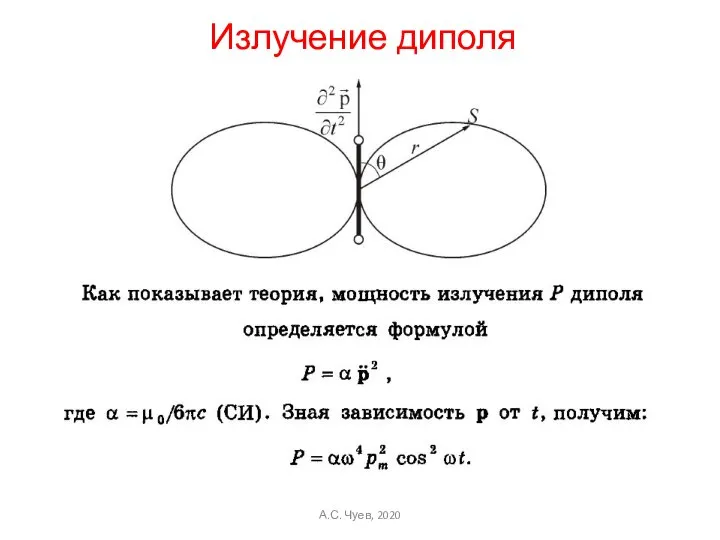
- 46. Излучение диполя А.С. Чуев, 2020
- 47. А.С. Чуев, 2020
- 48. Далее Факультативный материал А.С. Чуев, 2020
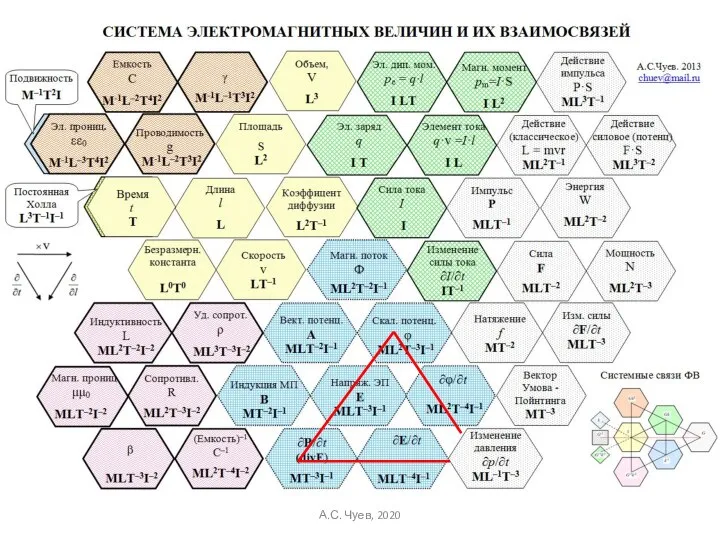
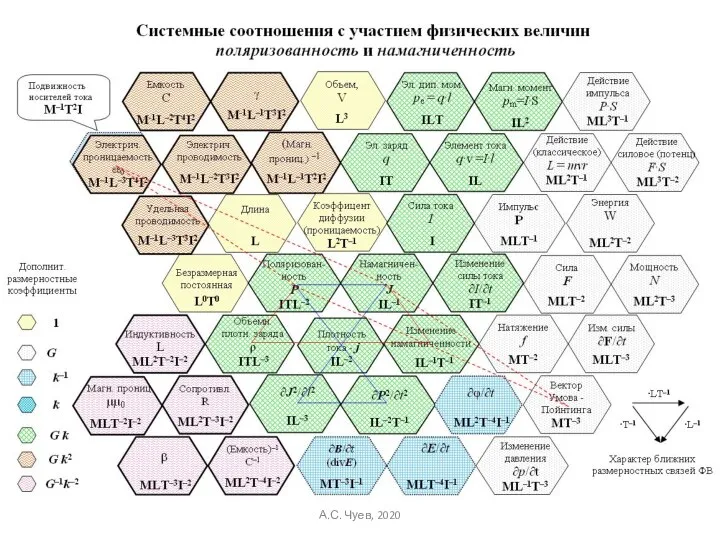
- 49. Выражение полевых электромагнитных величин через «материальные» А.С. Чуев, 2020
- 50. А.С. Чуев, 2020
- 51. А.С. Чуев, 2020
- 52. А.С. Чуев, 2020
- 53. А.С. Чуев, 2020
- 54. А.С. Чуев, 2020
- 56. Скачать презентацию





































 Многоповерхностная теория пластичности с одной активной поверхностью
Многоповерхностная теория пластичности с одной активной поверхностью Постоянный электрический ток. Сила тока. Электродвижущая сила
Постоянный электрический ток. Сила тока. Электродвижущая сила Основы термодинамики. Внутренняя энергия
Основы термодинамики. Внутренняя энергия Презентация на тему Применение законов Ньютона
Презентация на тему Применение законов Ньютона  Явление фотоэффекта. Внешний фотоэффект
Явление фотоэффекта. Внешний фотоэффект Tesla
Tesla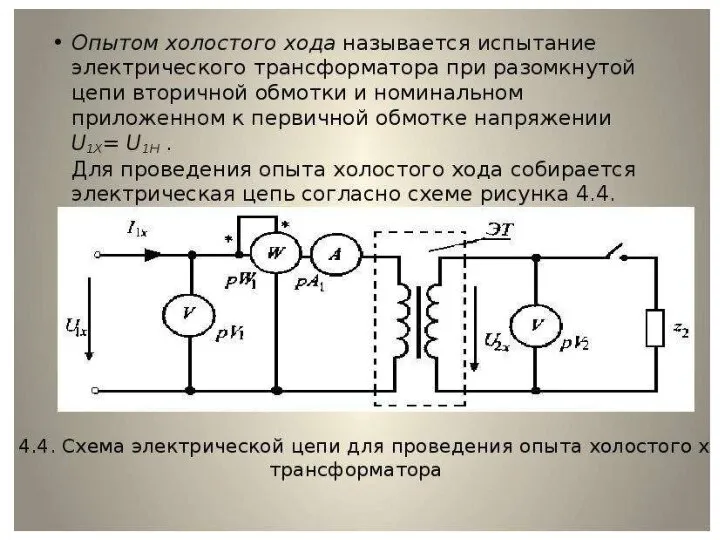 Опыт холостого хода
Опыт холостого хода Уплотняющие и опорные органы сельскохозяйственных машин
Уплотняющие и опорные органы сельскохозяйственных машин Презентация на тему Тепловые машины и их КПД
Презентация на тему Тепловые машины и их КПД  Беттік жетекті винттік сорғыш қондырғының штанг бағаналарында болатын тербеліс механизмін зерттеу
Беттік жетекті винттік сорғыш қондырғының штанг бағаналарында болатын тербеліс механизмін зерттеу Кристаллические и аморфные тела
Кристаллические и аморфные тела Состав и строение атома
Состав и строение атома Технологии обработки металлов, выполняемые в ССХТ
Технологии обработки металлов, выполняемые в ССХТ Электрический ток в жидкостях
Электрический ток в жидкостях Изменения агрегатных состояний вещества. Физический диктант
Изменения агрегатных состояний вещества. Физический диктант Электричество. Электрический ток
Электричество. Электрический ток Электризация тел
Электризация тел Презентация на тему Температура
Презентация на тему Температура  Электрический ток в жидкостях. Электролиз
Электрический ток в жидкостях. Электролиз Радіолокація. Радіомовлення і телебачення. Супутникове телебачення. 11 клас
Радіолокація. Радіомовлення і телебачення. Супутникове телебачення. 11 клас Выбор проводников по термической стойкости
Выбор проводников по термической стойкости Энергосбережение. Исследовательская работа
Энергосбережение. Исследовательская работа Закон Ома. Светодиоды. Кнопки
Закон Ома. Светодиоды. Кнопки Презентация на тему Атмосфера Земли. Атмосферное давление
Презентация на тему Атмосфера Земли. Атмосферное давление  21 061
21 061 Тема урока: Электрическое сопротивление Открываем новое свойство тел!
Тема урока: Электрическое сопротивление Открываем новое свойство тел! _DyjvLh93NEyw_UEOvluXQ
_DyjvLh93NEyw_UEOvluXQ Фазовые и структурные превращения в оболочках ТВЭЛов из сплава Э110 в условиях сухого хранения
Фазовые и структурные превращения в оболочках ТВЭЛов из сплава Э110 в условиях сухого хранения