Содержание
- 2. Квантовая статистика –раздел физики, исследующий поведение многих частиц, подчиняющихся квантовым законам.
- 3. ПРИНЦИП НЕРАЗЛИЧИМОСТИ ТОЖДЕСТВЕННЫХ ЧАСТИЦ Будем рассматривать многоэлектронные системы Если частицы имеют одинаковые физические характеристики ( масса,
- 4. В классической механике можно всегда отследить поведение частицы – ее траектория известна
- 5. В квантовой механике понятия траектории нет Можно говорить только о вероятности обнаружения частицы в данной точке
- 6. Если волновые функции двух частиц перекрываются, то решить вопрос, какая из двух частиц находится в данной
- 7. ПРИНЦИП неразличимости тождественных частиц Невозможно экспериментально различить тождественные частицы
- 8. Если обозначить волновую функцию системы 2 электронов Совокупность пространственных и спиновых координат i частицы Частицы поменялись
- 9. Из принципа неразличимости Симметричная волновая функция Антисимметричная волновая функция
- 10. Симметрия или антисимметрия определяется спином частиц Частицы с полуцелым спином (электроны, протоны, нейтроны) описываются антисимметричными волновыми
- 11. Поведение фермионов описывается статистикой Ферми-Дирака Поведение бозонов - статистикой Бозе -Эйнштейна
- 12. Обобщенный принцип Паули Системы фермионов встречаются в природе только в состояниях, описываемых антисимметричными волновыми функциями. Количество
- 13. РАСПРЕДЕЛЕНИЕ ФЕРМИ-ДИРАКА Вероятность обнаружения электрона с энергией Е при температуре Т - Уровень Ферми (химический потенциал)
- 14. При Т=0
- 15. При Т=0
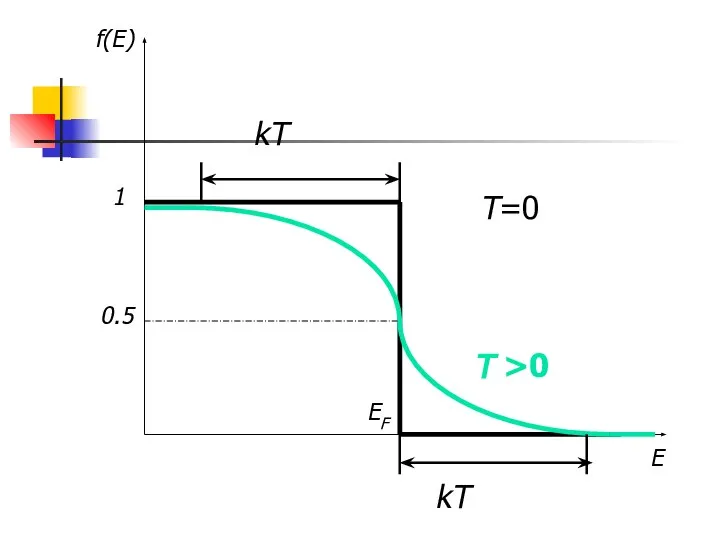
- 16. Е f(Е) 1 ЕF Т=0 0.5 Т >0 kT kT
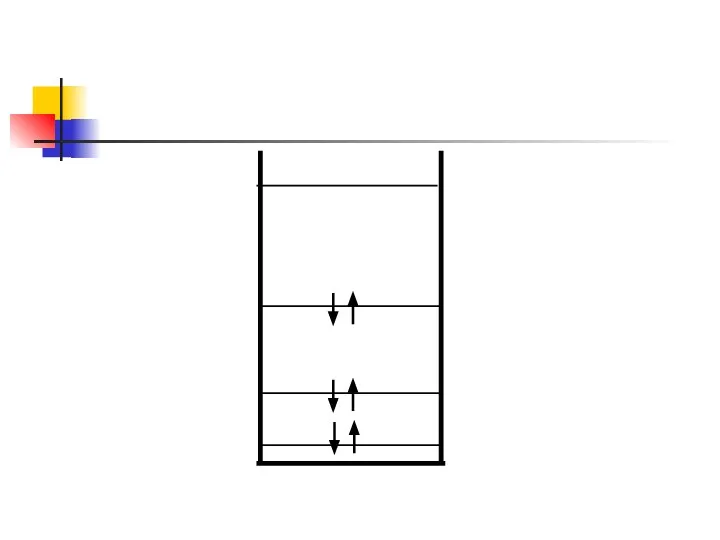
- 18. 1) Электроны заполняют нижние уровни в соответствие с принципом Паули 2) При Т=0 максимально возможная энергия
- 19. Электронный газ называется вырожденным и подчиняется статистике Ферми-Дирака Электронный газ называется невырожденным и подчиняется статистике Больцмана
- 20. Статистика Бозе-Эйнштейна EB – химический потенциал системы бозонов
- 21. ФИЗИКА ТВЕРДОГО ТЕЛА
- 22. Металлы,диэлектрики, полупроводники В твердом теле при сближении атомов отдельные уровни расщепляются и объединяются в зоны
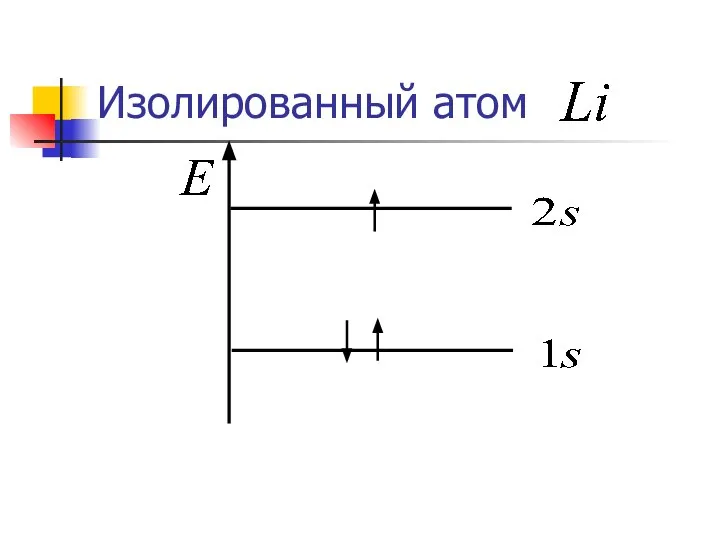
- 24. Изолированный атом
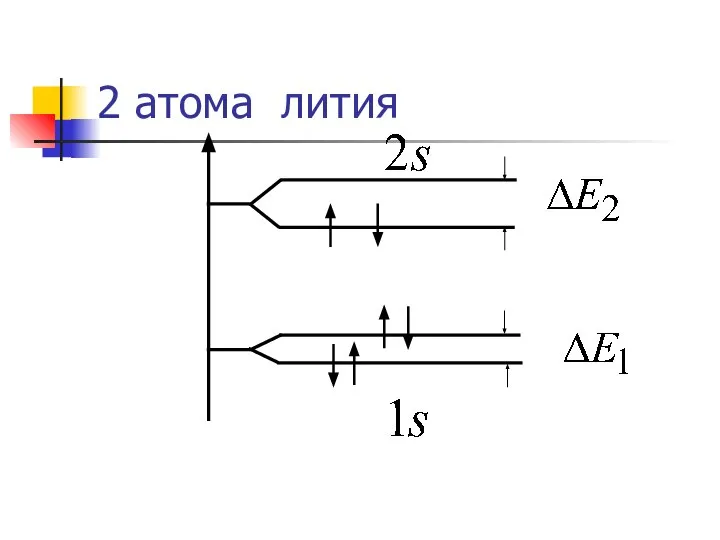
- 25. 2 атома лития
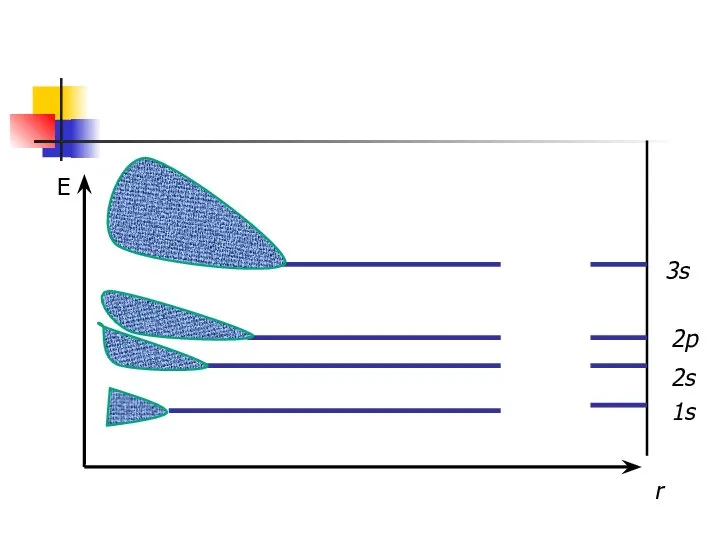
- 26. Е r 1s 2s 2p 3s
- 27. Образуются разрешенные области энергии В разрешенной зоне столько дискретных уровней ,сколько их содержится во всех изолированных
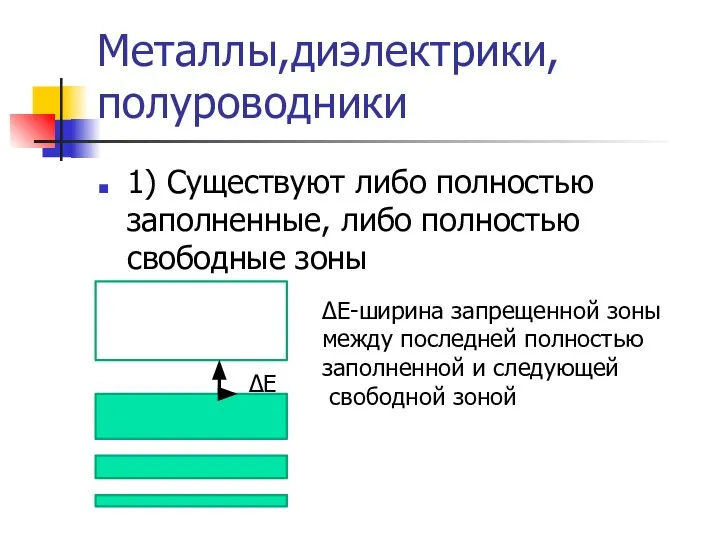
- 28. Металлы,диэлектрики, полуроводники 1) Существуют либо полностью заполненные, либо полностью свободные зоны ∆E ∆E-ширина запрещенной зоны между
- 29. Если ∆E Электрону может хватить тепловой энергии, чтобы перейти из одной зоны в другую Если ∆E
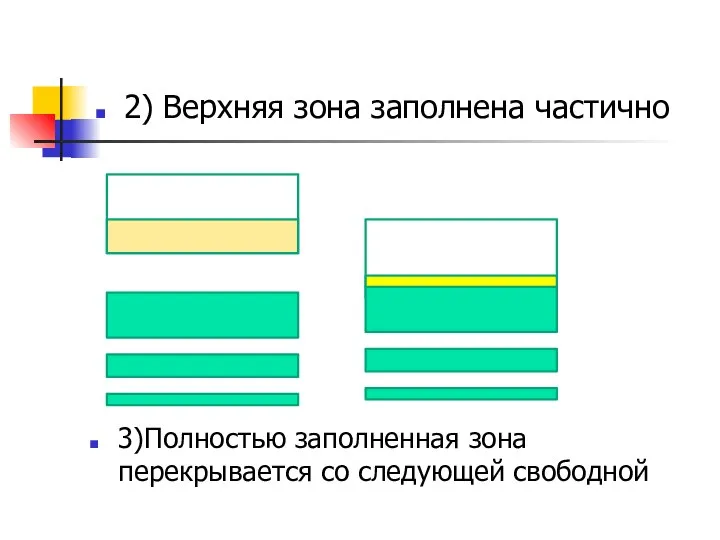
- 30. 2) Верхняя зона заполнена частично 3)Полностью заполненная зона перекрывается со следующей свободной
- 31. Такие вещества называются металлами
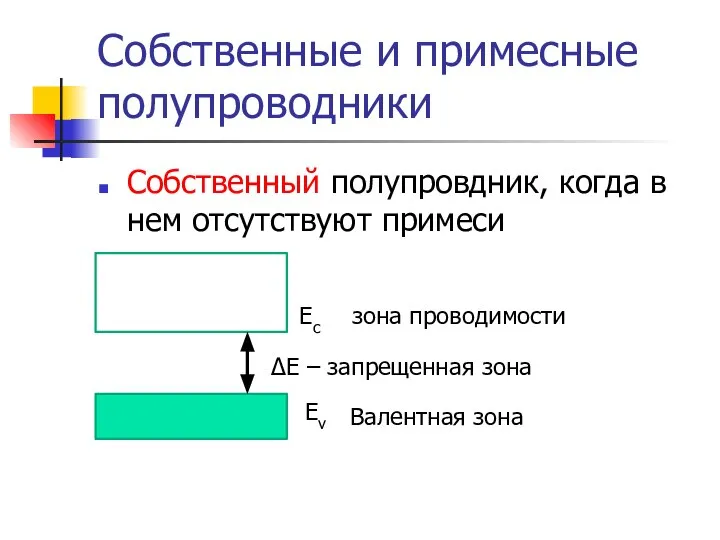
- 32. Собственные и примесные полупроводники Собственный полупровдник, когда в нем отсутствуют примеси Eс Валентная зона Ev зона
- 33. Примесный полупроводники – в кристаллической решетки встречаются атомы посторонней примеси
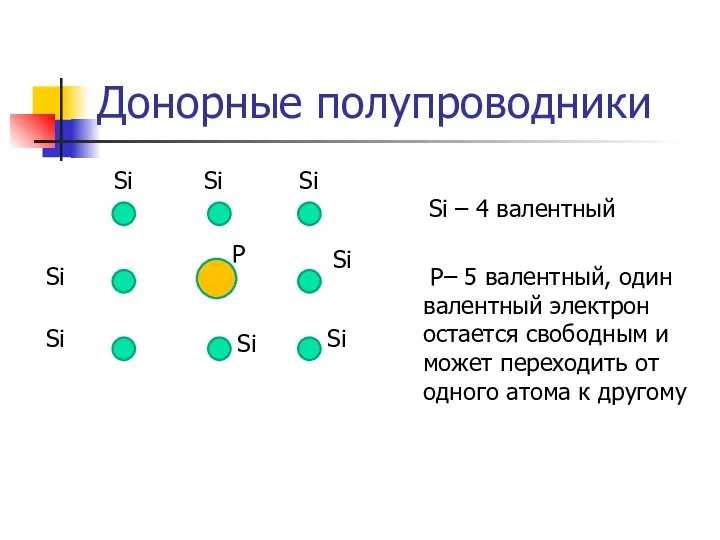
- 34. Донорные полупроводники Si Si Si Si Si Si Si Si P Si – 4 валентный P–
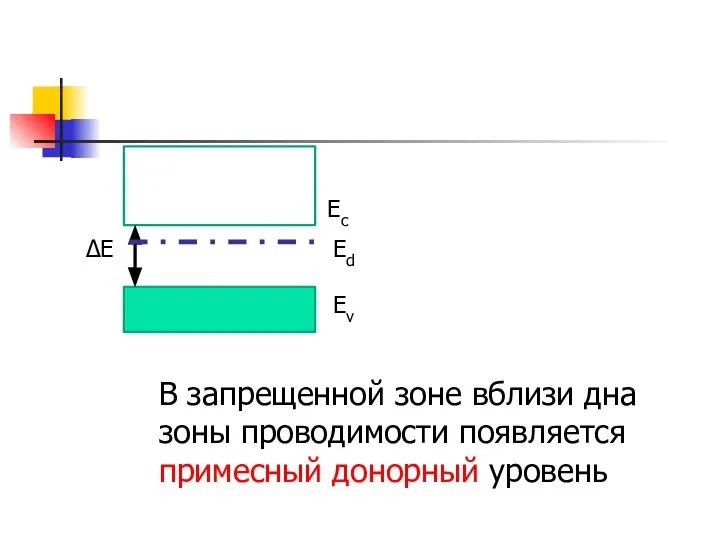
- 35. Eс Ev ∆Е Ed В запрещенной зоне вблизи дна зоны проводимости появляется примесный донорный уровень
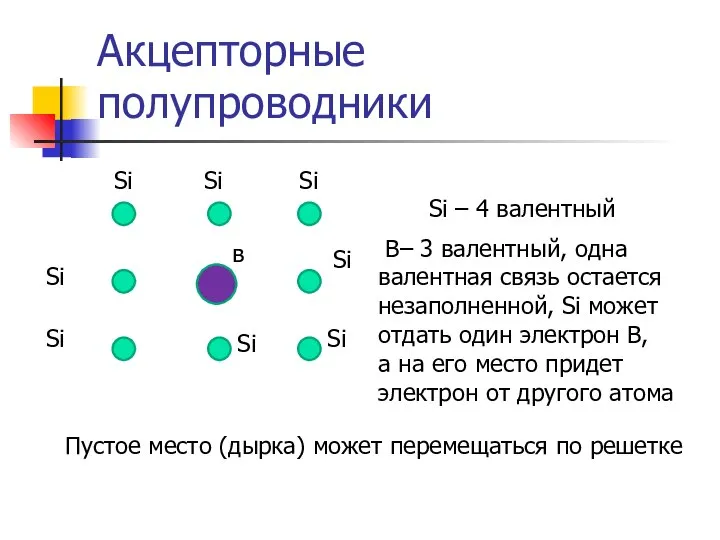
- 36. Акцепторные полупроводники Si Si Si Si Si Si Si Si в Si – 4 валентный В–
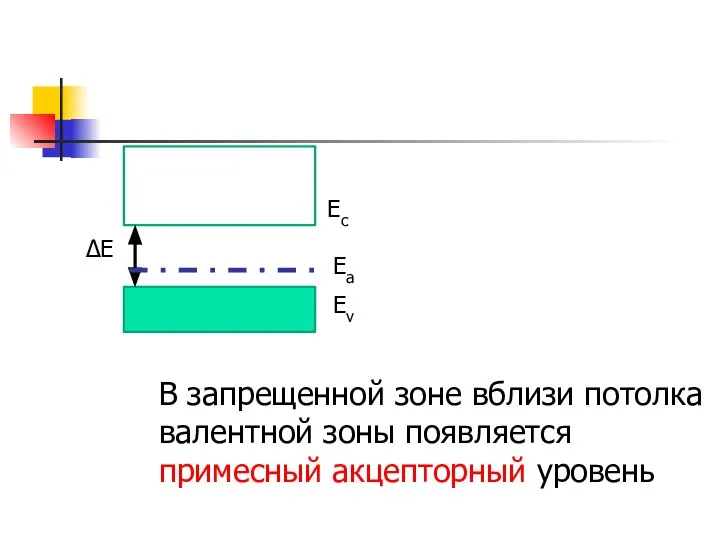
- 37. Ec Ev ∆Е Eа В запрещенной зоне вблизи потолка валентной зоны появляется примесный акцепторный уровень
- 38. Движение электрона в кристалле В кристалле на электрон действует поле кристаллической решетки Поведение электронов в кристалле
- 39. Эффективная масса электрона Эффективная масса учитывает взаимодействие электрона с кристаллической решеткой и позволяет описывать его движение
- 41. Скачать презентацию











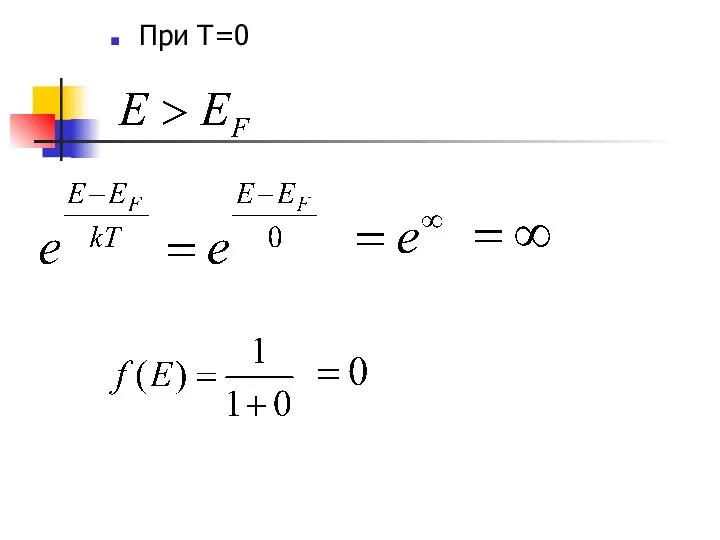
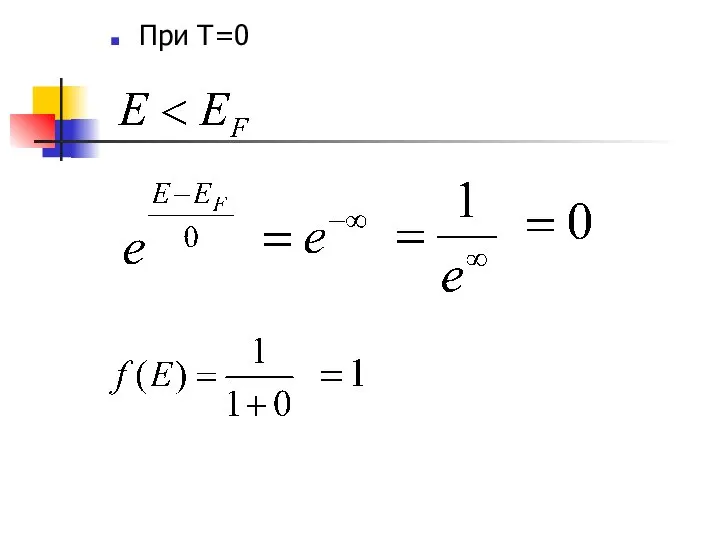
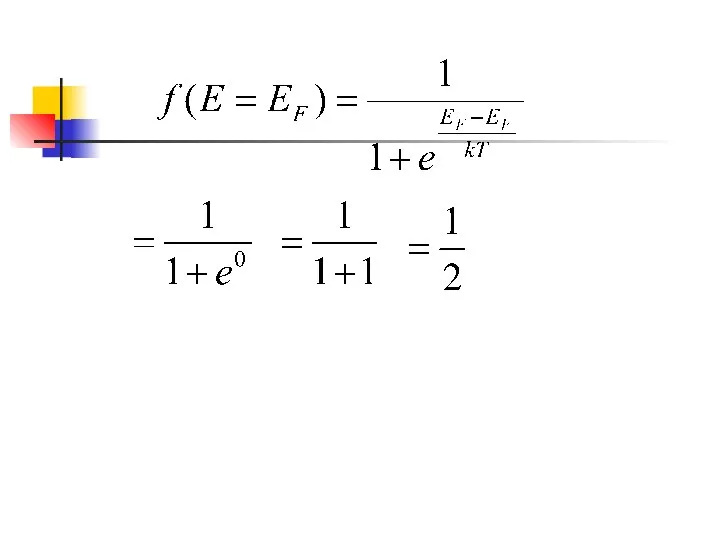











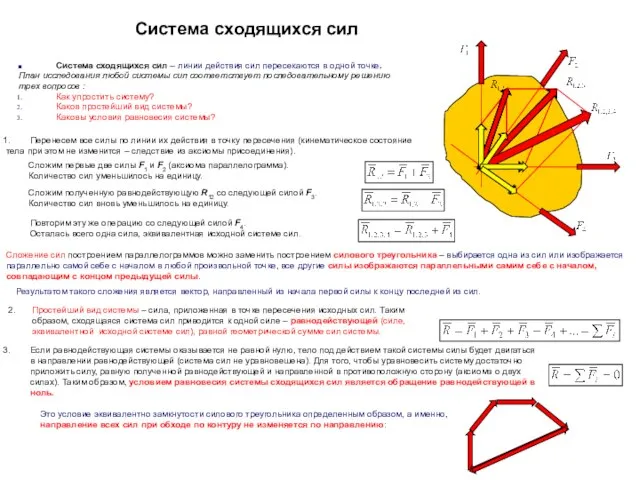 Система сходящихся сил
Система сходящихся сил Презентация на тему Электрическое поле (10 класс)
Презентация на тему Электрическое поле (10 класс)  Система охлаждения двигателя
Система охлаждения двигателя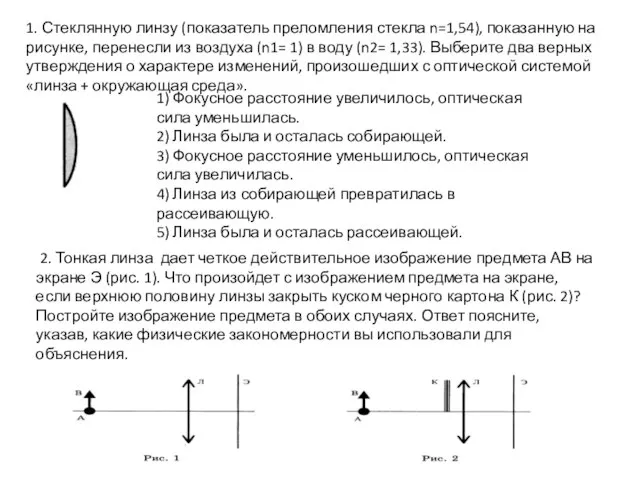 Линза. Фокусное расстояние
Линза. Фокусное расстояние Равновесие сил с учётом трения покоя, сцепления
Равновесие сил с учётом трения покоя, сцепления Молекулярная физика. Тепловые явления
Молекулярная физика. Тепловые явления Отражение света
Отражение света Пара сил и момент силы относительно точки
Пара сил и момент силы относительно точки Технология и организация судоремонта
Технология и организация судоремонта Навигация по геофизическим полям
Навигация по геофизическим полям Проект: Кошкина радость
Проект: Кошкина радость Диффузия в газах, жидкостях и твердых телах
Диффузия в газах, жидкостях и твердых телах Случайности не случайны! А вас бьет током? 4 класс
Случайности не случайны! А вас бьет током? 4 класс Общая фармакопейная статья
Общая фармакопейная статья Инфразвук и ультразвук
Инфразвук и ультразвук Конденсаторы. Ёмкость плоского конденсатора. Энергия электрического поля конденсатора
Конденсаторы. Ёмкость плоского конденсатора. Энергия электрического поля конденсатора Материаловедение и технологии конструкционных материалов
Материаловедение и технологии конструкционных материалов Коэффициент теплоотдачи при кипении
Коэффициент теплоотдачи при кипении Понятие о машинах и механизмах
Понятие о машинах и механизмах Svobodnoe_padenie_tel_Dvizhenie_s_uskoreniem_svobodnogo_padenia
Svobodnoe_padenie_tel_Dvizhenie_s_uskoreniem_svobodnogo_padenia Модель атома Томсона
Модель атома Томсона Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения. Развитие ядерной энергетики
Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения. Развитие ядерной энергетики Прижимы: схемы и расчет
Прижимы: схемы и расчет Презентация на тему Перемещение при прямолинейном равноускоренном движении (9 класс)
Презентация на тему Перемещение при прямолинейном равноускоренном движении (9 класс)  Склокомпозиційні матеріали для спаювання з широким інтервалом ТКЛР
Склокомпозиційні матеріали для спаювання з широким інтервалом ТКЛР Презентация на тему Движение тел по наклонной плоскости
Презентация на тему Движение тел по наклонной плоскости  Манипулятор. Занятие 3
Манипулятор. Занятие 3 Физические величины. Измерение физических величин. Точность и погрешность измерений
Физические величины. Измерение физических величин. Точность и погрешность измерений