Геометрия червячного колеса. Лекция 17

3.3. Геометрия червячного колеса.
а) Без смещения
- делительный диаметр;
и -
диаметры вершин и впадин;
- ширина зубчатого венца;
- наиболь-
ший диаметр червячного колеса;
- межосевое расстояние
б) Со смещением
В ЧП часто используется смещение,
чтобы вписаться в округленное или стандарт. межосевое расстояние. Причина в том, что имеет только 3 значения и много ГОСТир. параметров ( , ).
При смещении: - у червяка меняется только
Вводится угол подъема витков резьбы по
- у червячного колеса на « » меняются все диаметры, кроме
Межосевое расстояние . Для выбора имеем
следующую систему: - ; - ; - и имеют
значения по ГОСТ; - условие контактной выносливости выполняется;
- условие изгибной выносливости выполняется. !!! Всё это одновременно
2

3.4. Кинематика ЧП. Низкий КПД ЧП объясняется особенностями кинематики
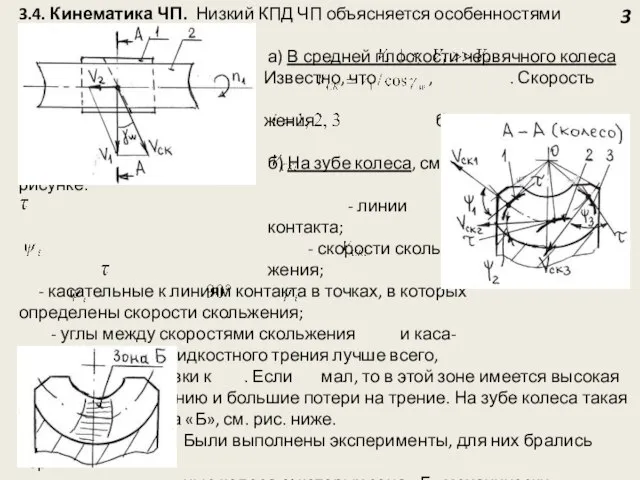
а) В средней плоскости червячного колеса
Известно, что , . Скорость сколь-
жения большая по величине = (–)
б) На зубе колеса, см. А – А на левом рисунке.
- линии
контакта;
- скорости сколь-
жения;
- касательные к линиям контакта в точках, в которых
определены скорости скольжения;
- углы между скоростями скольжения и каса-
тельными . Для жидкостного трения лучше всего,
чтобы были близки к . Если мал, то в этой зоне имеется высокая склонность к заеданию и большие потери на трение. На зубе колеса такая зона есть – это зона «Б», см. рис. ниже.
Были выполнены эксперименты, для них брались червяч-
ные колеса, у которых зона «Б» механически удалялась.
КПД такой ЧП значительно увеличивался, что является
доказательством наших предположений, но прочность
зуба на изгиб существенно снижалась. Поэтому такие
ЧП не применяются.
3

3.5. Материалы деталей ЧП.
Из-за высокой необходимо использовать антифрикционные пары, в кото-рых один материал жесткий и твердый – СТАЛЬ, а другой – мягкий.
В машиностроении червяк, являющийся конструктивно нежестким, изготавли-вают из стали: - малоуглеродистой (15Х, 20Х, 18 ХГТ, … ) с ТО цементация;
- среднеуглеродистой (40Х, 40ХН, 35ХМ, … ) с ТО улучшение + закалка ТВЧ.
Архимедовы червяки изготавливают из среднеуглеродистой стали с ТО улучшен.
Требования, предъявляемые к червяку: высокие прочность, жесткость и твердость; малая шероховатость (витки шлифуют и полируют); низкая склон-ность к заеданию.
Червячные колеса изготавливают из материалов, которые условно можно разделить на 3 группы.
I группа – оловянные бронзы (БрО10Ф1, БрО5Ц5С6, …).
Их применяют, если . Эти материалы дорогие,
поэтому колесо изготавливают сборным (венец из бронзы,
а ступица – из чугуна, редко из стали).
II группа – безоловянные бронзы (БрА9Ж3Л и др.) и латуни
(ЛАЖМц66-6-3-2 и др.). Их применяют, если
Они дешевле предыдущих материалов, но червячные колеса
также изготавливают сборными.
III группа – чугуны (СЧ15, СЧ20, …). Применяют, если . Чугун деше-вый материал, поэтому колеса целиком изготавливают из одного материала.
4

3.6. Причины выхода из строя ЧП. В работающей ЧП возникают и .
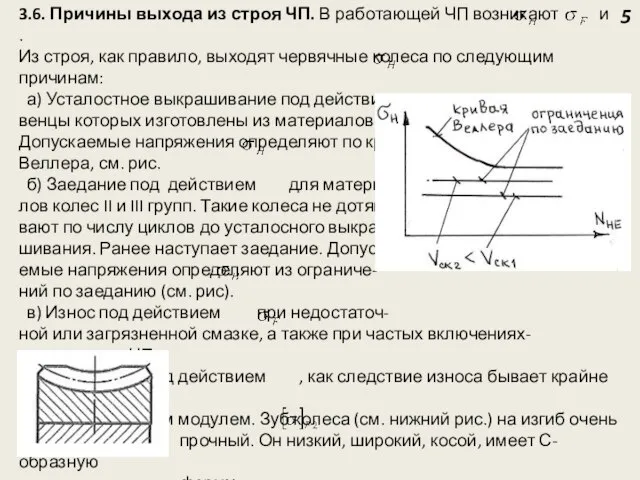
Из строя, как правило, выходят червячные колеса по следующим причинам:
а) Усталостное выкрашивание под действием характерно для колес, венцы которых изготовлены из материалов I группы, а смазка чистая. Допускаемые напряжения определяют по кривым усталости
Веллера, см. рис.
б) Заедание под действием для материа-
лов колес II и III групп. Такие колеса не дотяги-
вают по числу циклов до усталосного выкра-
шивания. Ранее наступает заедание. Допуска-
емые напряжения определяют из ограниче-
ний по заеданию (см. рис).
в) Износ под действием при недостаточ-
ной или загрязненной смазке, а также при частых включениях-отключениях ЧП.
г) Излом зуба под действием , как следствие износа бывает крайне редко
для колес с малым модулем. Зуб колеса (см. нижний рис.) на изгиб очень
прочный. Он низкий, широкий, косой, имеет С-образную
форму.
Для расчета на изгибную выносливость допускаемые
напряжения определяют по кривым усталости
Веллера.
5

3.7. Особенности расчета ЧП.
Для расчета используют условия контактной и изгибной выносливости. Пос-
леднее в виде проверочного расчета.
Расчет проводят методом последовательных приближений (итераций), т.к. все основные параметры ЧП (даже выбор материала колеса) зависят от , а ее можно точно определить только в конце расчета по известным геометри-ческим параметрам.
Для 1-го приближения используют следующие эмпирические зависимости
; символ «’» говорит о приближении.
По выбирают материал колеса. Далее определяют геометрические па-раметры и для них величину . Затем проверяют условия контактной и изгибной выносливости, рассчитанные по точным зависимостям.
Если хотя бы одно условие не выполняется, то переходят ко 2-му прибли-жению, для которого берут таким, какое получилось в конце 1-го при-ближения.
И так далее, пока оба условия не выполнятся.
6

3.8. Расчетная нагрузка больше номинальной в раз, где
- коэффициент нагрузки.
3.8.1. Коэффициент концентрации нагрузки на зубе колеса из-за деформа-ций нежесткого червяка. Из-за прогиба вала-червяка колесо контактирует как бы с червяком большего диаметра (см. рис. внизу). Отсюда их углы не сов-падают и происходит концентрация нагрузки (см. рис. справа)
а) До начала приработки.
где - коэф. деформации червяка
(х-ка его жесткости );
б) После приработки.
,
где - коэффициент режима
3.8.2. Коэффициент внутренней динамической нагрузки .
ЧП косозубая, колесо мягкое, отсюда хорошая приработка и плавная и бесшум-
ная работа. Поэтому при , а для ЧП очень
большая скорость.
7

3.9. КПД червячного редуктора.
Поэтому основные потери в червячном редукторе составляют потери в ЧП.
Эти потери велики, так как червяк – это винт, а для него ,
где: - угол подъема витка по ;
- приведенный угол трения.
Для повышения КПД ЧП надо:
- повысить за счет: - увеличения , но по ГОСТ РФ , см. график;
- уменьшить , но
- уменьшить за счет: - снижения коэф.
трения (качественные антифрикционные
материалы, качественная смазка, сниже-)
ние шероховатости червяка, повышение
его твердости и т.д.);
- совершенствования
геометрии в зоне зацепления и т.д.
8

3.10. Силы в зацеплении.
Дано:
Допущения:
По 3-му закону Ньютона,
см. схему, имеем:
Из уравнения равнове-
сия червячного колеса
Из уравнения равновесия червяка
Из геометрии (см. сечение А – А)
9