Колебания. Лекция № 1

Литература
Т. И. Трофимова. Курс физики
§§140 – 148;
А. А. Детлаф, Б. М. Яворский.
Курс физики гл. 27, 28.
Н. П. Калашников,
Н. М. Кожевников,
4 ДЕ, задания 17 – 20.

- процессы, повторяющиеся во времени, их тип определяет природа процесса.
Различают колебания: механические,
электромагнитные, электромеханические и другие.
Колебания

Периодические - повторяются через равные промежутки времени.
Гармонические - описываются законом синуса или косинуса.
Колебания

Механические колебания
Опыт Кавендиша

Механические колебания
При абсолютно упругом ударе шаров (нет потерь энергии) скорость и угол отклонения крайних шаров одинаковы, промежуточные шары - в покое.

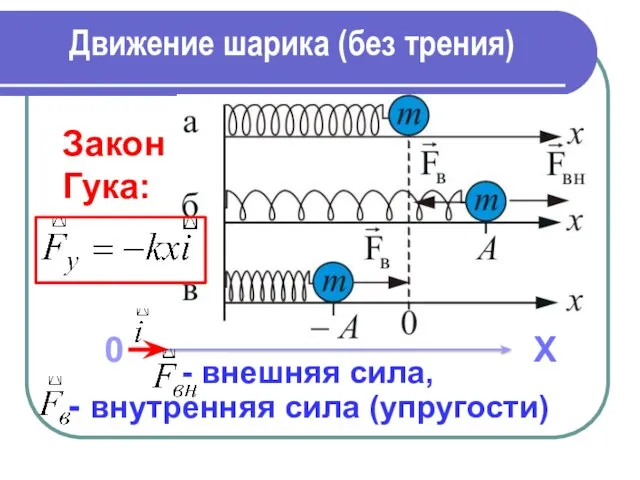
Движение шарика (без трения)
Х
0
- внешняя сила,
- внутренняя сила (упругости)
Закон
Гука:

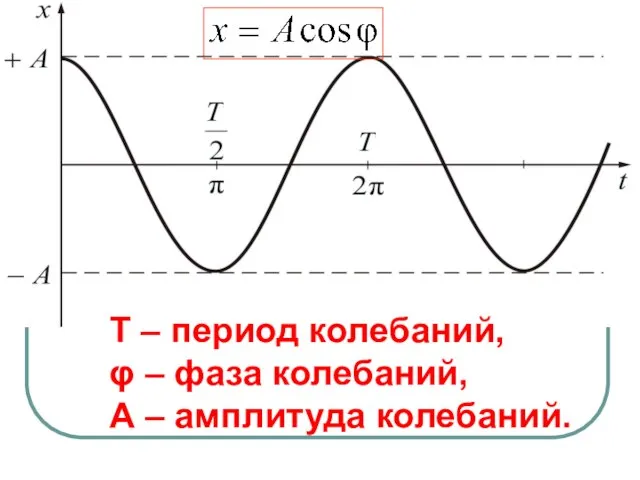
0
М Т
X
Механические колебания
- координата (смещение) МТ
в момент времени t;
- максимальное смещение (амплитуда колебаний);

0
М Т
X
Механические колебания
0
- циклическая частота;
- начальная фаза колебаний;
- фаза колебаний;

Т – период колебаний,
φ – фаза колебаний,
А – амплитуда колебаний.

Скорость и ускорение
скорость МТ, совершающей ГК;
ускорение МТ.

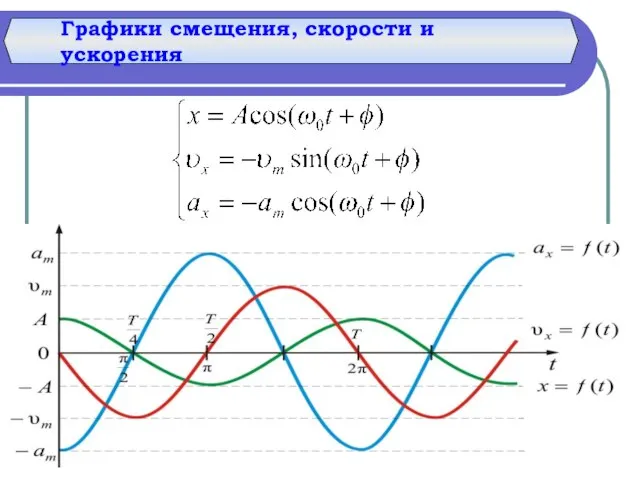
Графики смещения, скорости и ускорения

cкорость колебаний максимальна и равна амплитуде скорости в момент прохождения через положение равновесия;
при максимальном смещении скорость равна нулю;
ускорение равно нулю при прохождении телом положения равновесия и достигает наибольшего значения, равного амплитуде ускорения при наибольших смещениях.
Из графиков следует:

Уравнение динамики гармонических
колебаний
Второй закон Ньютона в проекции на ось ОХ:
Сила пропорциональна смещению и всегда направлена к положению равновесия. Период и фаза силы совпадают с периодом и фазой ускорения.
Этому условию удовлетворяют упругие силы. Силы иной природы, удовлетворяющие этому условию - квазиупругие.
Для квазиупругой силы
где k – коэффициент квазиупругой силы.

получим уравнение динамики ГК, вызываемых упругими силами:
Его решение или
- уравнение динамики гармонических колебаний.
Учитывая, что и ,

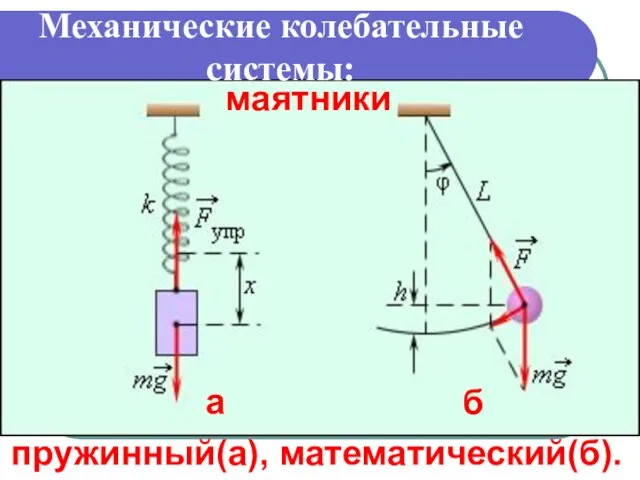
Механические колебательные
cистемы:
a
б
пружинный(а), математический(б).
маятники

Гармонические осцилляторы
1. Пружинный маятник – груз массой m, подвешен-ный на абсолютно упругой пружине с жесткостью k, совершающий гармони-ческие колебания под действием упругой силы.
Циклическая частота и период собственных
колебаний

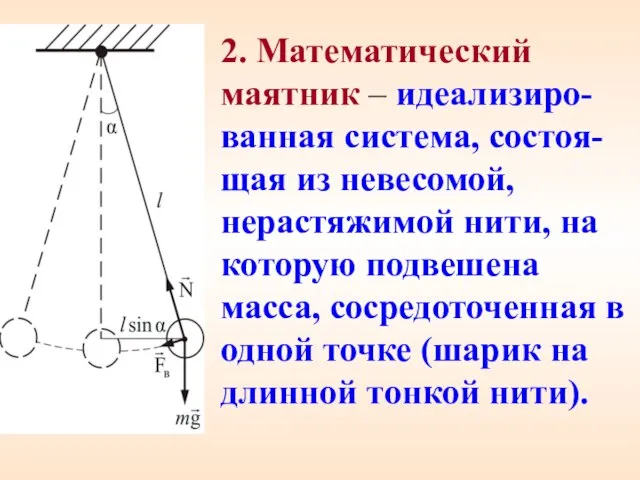
2. Математический маятник – идеализиро-ванная система, состоя-щая из невесомой, нерастяжимой нити, на которую подвешена масса, сосредоточенная в одной точке (шарик на длинной тонкой нити).

Уравнение динамики вращательного движения
При отклонении маятника от вертикали, возникает вращающий момент Момент инерции маятника
Угловое ускорение
Обозначим
Для малых углов

Тогда
, или
его решение
Уравнение движения маятника
Циклическая частота и период собствен-ных колебаний математического маятника

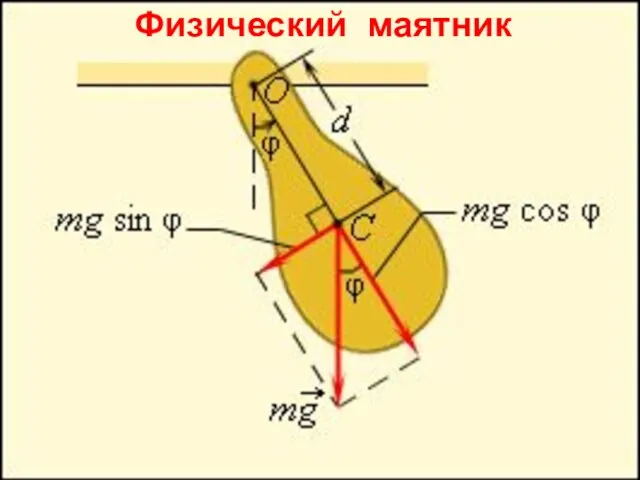
Физический маятник

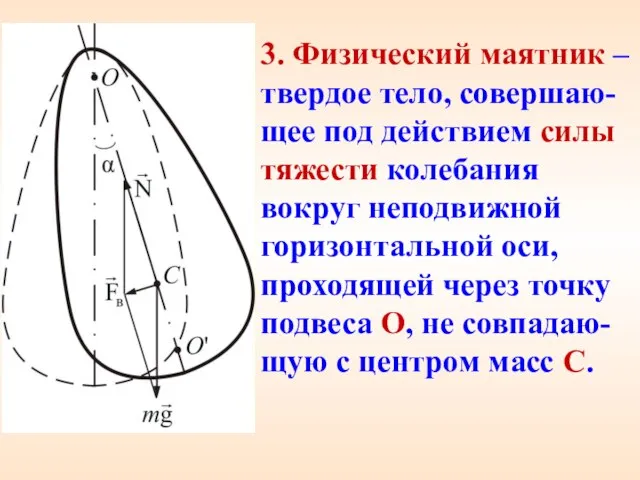
3. Физический маятник – твердое тело, совершаю-щее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку подвеса О, не совпадаю-щую с центром масс С.

Вращающий момент силы тяжести
Уравнение динамики вращательного движения его решение
– расстояние между точкой подвеса и центром инерции маятника О-С,
J – момент инерции маятника относитель-но точки подвеса O.

–длина математического маятника,
период колебания которого совпадает с периодом колебаний данного физического маятника.
Циклическая частота и период собствен-
ных колебаний физического маятника
Обозначим - приведенная длина
физического маятника, тогда

Соотношения для математического и физического маятников справедливы для малых углов отклонения (меньше 15°), когда мало отличается от длины хорды (меньше, чем на 1%).

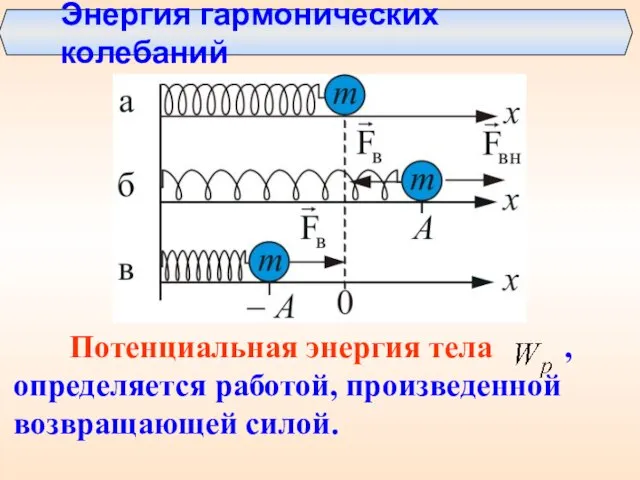
Энергия гармонических колебаний
Потенциальная энергия тела , определяется работой, произведенной возвращающей силой.

Кинетическая энергия:
Полная энергия:
Потенциальная энергия:
Полная механическая энергия тела,
совершающего ГК, пропорциональна
квадрату амплитуды.

При ГК, совершающихся под действием консервативных сил, происходит переход кинетической энергии в потенциальную и обратно, но их сумма в любой момент времени постоянна.

Это электрическая цепь, состоя-щая из конденсатора емкостью С и катушки индуктивностью L.
В нем возникают электромагнит-ные колебания: изменяются по гармоническому закону
Колебательный контур

Закон Ома для участка 1-R-L-2:
Свободные колебания

Незатухающие свободные колебания

Затухающие колебания

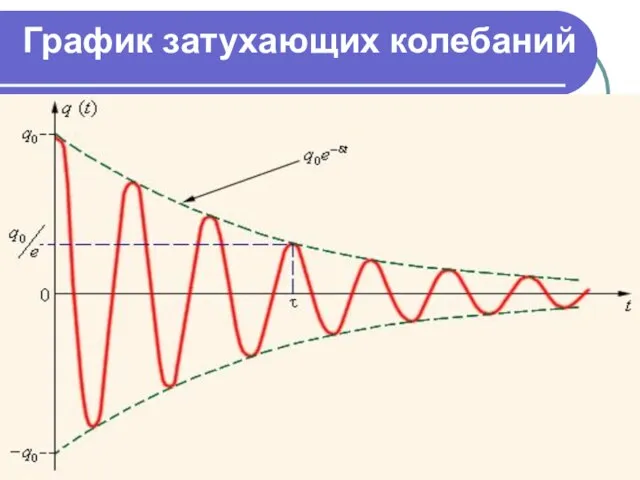
График затухающих колебаний

0
График затухающих колебаний
- коэффициент затухания;
- амплитуда затуха-ющих колебаний;
логарифмический
декремент
затухания;

Для получения незатухающих колебаний в контур включают источник переменной ЭДС.
Вынужденные колебания

решение неоднородного уравнения,
- амплитуда,
установившихся вынужденных колебаний.
- начальная фаза
где