из некоторого определенного (начального) положения.
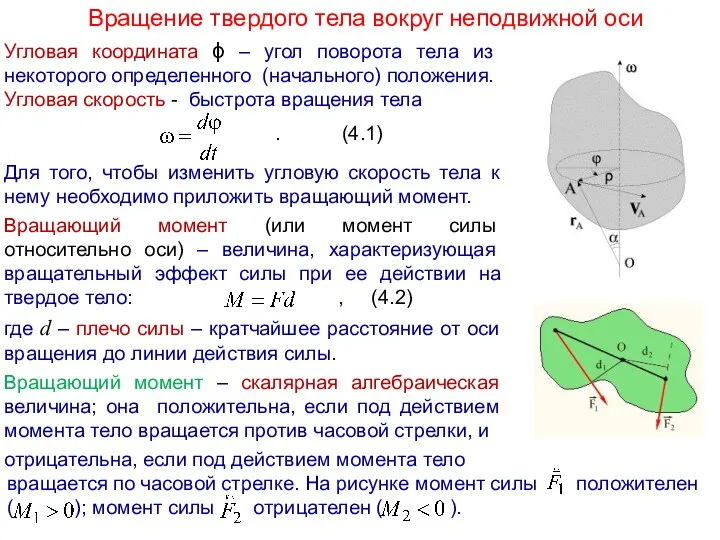
Угловая скорость - быстрота вращения тела
. (4.1)
Для того, чтобы изменить угловую скорость тела к нему необходимо приложить вращающий момент.
Вращающий момент (или момент силы относительно оси) – величина, характеризующая вращательный эффект силы при ее действии на твердое тело: , (4.2)
где d – плечо силы – кратчайшее расстояние от оси вращения до линии действия силы.
Вращающий момент – скалярная алгебраическая величина; она положительна, если под действием момента тело вращается против часовой стрелки, и
отрицательна, если под действием момента тело
вращается по часовой стрелке. На рисунке момент силы положителен
( ); момент силы отрицателен ( ).
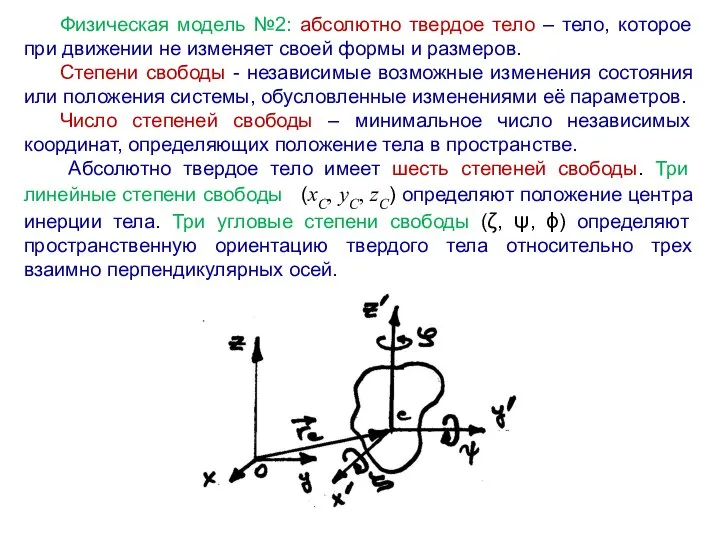
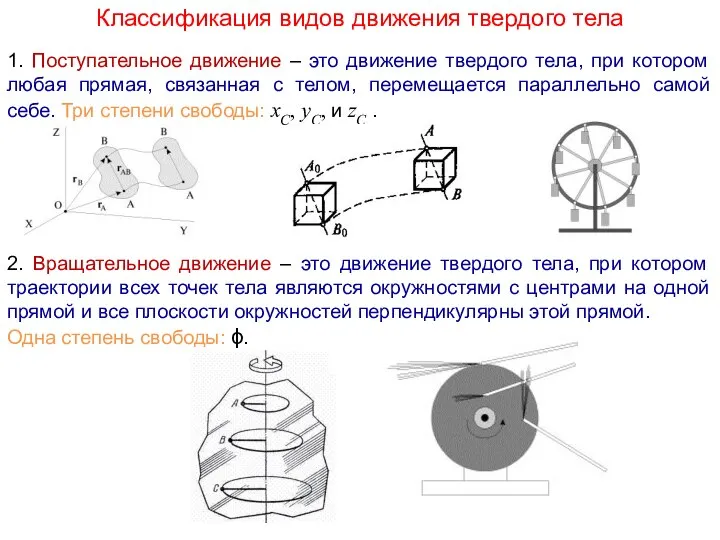
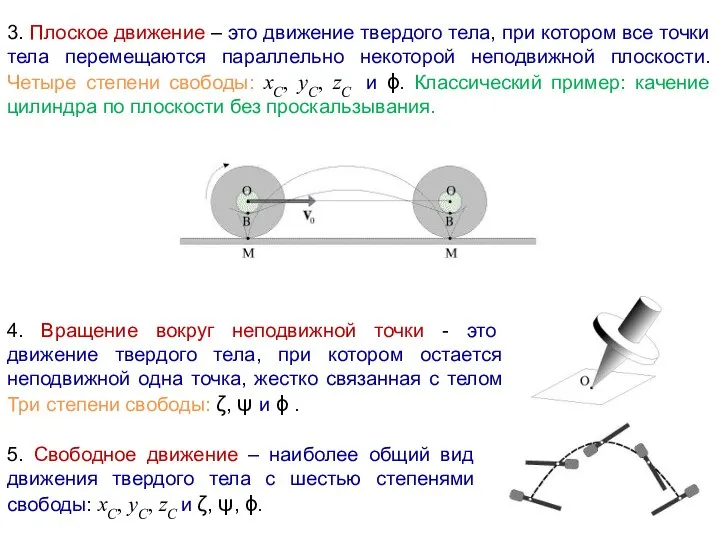


 Оптические МЭМС. Актуаторы для оптических МЭМС-микрозеркала. Технология DLP
Оптические МЭМС. Актуаторы для оптических МЭМС-микрозеркала. Технология DLP Умные полимерные гели с высокими механическими свойствами для применения в нефтедобыче
Умные полимерные гели с высокими механическими свойствами для применения в нефтедобыче Электрический ток. Лекция 24(6)
Электрический ток. Лекция 24(6) Сверхпроводимость. Эффект Мейсснера
Сверхпроводимость. Эффект Мейсснера Открытие явления электромагнитной индукции
Открытие явления электромагнитной индукции Помпаж. Способы повышения запасов ГДЛУ (борьба с помпажом)
Помпаж. Способы повышения запасов ГДЛУ (борьба с помпажом) Определение коэффициента силы трения
Определение коэффициента силы трения Электромагнетизм
Электромагнетизм Радиационный контроль дефектоскопов
Радиационный контроль дефектоскопов Строение атома
Строение атома Ионизирующее излучение
Ионизирующее излучение Качество электроэнергии. Компенсация реактивной мощности
Качество электроэнергии. Компенсация реактивной мощности Изменение внутренней энергии. Теплопередача
Изменение внутренней энергии. Теплопередача Усилитель звуковой частоты
Усилитель звуковой частоты Презентация на тему Магнитные свойства вещества (11 класс)
Презентация на тему Магнитные свойства вещества (11 класс)  Прикладная оптика. Лекция 2
Прикладная оптика. Лекция 2 Презентация на тему Трение в природе и технике
Презентация на тему Трение в природе и технике  Импульс материальной точки
Импульс материальной точки Типовые ошибки в курсовых работах. Примеры экзаменационных задач
Типовые ошибки в курсовых работах. Примеры экзаменационных задач Механическая работа
Механическая работа Диэлектриктер физикасы
Диэлектриктер физикасы Пароходы и лайнеры
Пароходы и лайнеры Второй закон Ньютона
Второй закон Ньютона Шум, вібрація. Електромагнітні поля різних частот як фактори навколишнього середовища, їх вплив на здоров’я, шляхи профілактики
Шум, вібрація. Електромагнітні поля різних частот як фактори навколишнього середовища, їх вплив на здоров’я, шляхи профілактики Электрические цели. Работа тока
Электрические цели. Работа тока Статистическая радиотехника. Импульсные случайные процессы. Лекция 4
Статистическая радиотехника. Импульсные случайные процессы. Лекция 4 Сила Ампера
Сила Ампера Последовательное соединение
Последовательное соединение