импульса, энергии и т.д. Перечисленные величины называются динамическими переменными. Так как микрочастица не является частицей в классическом понимании, то ей, строго говоря, не могут быть приписаны указанные динамические переменные.
Данное обстоятельство проявляется в том, что не для всех переменных получаются при измерениях определенные значения. Так, например, электрон имеет неопределённость координаты и проекции импульса.
Соотношение или принцип неопределенностей Гейзенберга утверждает, что невозможно одновременно точно определить значения координаты и соответствующих проекций импульса частицы:
Δх – неопределённость координаты,
Δpх – неопределённость проекции импульса,
h – постоянная Планка
Чем точнее мы знаем координаты частицы, тем менее точно мы можем определить её импульс и наоборот.
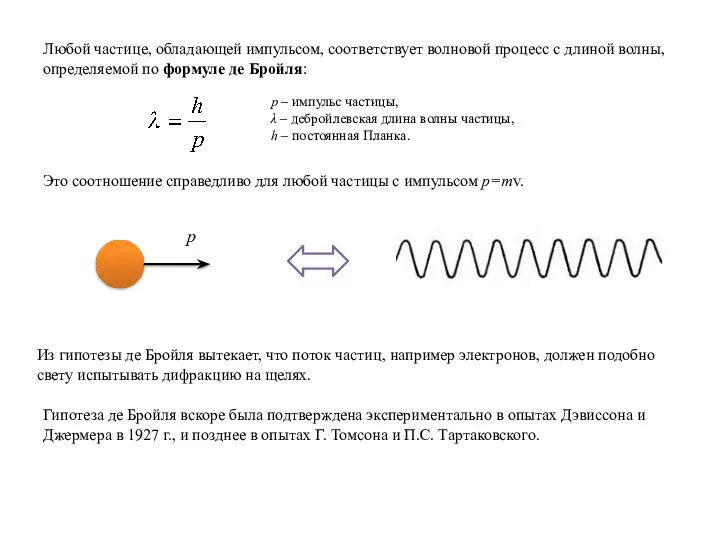
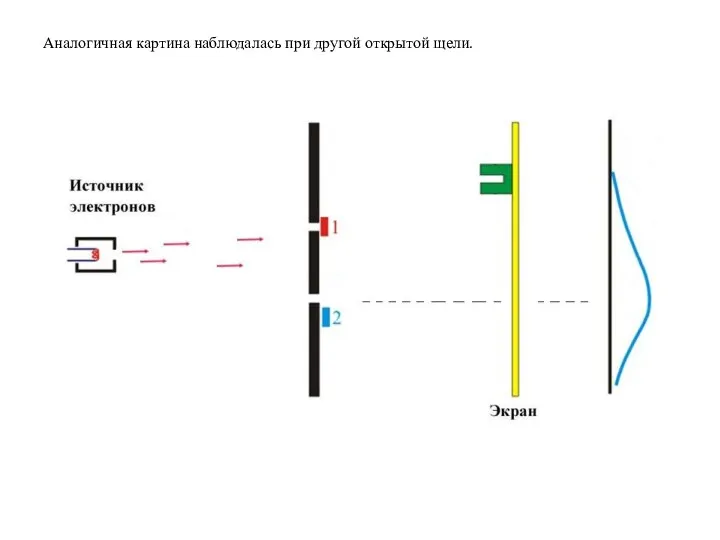
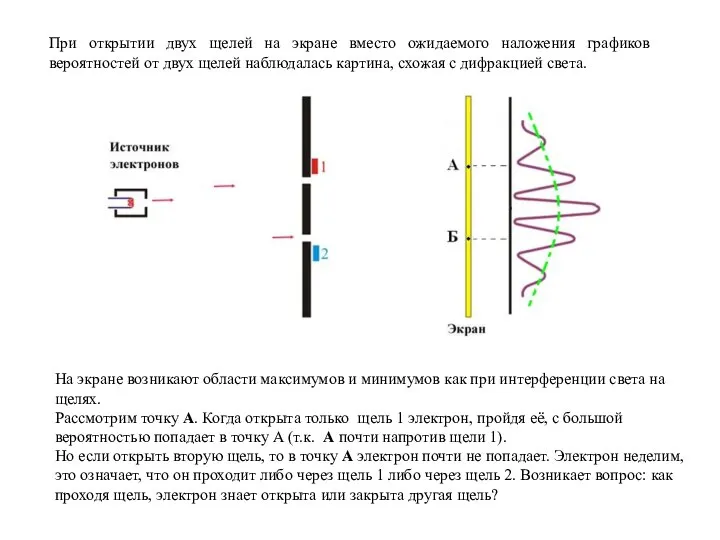
Из-за неопределённостей координаты и импульса частицы теряют смысл такое понятие как траектория. Движение микрочастицы невозможно изобразить в виде какой-нибудь линии.










 Агрегатные состояния вещества. Строение твердых, жидких и газообразных тел Урок в 7 классе Учитель физики МОУ «СОШ
Агрегатные состояния вещества. Строение твердых, жидких и газообразных тел Урок в 7 классе Учитель физики МОУ «СОШ  Анализ питьевых вод
Анализ питьевых вод Действие жидкости и газа на погружённое в них тело. Урок физики в 7 классе
Действие жидкости и газа на погружённое в них тело. Урок физики в 7 классе Сравнение количеств теплоты при смешивании воды разной температуры. Лабораторная работа № 1
Сравнение количеств теплоты при смешивании воды разной температуры. Лабораторная работа № 1 Сила упругости. Условие возникновения силы упругости - деформация
Сила упругости. Условие возникновения силы упругости - деформация Развитие средств связи
Развитие средств связи Растяжение-сжатие прямого бруса
Растяжение-сжатие прямого бруса Условие плавания тел
Условие плавания тел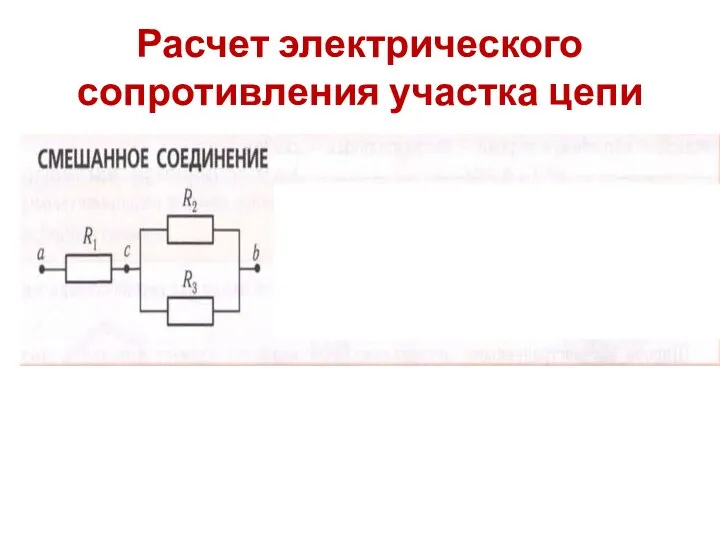 Расчёт сопротивления электрических цепей
Расчёт сопротивления электрических цепей Баллистическое движение
Баллистическое движение Давление жидкостей и газов. Игра – путешествие
Давление жидкостей и газов. Игра – путешествие Тепловое действие тока. Закон Джоуля-Ленца
Тепловое действие тока. Закон Джоуля-Ленца Гибридно-волновой движитель
Гибридно-волновой движитель Радиоактивность
Радиоактивность plazma-chetvyortoe-sostoyanie-veshchestva
plazma-chetvyortoe-sostoyanie-veshchestva Качение бревна сосновых пород по наклонной плоскости с учетом сучковатости
Качение бревна сосновых пород по наклонной плоскости с учетом сучковатости Фізичні та хімічні явища
Фізичні та хімічні явища Кульова блискавка
Кульова блискавка Давление света
Давление света Электродинамика Максвелла: границы и перспективы обобщений и модификаций
Электродинамика Максвелла: границы и перспективы обобщений и модификаций Фазовые и структурные превращения в оболочках ТВЭЛов из сплава Э110 в условиях сухого хранения
Фазовые и структурные превращения в оболочках ТВЭЛов из сплава Э110 в условиях сухого хранения О науке, Земле и физике
О науке, Земле и физике Инверторные источники питания
Инверторные источники питания ДМА – динамически механический анализ
ДМА – динамически механический анализ Простые механизмы. КПД
Простые механизмы. КПД Презентация на тему Квантовая физика
Презентация на тему Квантовая физика  Презентация на тему Плавление
Презентация на тему Плавление  Лекция 2 НаучнРубрикатор
Лекция 2 НаучнРубрикатор