Совместное действие растяжения-сжатия и изгиба

Этот случай сложного сопротивления часто встречается в инженерной практике в процессе эксплуатации колонн, опор мостов, путепроводов, виадуков и других подобных строительных конструкций, обладающих малой гибкостью.
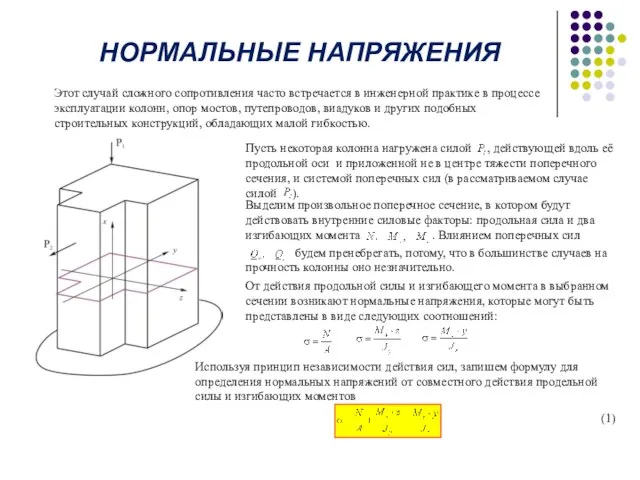
Пусть некоторая колонна нагружена силой , действующей вдоль её продольной оси и приложенной не в центре тяжести поперечного сечения, и системой поперечных сил (в рассматриваемом случае силой ).
НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ
Выделим произвольное поперечное сечение, в котором будут действовать внутренние силовые факторы: продольная сила и два изгибающих момента . Влиянием поперечных сил
будем пренебрегать, потому, что в большинстве случаев на прочность колонны оно незначительно.
От действия продольной силы и изгибающего момента в выбранном сечении возникают нормальные напряжения, которые могут быть представлены в виде следующих соотношений:
Используя принцип независимости действия сил, запишем формулу для определения нормальных напряжений от совместного действия продельной силы и изгибающих моментов
(1)

Очевидно, условие прочности балки, испытывающей косой изгиб, выполняется, если модуль максимальных нормальных напряжений, описываемых формулой (1), не будет превышать расчетного сопротивления:
УСЛОВИЕ ПРОЧНОСТИ
В процессе реализации формулы (2) важно выбрать положение опасного сечения и опасной точки.
При выборе опасного сечения учитывают максимальные значения всех внутренних силовых факторов. Если это условие реализуется в одном сечении, то оно и является опасным, если в разных, то необходимо проверить все сечения, в которых каждый из силовых факторов достигает максимальной величины.
ОПАСНАЯ ТОЧКА
Здесь: - значения продольной силы и изгибающих моментов в рассматриваемом поперечном сечении;
- соответственно, площадь и осевые моменты инерции относительно главно-центральных осей поперечного сечения;
z и y - координаты точки, в которой определяются напряжения
(2)
Как и в случае косого изгиба опасной точкой в опасном сечении будет являться точка, наиболее удаленная от нулевой линии. А нулевой линией будем называть геометрическое место точек в плоскости поперечного сечения колонны, в которых нормальные напряжения (см. равенство (1)) равны нулю.

Разделим левую и правую части этого уравнения на первое слагаемое:
Таким образом, если известны значения внутренних силовых факторов, а так же геометрические характеристики поперечного сечения, по формулам (2) определяются отрезки по осям, через которые проводят нулевую линию. Напомним, нулевая линия делит поперечное сечение на сжатую и растянутые части.
УСЛОВИЕ ПРОЧНОСТИ
Или:
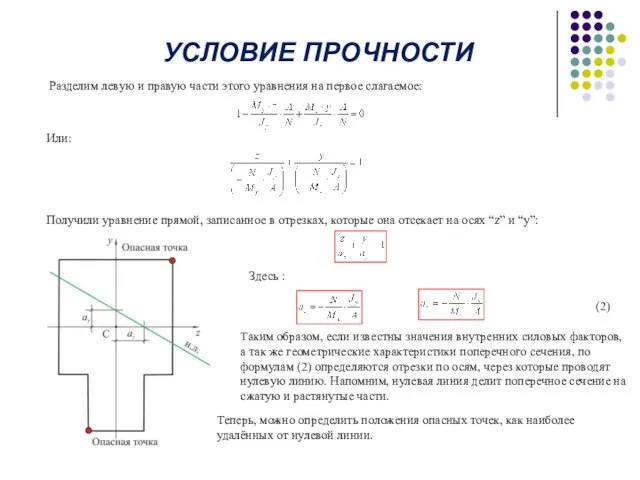
Получили уравнение прямой, записанное в отрезках, которые она отсекает на осях “z” и “y”:
Здесь :
(2)
Теперь, можно определить положения опасных точек, как наиболее удалённых от нулевой линии.

В итоге, условие прочности для колонны, находящейся в условиях совместного действия растяжения-сжатия и изгиба, может быть представлена в виде:
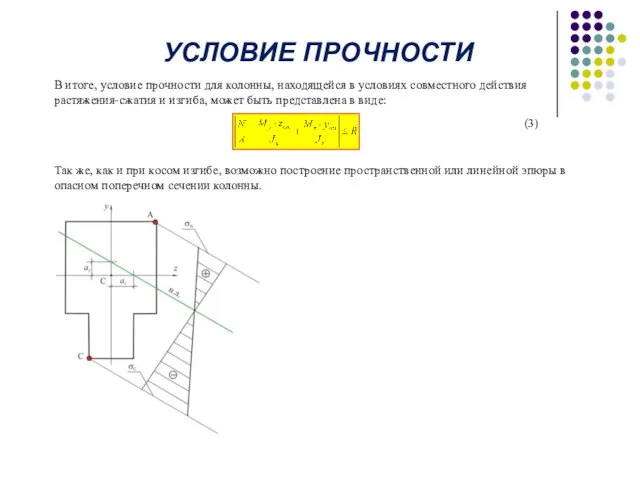
Так же, как и при косом изгибе, возможно построение пространственной или линейной эпюры в опасном поперечном сечении колонны.
(3)
УСЛОВИЕ ПРОЧНОСТИ

Пусть на колонну действует сила ”P”, которая приложена в точке, которая имеет координаты . Эту точку в дальнейшем будем называть “силовой точкой”.
Рассмотрим частный случай совместного действия растяжения (сжатия) и изгиба: на колонну действует только одна сила, которая направлена вдоль продольной оси стержня и приложена не к центре тяжести поперечного сечения.
Тогда соотношение (1) можно преобразовать к виду:
От действия такой нагрузки в любом поперечном сечении колонны будут действовать продольная сила и изгибающие моменты:
ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ
(СЖАТИЕ) КОЛОННЫ
Введем понятия радиусов инерции:
и получим окончательно
(4)