Содержание
- 2. План Механика: Кинематика. 1. Механическое движение. Относительность механического движения. Материальная точка. Система отсчета. Траектория. Вектор перемещения
- 3. Кинематика Механическое движение – изменение положения тела или частей тела в пространстве относительно других тел с
- 4. Кинематика Механика делится на кинематику и динамику. В кинематике изучают движения тел, не рассматривая причин, определяющих
- 5. Кинематика Материальная точка – тело, размерами которого в данной задаче можно пренебречь. Чтобы решить задачу о
- 6. Задание положения точки с помощью координат Система координат – три взаимно перпендикулярные оси OX, OY, OZ
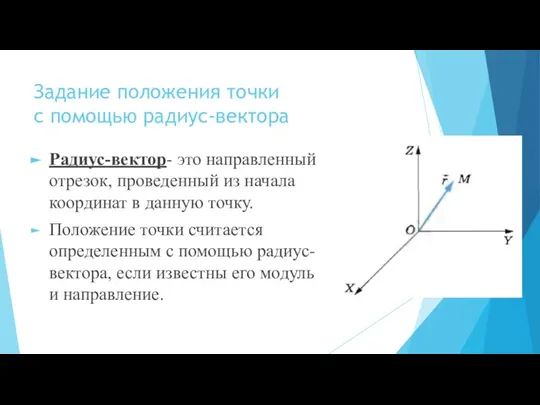
- 7. Задание положения точки с помощью радиус-вектора Радиус-вектор- это направленный отрезок, проведенный из начала координат в данную
- 8. Кинематика Проекция вектора на ось – длина отрезка A1B1 между проекциями начала и конца вектора на
- 9. Кинематика Если тело можно считать материальной точкой, то для описания его движения нужно уметь рассчитать положение
- 10. Кинематика Координатный способ – т.к. материальная точка движется, то ее координаты изменяются с течением времени: x
- 11. Кинематика Линия по которой движется точка в пространстве называется траекторией. Если траекторией является прямая линия –
- 12. Кинематика Система отсчета – тело отсчета, система координат, связанная с ним и часы. Вектор перемещения (перемещение)
- 13. Кинематика Путь l, пройденный материально точкой за время t – длина отрезка траектории между начальным и
- 14. Кинематика Равномерное прямолинейное движение – движение, при котором м.т. за любые равные промежутки времени совершает одинаковые
- 15. Кинематика Это уравнение равномерного прямолинейного движения м.т., записанное в векторной форме. Это уравнение равномерного прямолинейного движения
- 16. Графическое представление равномерного прямолинейного движения Площадь прямоугольника равна пути X0 – различные Т.к. скорость численно равна
- 17. Неравномерное движение Неравномерное движение может быть как прямолинейным, так и криволинейным. Чтобы описать неравномерное движение точки,
- 18. Неравномерное движение Если точка перемещается из положения М в М1, двигаясь невномерно и криволинейно, то она
- 19. Неравномерное движение Средняя путевая скорость – отношение пути к промежутку времени, за которое этот путь пройден.
- 20. Кинематика Пусть река течет относительно берега со скоростью v. По реке плывет моторная лодка со скоростью
- 21. Кинематика Закон сложения скоростей: если тело движется относительно некоторой системы отсчета К1 со скоростью v1 и
- 22. Основная литература Физика: Механика. 10 кл.: Учебник для углубленного изучения физики /Под ред. Г.Я.Мякишева. - М.:
- 24. Скачать презентацию




















 Конструкционные материалы. Классификация. Свойства
Конструкционные материалы. Классификация. Свойства Уравнения материального баланса. Уравнение Бернулли, уравнение неразрывности
Уравнения материального баланса. Уравнение Бернулли, уравнение неразрывности Презентация по физике "Оптические иллюзии или Обман зрения" -
Презентация по физике "Оптические иллюзии или Обман зрения" -  Законы сохранения в механике
Законы сохранения в механике Равновесие. Ключевые слова
Равновесие. Ключевые слова Сверхпроводимость. Свойства
Сверхпроводимость. Свойства Pезонанс прояви і застосування
Pезонанс прояви і застосування Тезаурус ВВЭР поколения 3+
Тезаурус ВВЭР поколения 3+ Ток проводимости в металлах, его характеристики и условия существования
Ток проводимости в металлах, его характеристики и условия существования Курс физики. Введение
Курс физики. Введение Эксперимент политропного расширения воздуха (Кафедра теплотехники. Лабораторная работа №1)
Эксперимент политропного расширения воздуха (Кафедра теплотехники. Лабораторная работа №1) Теплоприемник. Упрощение устройства при одновременном повышении точности измерения
Теплоприемник. Упрощение устройства при одновременном повышении точности измерения Излучение электромагнитного поля. Антенны
Излучение электромагнитного поля. Антенны Источники звука. Звуковые колебания
Источники звука. Звуковые колебания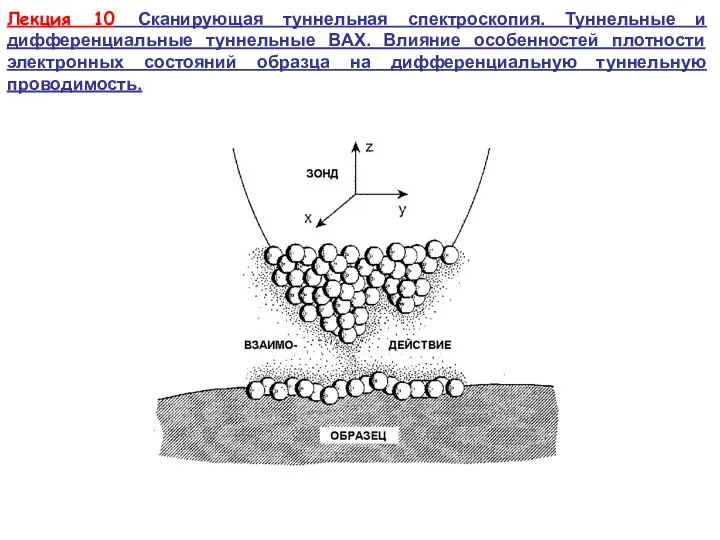 Сканирующая туннельная спектроскопия. Туннельные и дифференциальные туннельные ВАХ
Сканирующая туннельная спектроскопия. Туннельные и дифференциальные туннельные ВАХ Спектроскопия
Спектроскопия Решение задач на движение по наклонной плоскости
Решение задач на движение по наклонной плоскости Баллистическое движение
Баллистическое движение Упругие механические волны. Уравнение бегущей и стоячей волны
Упругие механические волны. Уравнение бегущей и стоячей волны Способы изготовление байдарки
Способы изготовление байдарки Инфракра́сное излуче́ние
Инфракра́сное излуче́ние Презентация на тему Электрическое поле
Презентация на тему Электрическое поле  Судовые двигатели внутреннего сгорания. Лекция 11
Судовые двигатели внутреннего сгорания. Лекция 11 Кинематический анализ рычажного механизма. План скоростей. Практика №3
Кинематический анализ рычажного механизма. План скоростей. Практика №3 Презентация на тему История создания тепловых двигателей
Презентация на тему История создания тепловых двигателей  Опиливание заготовок из металла и пластмассы
Опиливание заготовок из металла и пластмассы Изучение звуковых колебаний
Изучение звуковых колебаний Виды излучений и спектров. Шкала электромагнитных волн
Виды излучений и спектров. Шкала электромагнитных волн