Лекция 25

Основные характеристики дифракционной решетки как спектрального прибора:
Угловая дисперсия . Она характеризует изменение угла дифракции с
изменением длины волны. Ее величина обычно находится дифференцированием
по длине волны от условия главных максимумов. В случае перпендикулярного падения
волны на решетку
На практике обычно наблюдается спектр, относящийся к первому максимуму
(«спектр первого порядка»), поэтому формула для угловой дисперсии
записывается в виде

2. Разрешающая способность определяет возможность реального разрешения (разделения) двух близких максимумов одного порядка, получающихся для разных длин волн.
Рэлей предложил следующий критерий спектрального разрешения. Спектральные линии с близкими длинами волн считаются разрешенными, если главный максимум дифракционной картины для одной длины волны λ совпадает по своему положению с ближайшим дифракционным минимумом картины для другой длины волны λ+dλ .
Для критерия Релея можно записать

Отсюда следует, что для повышения разрешающей способности дифракционной
решетки необходимо либо повышать порядок дифракционного максимума m,
используемый для наблюдения спектра, либо увеличивать число щелей решетки N.

Дифракционное уширение.
Пусть у нас есть узкая щель, на которую падает плоская монохроматическая волна. На экране будет наблюдаться дифракционная картина в виде чередующихся светлых и темных полос. Точка первого минимума интенсивности на экране наблюдения будет под углом λ/b. Если рассматривать нулевой максимум как искаженное изображение щели, то получится, что это изображение больше, чем сама щель.

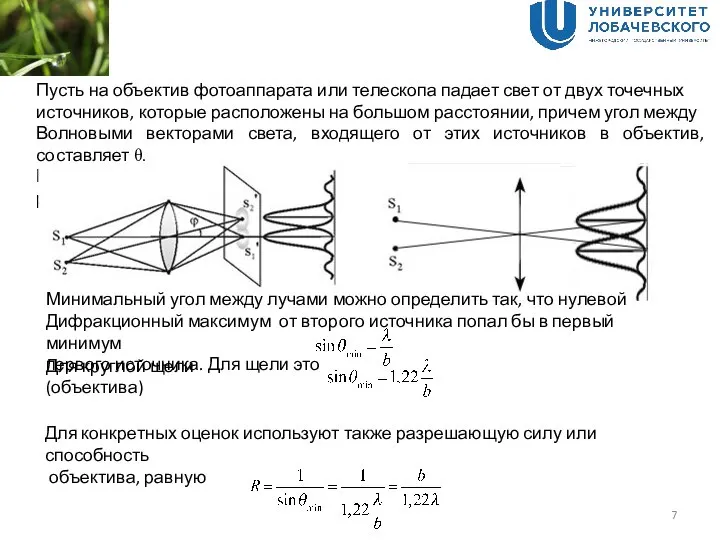
Это явление увеличения изображения называется дифракционным уширением, которое является следствием волновой природы света. Оно не устранимо в принципе, т.к. не устранима волновая природа света. Минимальный угол, при котором может наблюдаться какая-либо структура изображения щели
Для круглой щели можно получить условие
При b>>λ λ/b стремится к нулю и дифракционное уширение становится незначительным, и можно считать, что работает геометрическая оптика.
Сделаем некоторые оценки:
1. Труба b=10см, λ=0,63 мкм. θmin равен приблизительно 1’’.
2. Телескоп с диаметром объектива 6м. Тогда θmin равен приблизительно 0,02’’.
3. Человеческий глаз b=4мм
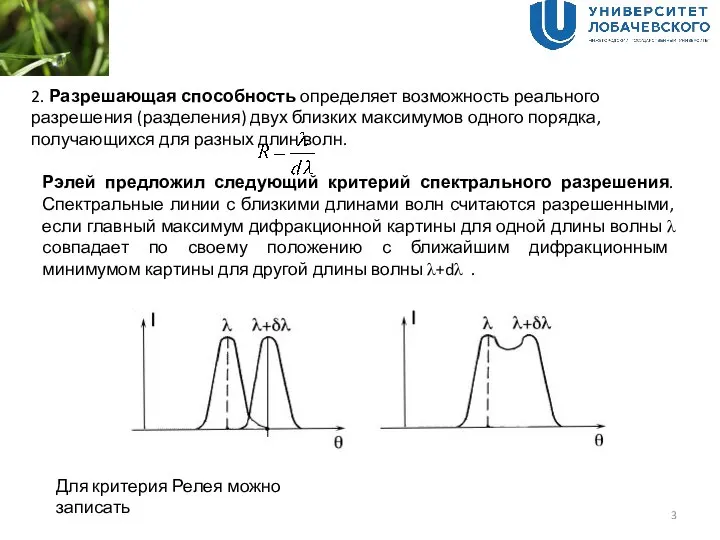
Это минимальное угловое расстояние между, например, звездами, которое
в принципе можно рассмотреть в данный телескоп. Никакими способами
Улучшить этот предел нельзя, можно только повышать диаметр объектива.

Пусть на объектив фотоаппарата или телескопа падает свет от двух точечных
источников, которые расположены на большом расстоянии, причем угол между
Волновыми векторами света, входящего от этих источников в объектив, составляет θ.
Найдем минимальный угол dθ, при котором эти два источника еще можно различить.
Минимальный угол между лучами можно определить так, что нулевой
Дифракционный максимум от второго источника попал бы в первый минимум
первого источника. Для щели это
Для круглой щели (объектива)
Для конкретных оценок используют также разрешающую силу или способность
объектива, равную