Магнитное поле в веществе

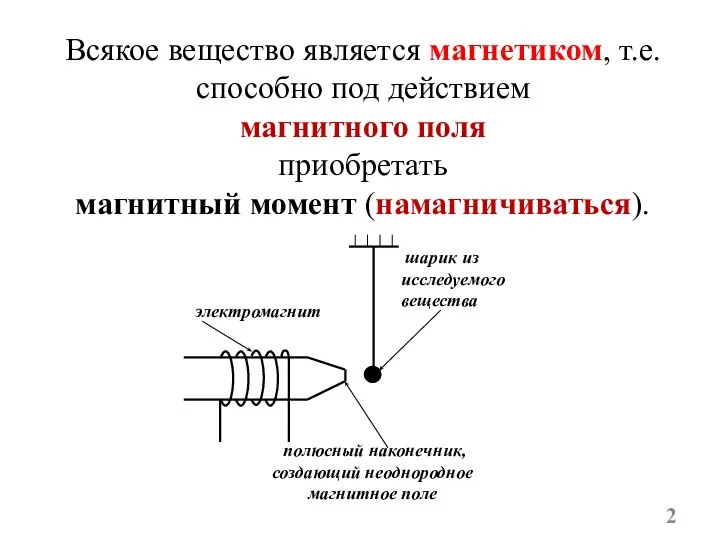
Всякое вещество является магнетиком, т.е. способно под действием
магнитного поля
приобретать
магнитный момент (намагничиваться).

Всякая среда при внесении её во внешнее магнитное поле намагничивается
в той или иной степени,
т.е. создаёт своё
собственное магнитное поле,
накладывающееся на внешнее поле.

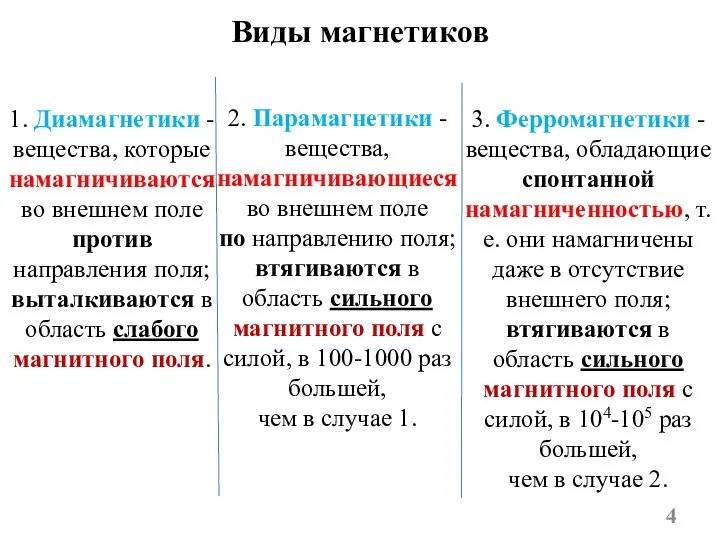
Виды магнетиков
1. Диамагнетики - вещества, которые намагничиваются во внешнем поле против направления поля; выталкиваются в область слабого магнитного поля.
2. Парамагнетики - вещества, намагничивающиеся во внешнем поле
по направлению поля; втягиваются в область сильного магнитного поля с силой, в 100-1000 раз большей,
чем в случае 1.
3. Ферромагнетики - вещества, обладающие спонтанной намагниченностью, т.е. они намагничены даже в отсутствие внешнего поля; втягиваются в область сильного магнитного поля с силой, в 104-105 раз большей,
чем в случае 2.

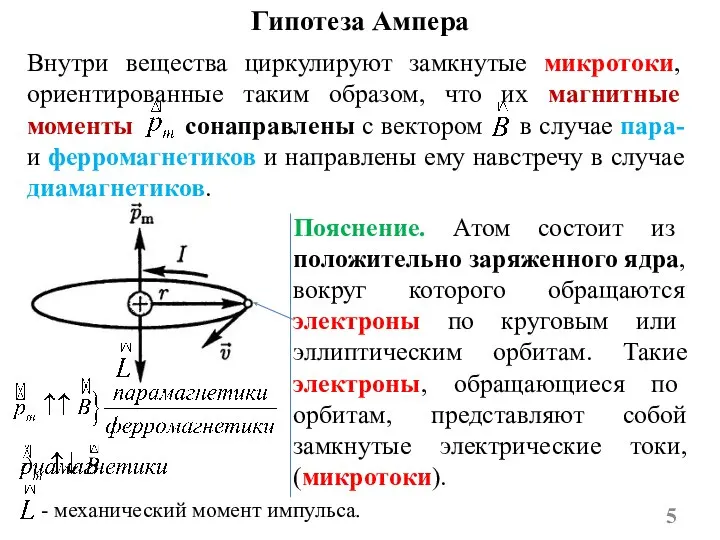
Гипотеза Ампера
Внутри вещества циркулируют замкнутые микротоки, ориентированные таким образом, что их магнитные моменты сонаправлены с вектором в случае пара- и ферромагнетиков и направлены ему навстречу в случае диамагнетиков.
Пояснение. Атом состоит из положительно заряженного ядра, вокруг которого обращаются электроны по круговым или эллиптическим орбитам. Такие электроны, обращающиеся по орбитам, представляют собой замкнутые электрические токи, (микротоки).
- механический момент импульса.

Если электрон совершает ν оборотов в секунду, то сила тока
Магнитный момент электрона, движущегося по круговой орбите, площадью S
Если электрон движется по часовой стрелке, то ток I направлен против часовой стрелки и вектор
(в соответствии с правилом правого винта) направлен перпендикулярно плоскости орбиты электрона.

Вектор напряжённости магнитного поля
Макроскопические токи – электрические токи, протекающие по проводникам в электрических цепях.
Микроскопические токи – электрические токи, обусловленные движением электронов в атомах и молекулах. Эти токи создают своё магнитное поле и могут поворачиваться в магнитных полях макротоков.
Магнитное поле макротока описывается вектором напряжённости магнитного поля
Вектор магнитной индукции характеризует РЕЗУЛЬТИРУЮЩЕЕ магнитное поле, создаваемое всеми макро- и микротоками.

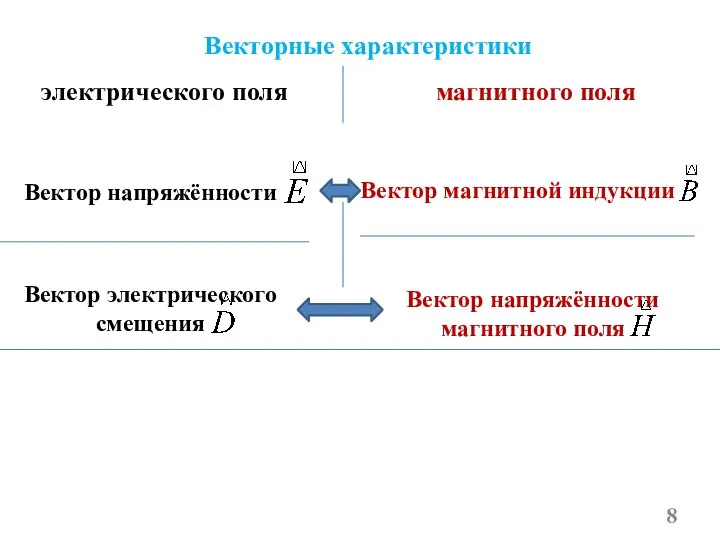
электрического поля
магнитного поля
Векторные характеристики
Вектор напряжённости
Вектор магнитной индукции
Вектор электрического смещения
Вектор напряжённости магнитного поля

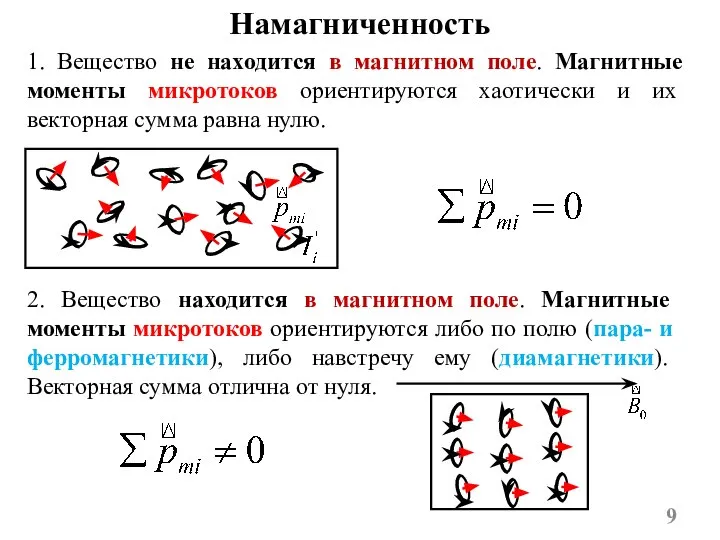
Намагниченность
1. Вещество не находится в магнитном поле. Магнитные моменты микротоков ориентируются хаотически и их векторная сумма равна нулю.
2. Вещество находится в магнитном поле. Магнитные моменты микротоков ориентируются либо по полю (пара- и ферромагнетики), либо навстречу ему (диамагнетики). Векторная сумма отлична от нуля.

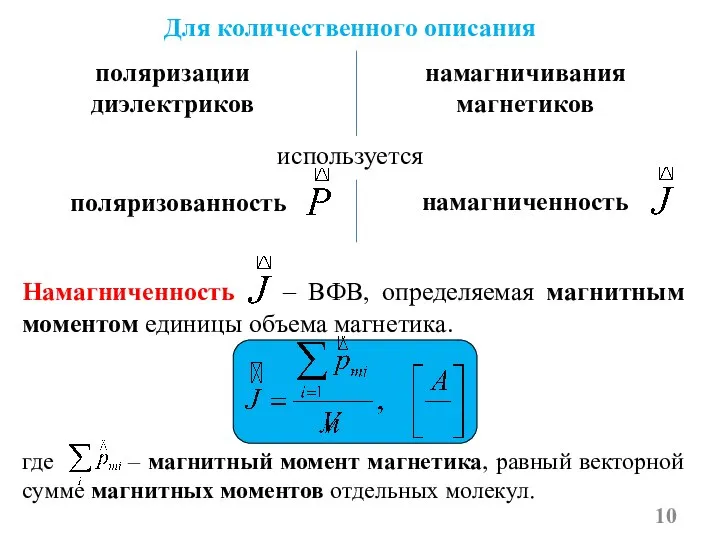
Намагниченность – ВФВ, определяемая магнитным моментом единицы объема магнетика.
Для количественного описания
поляризации диэлектриков
намагничивания магнетиков
используется
поляризованность
намагниченность
где – магнитный момент магнетика, равный векторной сумме магнитных моментов отдельных молекул.

Отметим: В несильных полях для неферромагнитных веществ намагниченность пропорциональна напряжённости магнитного поля, вызывающего намагничивание.
для диамагнетиков χ отрицательна
(χ<0: поле молекулярных токов противоположно внешнему полю),
для парамагнетиков χ – положительна
(χ>0: поле молекулярных токов совпадает с внешним).
где χ – безразмерная величина.
Диамагнетики χ: -(10-6 – 10-5).
Парамагнетики χ: 10-2 – 10-4.

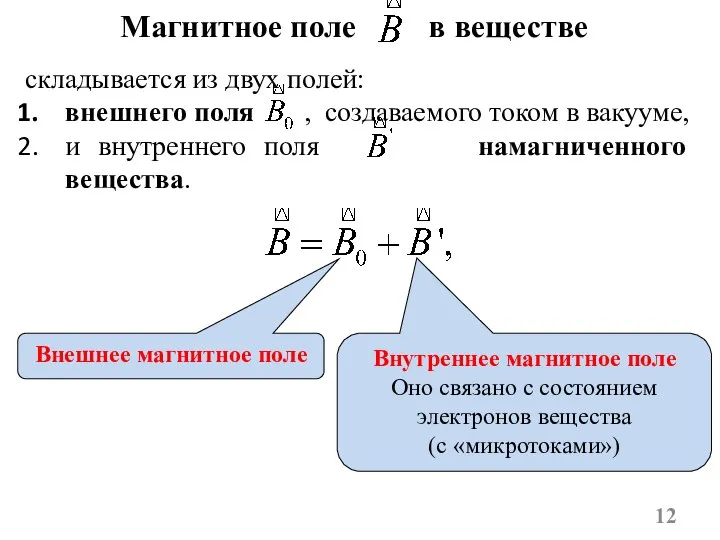
Магнитное поле в веществе
складывается из двух полей:
внешнего поля , создаваемого током в вакууме,
и внутреннего поля намагниченного вещества.
Внешнее магнитное поле
Внутреннее магнитное поле
Оно связано с состоянием электронов вещества
(с «микротоками»)

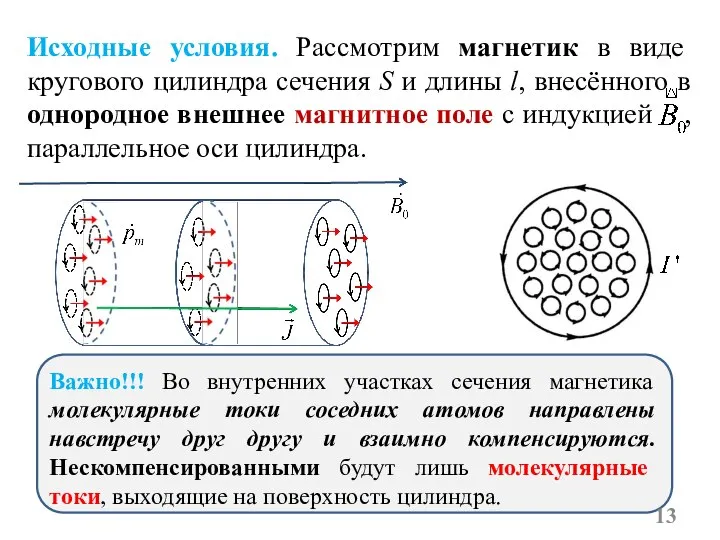
Исходные условия. Рассмотрим магнетик в виде кругового цилиндра сечения S и длины l, внесённого в однородное внешнее магнитное поле с индукцией , параллельное оси цилиндра.
Важно!!! Во внутренних участках сечения магнетика молекулярные токи соседних атомов направлены навстречу друг другу и взаимно компенсируются. Нескомпенсированными будут лишь молекулярные токи, выходящие на поверхность цилиндра.

Вычислим магнитную индукцию B' тока I', текущего по боковой поверхности цилиндра:
Магнитный момент этого суммарного тока микротоков внутри магнетика
где V – объём магнетика.
Намагниченность магнетика
Следовательно,
или в векторной форме

Ведём вспомогательную величину – напряжённость магнитного поля
Таким образом,
диамагнетики
парамагнетики
ферромагнетики
μ<1;
μ>1;
μ>>1
μ - магнитная проницаемость вещества

Итак, магнитная индукция внутри цилиндра станет равным
Напряжённость магнитного поля внутри цилиндра
- напряжённость магнитного поля внутри цилиндра совпадает с напряжённостью внешнего поля.
μ - магнитная проницаемость вещества показывает, во сколько раз усиливается поле в магнетике.

Закон полного тока для
магнитного поля в веществе
Этот закон является обобщением закона полного тока для магнитного поля в вакууме.
Теорема о циркуляции вектора : циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна алгебраической сумме токов проводимости и молекулярных токов, охватываемых этим контуром, умноженной на магнитную постоянную
где и – соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых произвольным замкнутым контуром L.

Циркуляция намагниченности по произвольному замкнутому контуру L равна алгебраической сумме молекулярных токов , охватываемых этим контуром:
Теорема о циркуляции вектора намагниченности

Циркуляция вектора по произвольному замкнутому контуру L равна алгебраической сумме токов проводимости , охватываемых этим контуром:
Разделим на μ0:
Воспользуемся равенством (2):
Теорема о циркуляции вектора напряжённости магнитного поля

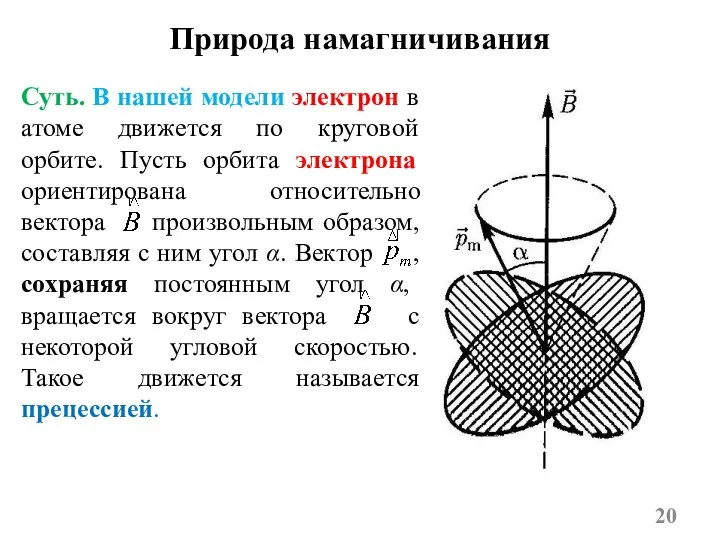
Природа намагничивания
Суть. В нашей модели электрон в атоме движется по круговой орбите. Пусть орбита электрона ориентирована относительно вектора произвольным образом, составляя с ним угол α. Вектор , сохраняя постоянным угол α, вращается вокруг вектора с некоторой угловой скоростью. Такое движется называется прецессией.

Таким образом,
электронные орбиты атома
под действием
внешнего магнитного поля совершают
прецессионное движение, которое эквивалентно
круговому току.

Свойства магнетиков
I. Диамагнетики
Представители: Bi (висмут), Ag (серебро), Au (золото), Cu (медь), органические соединения, углерод, инертные газы, глицерин.
Суть. Магнитные моменты атомов, молекул или ионов в отсутствие внешнего магнитного поля равны нулю.
При включении магнитного поля появляются наведённые магнитные моменты атомов (молекул), которые пропорциональны вектору и противоположны ему по направлению.

II. Парамагнетики
Представители: O2 (кислород), NO (оксид азота), редкоземельные металлы, MnO (оксид марганца),
Pt (платина), Al (алюминий).
Суть. Атомы парамагнетика обладают собственным магнитным моментом pm в отсутствие внешнего магнитного поля;
парамагнетик не намагничен, т.к. из-за теплового движения собственные магнитные моменты атомов ориентированы совершенно беспорядочно.

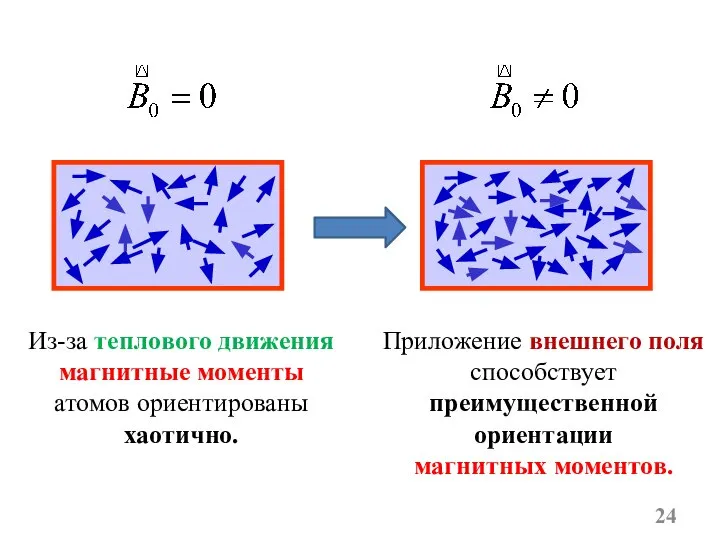
Из-за теплового движения магнитные моменты атомов ориентированы хаотично.
Приложение внешнего поля способствует преимущественной ориентации
магнитных моментов.

Итог. Совместное действие на атомы (молекулы) парамагнетика магнитного поля и столкновений их друг с другом вследствие теплового движения приводит к преимущественной ориентации собственных магнитных моментов атомов по направлению вектора .
В результате парамагнетик намагничивается «по полю», т.е. в направлении
Парамагнетик намагничивается, создавая собственное магнитное поле, усиливая внешнее поле.

При ослаблении внешнего магнитного поля до нуля ориентация магнитных моментов вследствие теплового движения нарушается и парамагнетик размагничивается.
1. Атомы всех веществ являются носителями диамагнитных свойств.
Важно!
2. Если магнитный момент атомов велик, то парамагнитные свойства преобладают над диамагнитными и вещество является парамагнетиком; 3. Если магнитный момент атомов мал, то преобладают диамагнитные свойства и вещество является диамагнетиком.

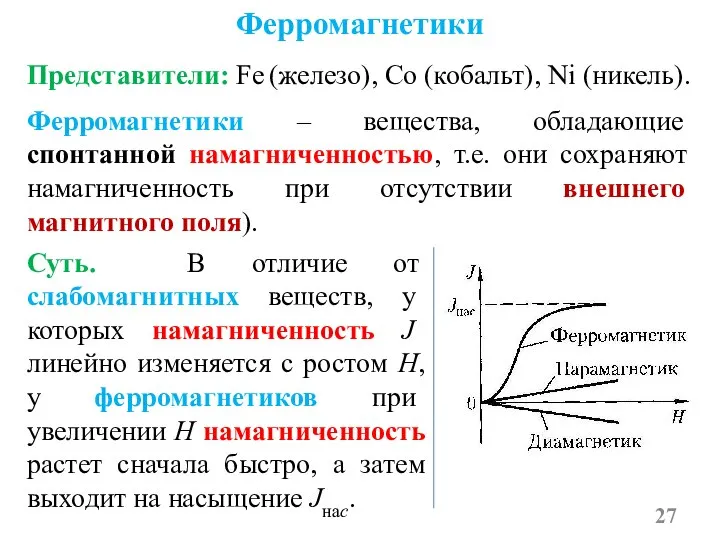
Ферромагнетики
Представители: Fe (железо), Co (кобальт), Ni (никель).
Суть. В отличие от слабомагнитных веществ, у которых намагниченность J линейно изменяется с ростом H, у ферромагнетиков при увеличении H намагниченность растет сначала быстро, а затем выходит на насыщение Jнас.
Ферромагнетики – вещества, обладающие спонтанной намагниченностью, т.е. они сохраняют намагниченность при отсутствии внешнего магнитного поля).

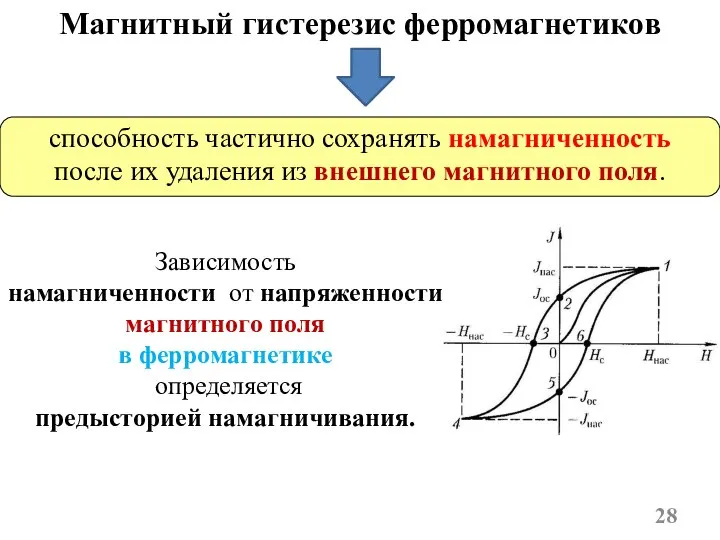
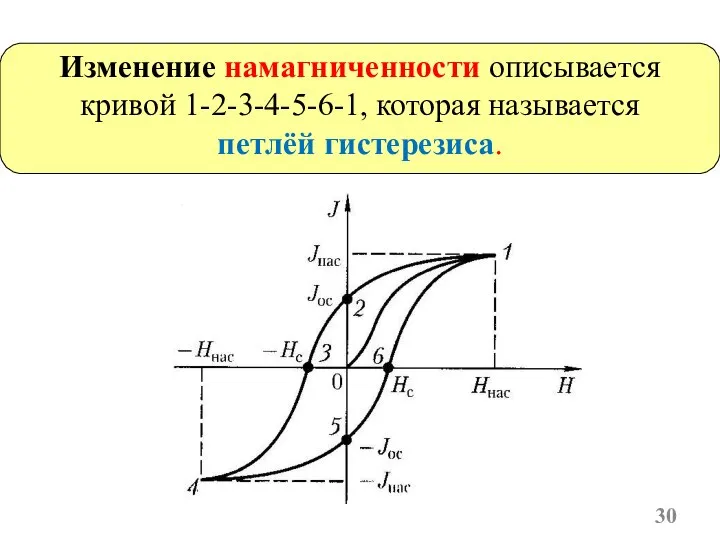
Магнитный гистерезис ферромагнетиков
способность частично сохранять намагниченность после их удаления из внешнего магнитного поля.
Зависимость
намагниченности от напряженности
магнитного поля
в ферромагнетике
определяется
предысторией намагничивания.

2. Для того чтобы уменьшить намагниченность до нуля, надо приложить противоположно направленное поле (точка 3) с напряженностью Hc, которая называется коэрцитивная сила.
Описание явления. 1. Если ферромагнетик намагнитить до насыщения (кривая 0-1), а затем уменьшать H (кривая 1-2), то при H=0 в ферромагнетике останется остаточная намагниченность Jост.
3. При дальнейшем увеличении противоположного поля ферромагнетик перемагничивается (кривая 3-4), достигая насыщения (точка 4). Затем его можно опять размагнитить (кривая 4-5-6) и вновь перемагнитить до насыщения (кривая 6-1).

Изменение намагниченности описывается
кривой 1-2-3-4-5-6-1, которая называется
петлёй гистерезиса.

Температура Кюри
Точка Кюри – температура, при которой ферромагнетик теряет свои магнитные свойства.
При нагревании выше точки Кюри ферромагнетик превращается в обычный парамагнетик.
Описание явления. Причина такого поведения в том, что при температурах ниже точки Кюри ферромагнетик разбивается на большое число микроскопических областей – доменов, самопроизвольно намагниченных до насыщения.

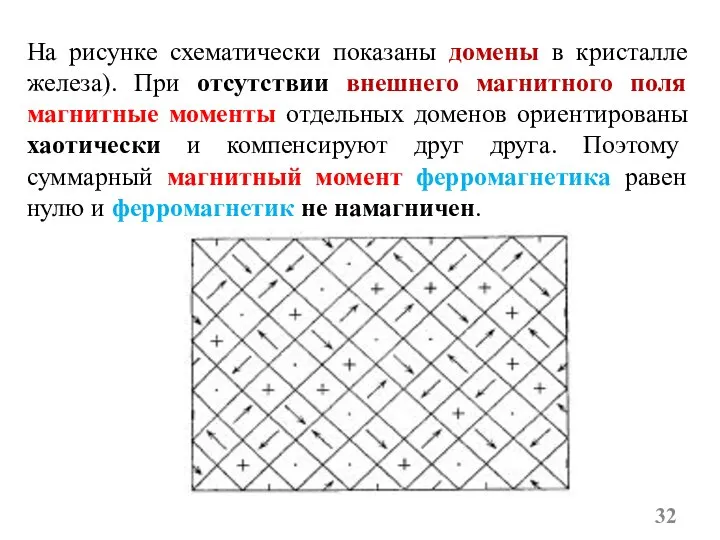
На рисунке схематически показаны домены в кристалле железа). При отсутствии внешнего магнитного поля магнитные моменты отдельных доменов ориентированы хаотически и компенсируют друг друга. Поэтому суммарный магнитный момент ферромагнетика равен нулю и ферромагнетик не намагничен.

Внешнее поле ориентирует по полю магнитные моменты целых областей спонтанной намагниченности, причем домены поворачиваются по полю скачком.
Точка Кюри – температура, выше которой происходит разрушение доменной структуры.