Содержание
- 2. МАТЕМАТИЧЕСКАЯ СПРАВКА Большинство реальных колебательных процессов не являются строго периодическими. Однако, экспериментально любые сложные колебания можно
- 3. Теоретически сложные колебания можно представить с помощью рядов (и интегралов) Фурье. Согласно теореме Ж. Фурье (1822
- 4. Согласно теории рядов Фурье, всякая периодическая функция f(t), ограниченная на отрезке и имеющая конечное число экстремумов
- 5. Для четной функции f(-t)= f(t) все коэффициенты ак равны нулю. Для нечетной ф -ии f(-t)= -
- 6. Для решения этой задачи могут использоваться комплексные ряды Фурье в виде: ( 5 ) где п
- 7. В разложении (5) представлен дискретный спектр частот: Непериодическая функция f(t) представляется в виде комплексного интеграла Фурье:
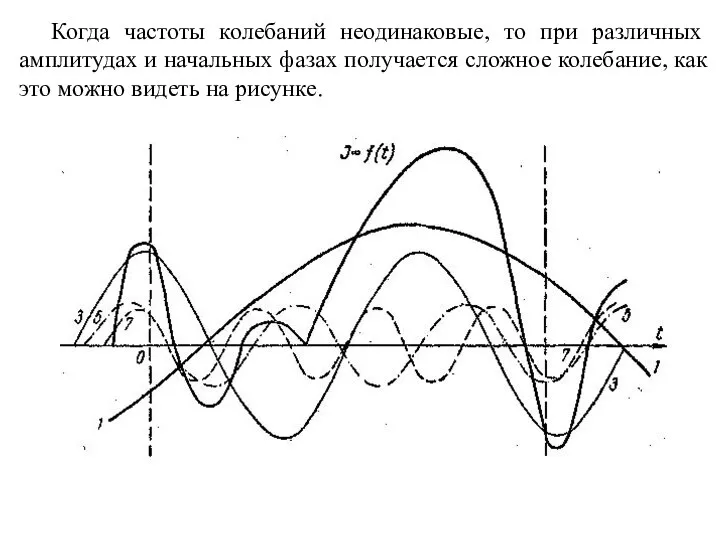
- 8. Когда частоты колебаний неодинаковые, то при различных амплитудах и начальных фазах получается сложное колебание, как это
- 9. Разложение сложного колебательного движения на составляющие простые гармоники с кратными частотами: 1—1,— основная гармоника ( β1
- 10. По теореме Фурье любую периодическую функцию можно представить в виде суммы нескольких гармонических функций с кратными
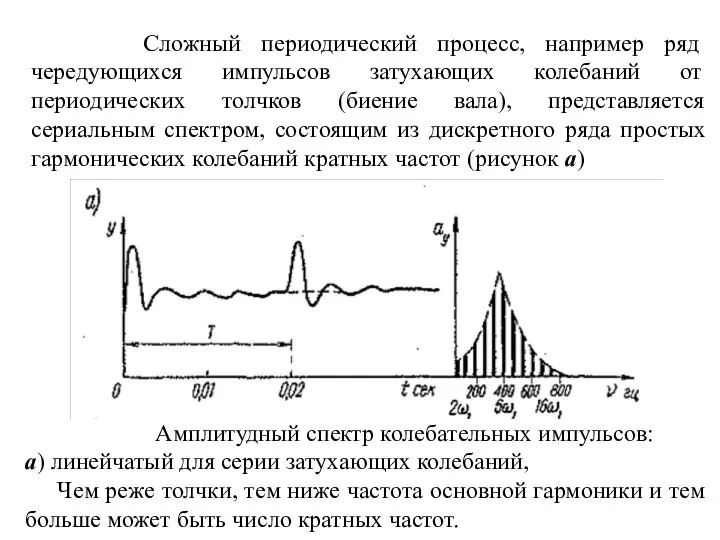
- 11. Сложный периодический процесс, например ряд чередующихся импульсов затухающих колебаний от периодических толчков (биение вала), представляется сериальным
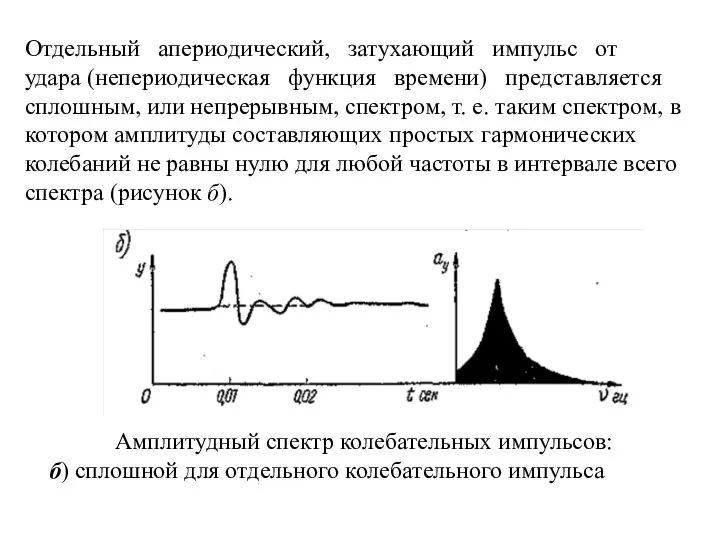
- 12. Отдельный апериодический, затухающий импульс от удара (непериодическая функция времени) представляется сплошным, или непрерывным, спектром, т. е.
- 13. В зависимости от характера воздействия, вызывающего и поддерживающего колебательный процесс, колебания классифицируют как свободные (или собственные),
- 14. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ Гармонические колебания представляют собой наиболее простой вид колебаний. Пусть х — динамическая переменная, характеризующая
- 15. А — амплитуда колебаний, т. е. наибольшее положительное отклонение величины х от ее значения в состоянии
- 16. Величины ϕ = ωt +ϕ01 и ϕ = ωt +ϕ02 называются фазами колебаний. Фаза характеризует текущее
- 17. Произвольное гармоническое колебание может быть представлено и иным образом. Преобразуем ,например, х = Аsin (ωt +
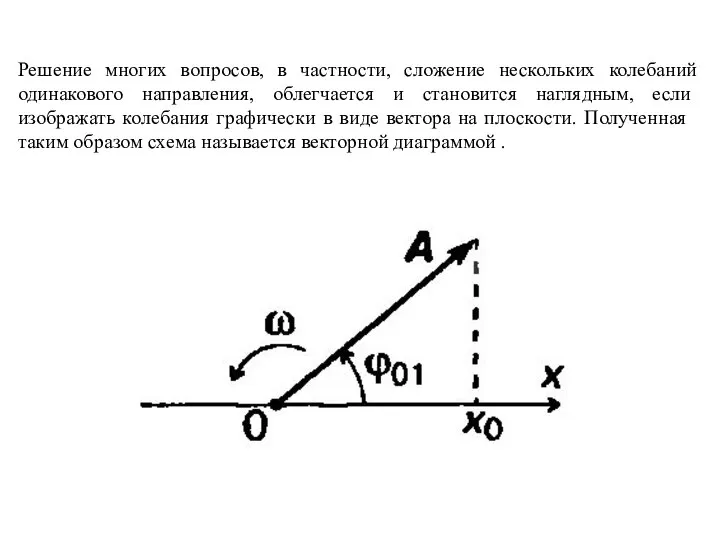
- 19. Решение многих вопросов, в частности, сложение нескольких колебаний одинакового направления, облегчается и становится наглядным, если изображать
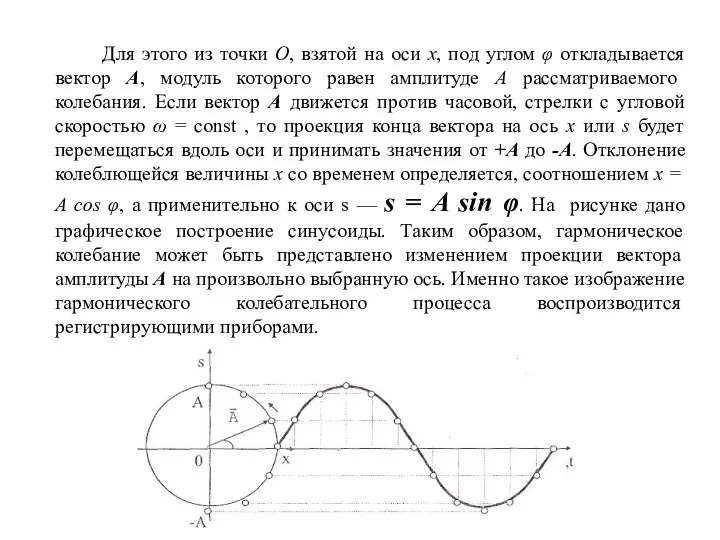
- 20. Для этого из точки О, взятой на оси х, под углом φ откладывается вектор А, модуль
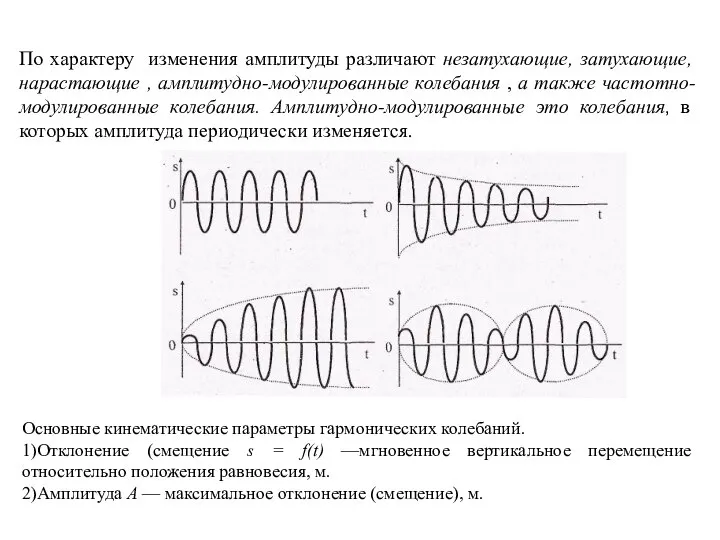
- 21. По характеру изменения амплитуды различают незатухающие, затухающие, нарастающие , амплитудно-модулированные колебания , а также частотно-модулированные колебания.
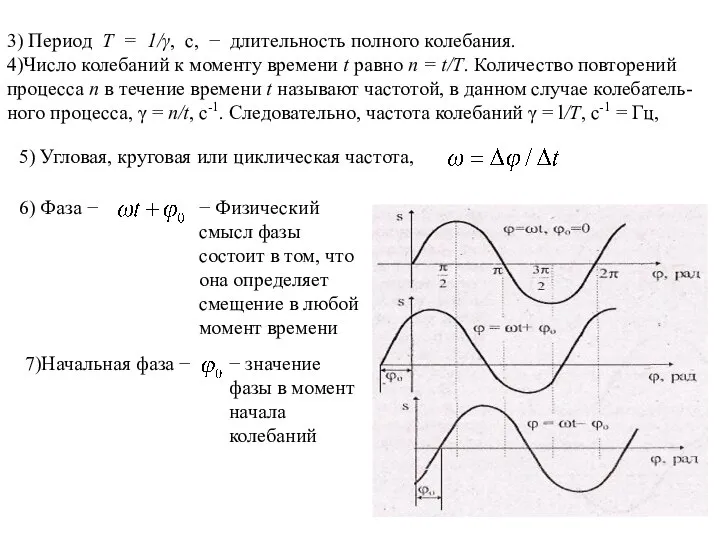
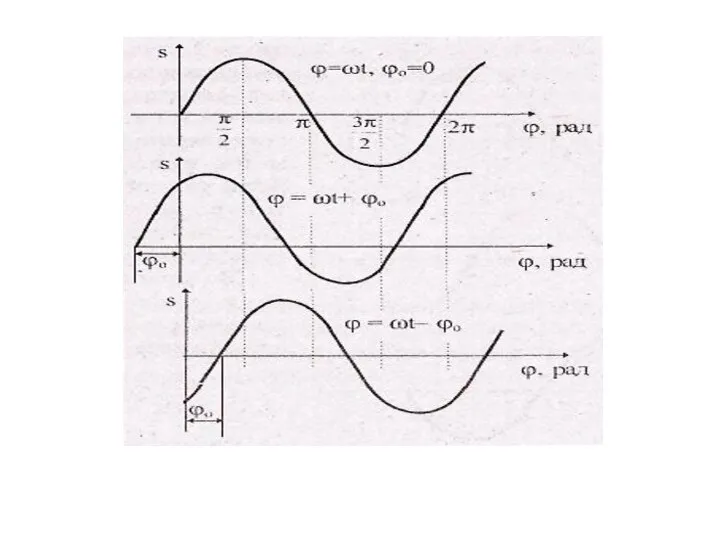
- 22. 3) Период Т = 1/γ, с, − длительность полного колебания. 4)Число колебаний к моменту времени t
- 24. Для гармонического движения системы мгновенная скорость Мгновенное ускорение колебательной системы определяется второй производной s = Acosφ
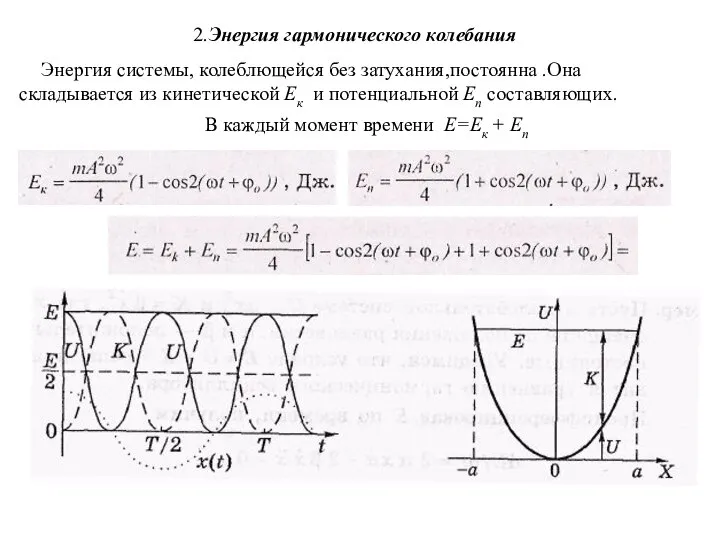
- 25. 2.Энергия гармонического колебания Энергия системы, колеблющейся без затухания,постоянна .Она складывается из кинетической Ек и потенциальной Еп
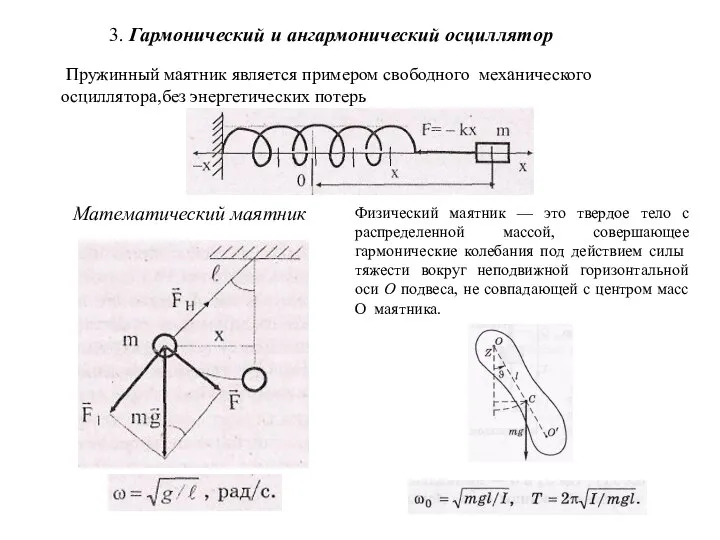
- 26. 3. Гармонический и ангармонический осциллятор Пружинный маятник является примером свободного механического осциллятора,без энергетических потерь Математический маятник
- 27. Наряду с гармоническим осциллятором существует понятие ангармонического (нелинейного) осциллятора. Его колебания отличаются от гармонических. Их основная
- 28. Разность фаз δ не зависит от времени и равна
- 29. Когда |ω1–ω2| Результирующее колебание, с медленно и периодически меняющейся амплитудой, называется биения. Амплитуда колебаний описывается формулой
- 30. Промежуток времени между соседними моментами, когда амплитуда а максимальна , называют периодом биений τ б. За
- 31. 2)Сложение взаимно перпендикулярных колебаний одинаковой частоты
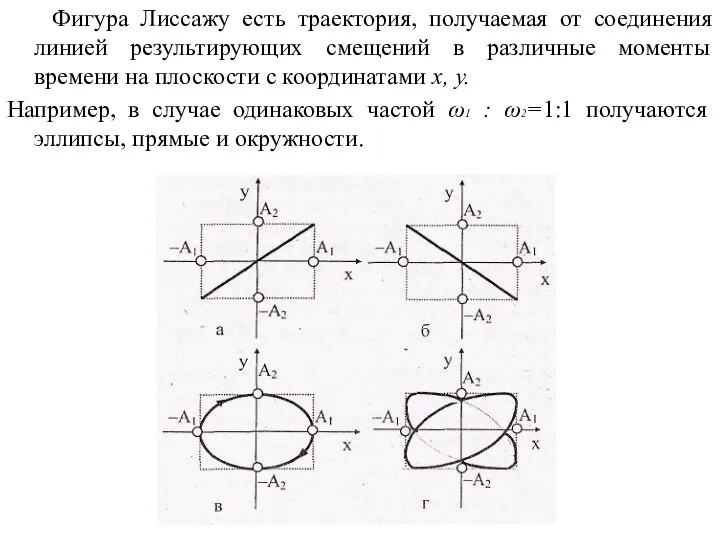
- 32. Фигура Лиссажу есть траектория, получаемая от соединения линией результирующих смещений в различные моменты времени на плоскости
- 33. Если частоты взаимно перпендикулярных колебаний не одинаковы и относятся как целые числа, то траектории результирующего движения
- 34. Фигуры Ж. Лиссажу можно наблюдать при подаче на пластины осциллографа двух электрических сигналов, один из которых
- 35. При сложении взаимно-перпендикулярных колебаний полная энергия т. е. складывается из энергий каждого колебания (в отличие от
- 36. Fx= – r , Из основного уравнения динамики следует, что на частицу массы m действует кроме
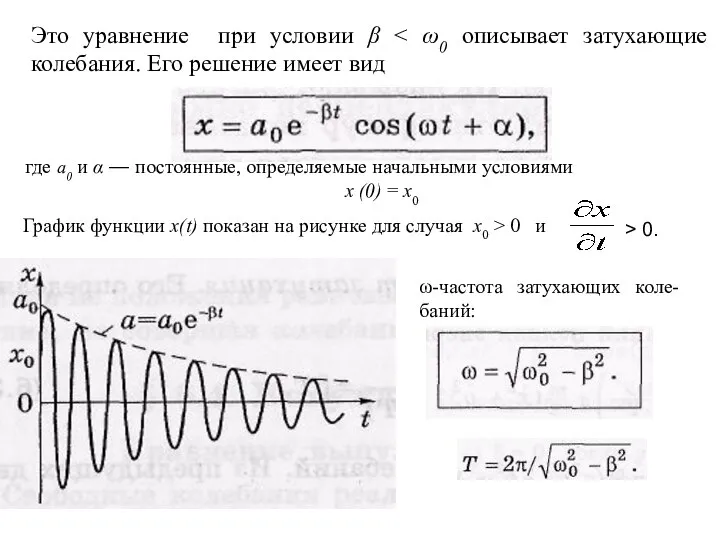
- 37. Это уравнение при условии β где а0 и α — постоянные, определяемые начальными условиями х (0)
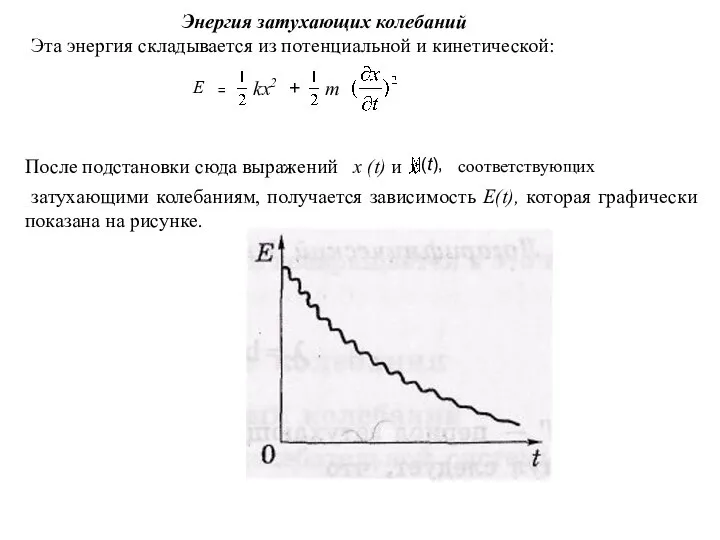
- 38. Энергия затухающих колебаний Эта энергия складывается из потенциальной и кинетической: После подстановки сюда выражений х (t)
- 39. Характеристики затухания. Кроме коэффициента β , затухание колебаний характеризуют величинами: 1) Время релаксации — это время,
- 40. 3) Добротность осциллятора − При малом затухании β«ω0 добротность равна Логарифмический декремент затухания λ (при малом
- 41. Вынужденные колебания.Уравнение вынужденных колебаний Потери энергии, обусловленные силами сопротивления (трения), можно компенсировать, воздействуя на систему переменной
- 42. Если на колеблющуюся частицу будут действовать одновременно три силы:квазиупруггая ( − kx ), сила сопротивления (
- 43. Опыт показывает, что по истечении некоторого времени с момента начала действия вынуждающей силы в системе устанавливаются
- 44. Учитывая фазовые сдвиги между х, и , представим это равенство с помощью векторной диаграммы для случая
- 45. по теореме Пифагора =
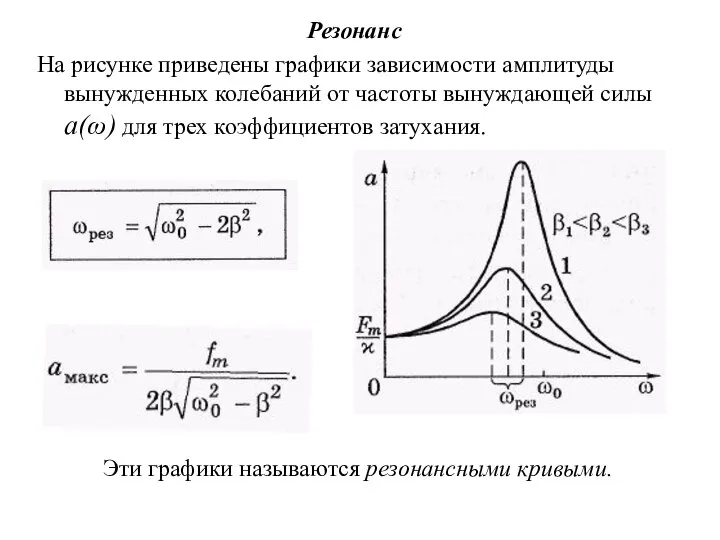
- 46. Резонанс На рисунке приведены графики зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы а(ω) для трех
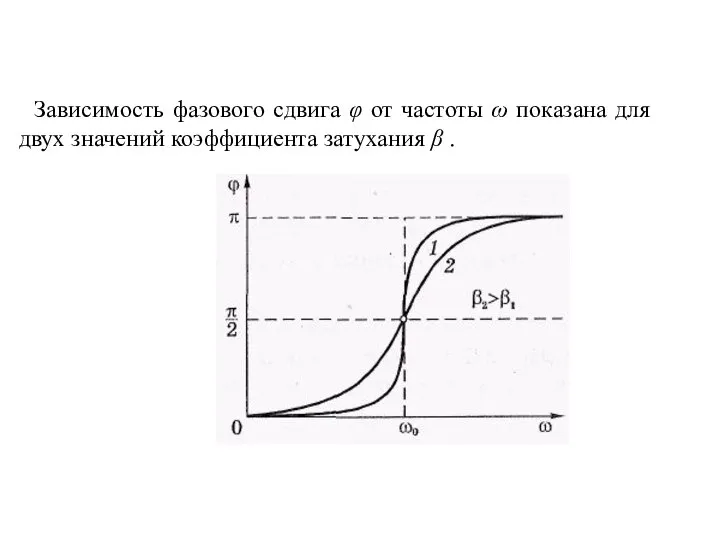
- 47. Зависимость фазового сдвига φ от частоты ω показана для двух значений коэффициента затухания β .
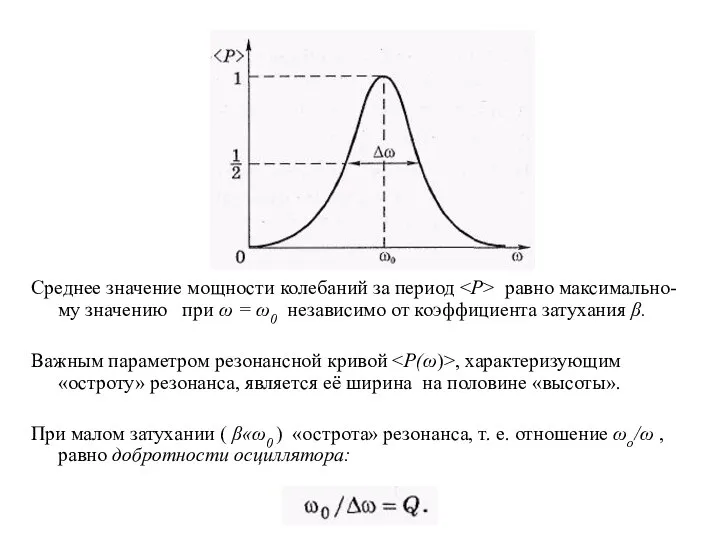
- 48. Среднее значение мощности колебаний за период равно максимально-му значению при ω = ω0 независимо от коэффициента
- 49. Энергия вынужденных колебаний. Так как Е = U+ К , то учтено, что
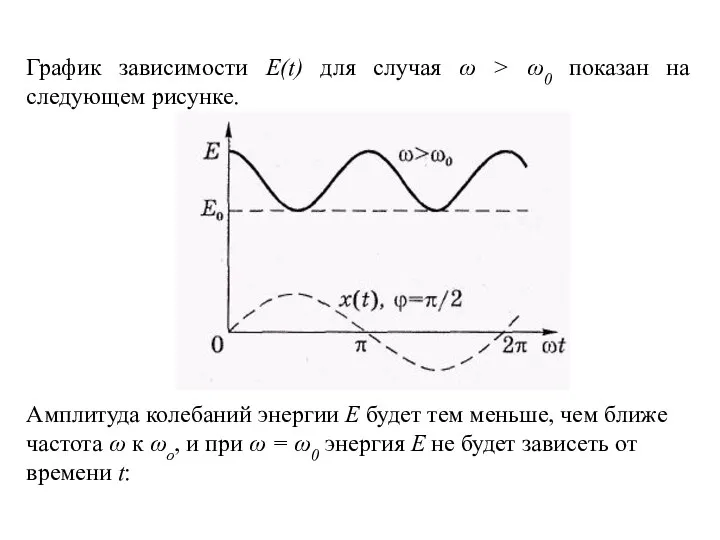
- 50. График зависимости E(t) для случая ω > ω0 показан на следующем рисунке. Амплитуда колебаний энергии Е
- 51. Зависимость полной энергии механической системы от времени , – диссипативная функция , − мощность внешнего источника
- 53. Скачать презентацию































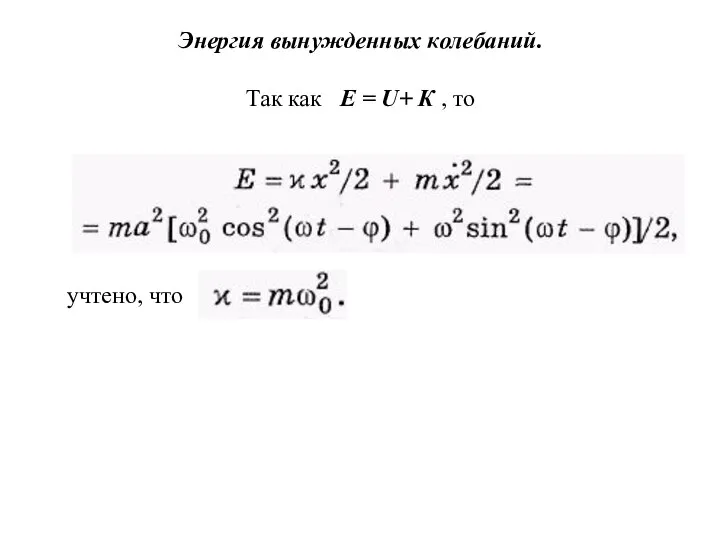

 Микропрод в стеклянной оболочке для тензометрии сосудов высокого давления
Микропрод в стеклянной оболочке для тензометрии сосудов высокого давления Муфты насоса
Муфты насоса Задачи на массовую долю элемента
Задачи на массовую долю элемента Применение фотоэффекта
Применение фотоэффекта Уравнение газа состояния идеального
Уравнение газа состояния идеального Инжекторный ДВС
Инжекторный ДВС Электрические цепи со взаимной индукцией
Электрические цепи со взаимной индукцией Өлшеудің белгісіздігі туралы түсінік
Өлшеудің белгісіздігі туралы түсінік Презентация на тему Виды излучений (11 класс)
Презентация на тему Виды излучений (11 класс)  Полупроводники
Полупроводники Занимательная физика. Задачи
Занимательная физика. Задачи Взаимодействие тел
Взаимодействие тел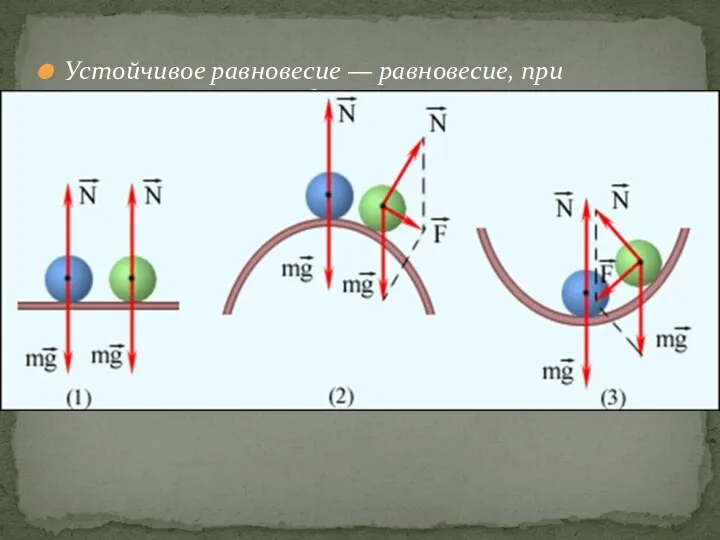 Устойчивое равновесие
Устойчивое равновесие Оптика
Оптика Высокая пластичность
Высокая пластичность Технология рентгеновских трубок. (Лекция 6)
Технология рентгеновских трубок. (Лекция 6) Зеркала
Зеркала Термодинамика и теплопередача. Реальные газы
Термодинамика и теплопередача. Реальные газы Законы Ньютона. Тест
Законы Ньютона. Тест ЯМР спектроскопия
ЯМР спектроскопия Презентация по физике "Понятия о механическом движении" -
Презентация по физике "Понятия о механическом движении" -  Решение задач. Электромагнитная индукция
Решение задач. Электромагнитная индукция Модели атомов. Атом водорода по теории Бора. Тема 7
Модели атомов. Атом водорода по теории Бора. Тема 7 Петля КМПЦ
Петля КМПЦ Зонная теория твёрдых тел
Зонная теория твёрдых тел Теплогазоснабжение с основами теплотехники. Лекция 1
Теплогазоснабжение с основами теплотехники. Лекция 1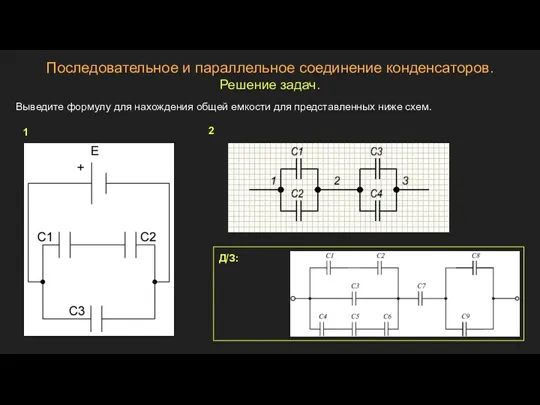 Последовательное и параллельное соединение конденсаторов. Решение задач
Последовательное и параллельное соединение конденсаторов. Решение задач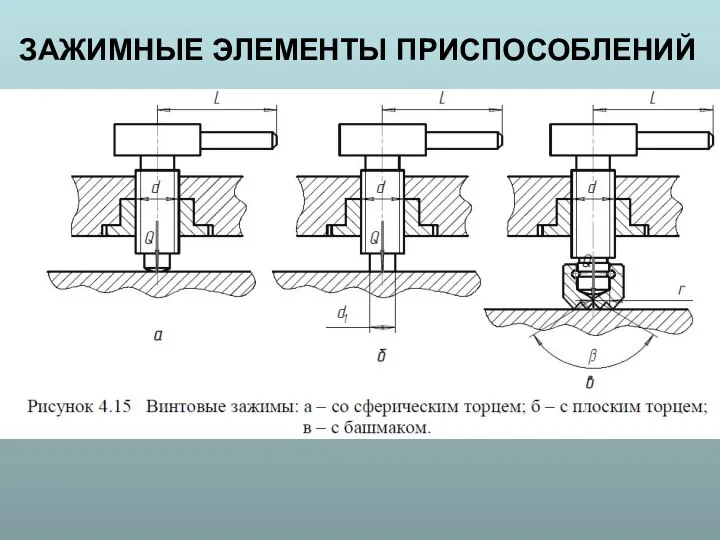 Зажимные элементы приспособлений
Зажимные элементы приспособлений