Якісна теорія динамічних систем. Моделювання динамічних систем Атрактори. Лекція 7

Лекція 7. Якісна теорія динамічних систем.
Моделювання динамічних систем
Регулярні атрактори.
Точка тяжіння ( N ≥ 1 ).
Граничний цикл ( N ≥ 2 ).
Перехідний процес
Періодичні коливання у лінійних системах із затуханням є вимушеними.
Регулярні атрактори є асимтотично стійкими та мають цілочисельну розмірність, що співпадає з метричною.

Лекція 7. Якісна теорія динамічних систем.
Моделювання динамічних систем
Нелінійні системи.
З фізичної точки зору зростання будь-якого параметра системи не може відбуватись до безмежності. Обмеженість енергетичних ресурсів рано чи пізно змусить це зростання зупинитись.
Нехай f(x) описує деяке збудження системи. Спочатку воно лінійно наростає, а потім швидко спадає до нуля. Якщо до збудження система була у стійкому рівноважному стані, то з часом вона до нього знову релаксує.
Якщо ж стартова точка системи є станом нестійкої рівноваги, то після збудження і слідуючого за ним повернення у початковий окіл рівноваги нестійкіть знову почне викидати траекторію за межі околу. Отож саме за рахунок нелінійності та нестійкості у системі реалізується режим періодичних коливань.
У системах з одним ступенем вільності (двовимірний ФП) в силу єдиності розв’язку коливальний режим може реалізовуватись виключно на граничному циклі.

Лекція 7. Якісна теорія динамічних систем.
Моделювання динамічних систем
Автоколивання.
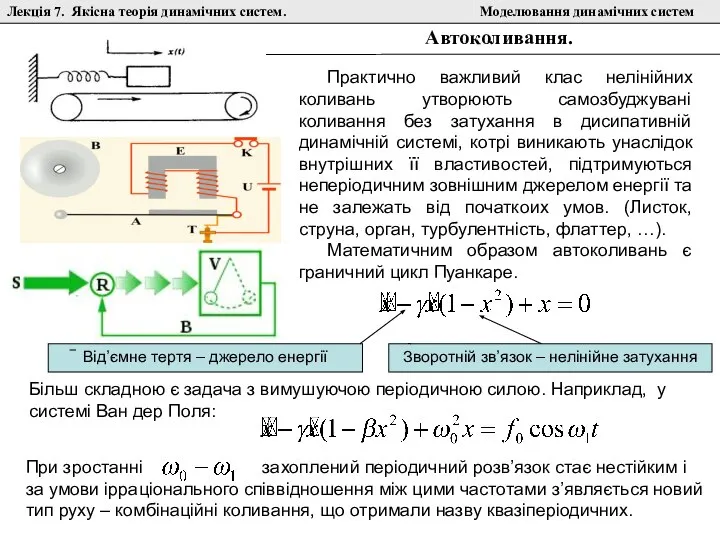
Практично важливий клас нелінійних коливань утворюють самозбуджувані коливання без затухання в дисипативній динамічній системі, котрі виникають унаслідок внутрішних її властивостей, підтримуються неперіодичним зовнішним джерелом енергії та не залежать від початкоих умов. (Листок, струна, орган, турбулентність, флаттер, …).
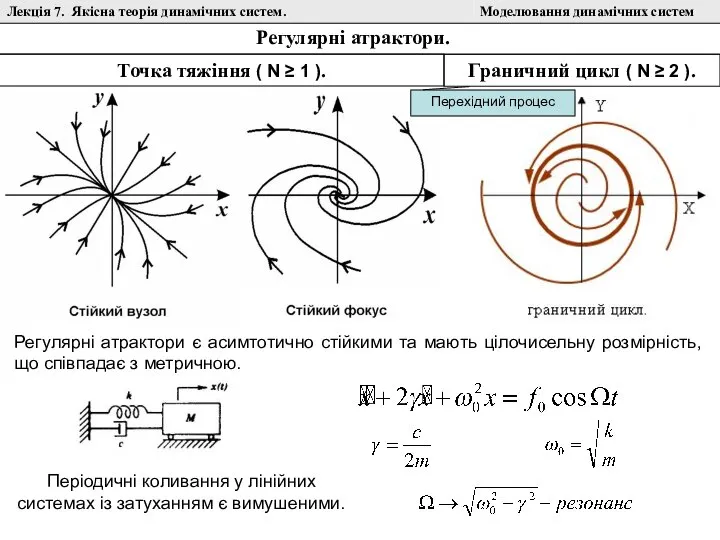
Математичним образом автоколивань є граничний цикл Пуанкаре.
Від’ємне тертя – джерело енергії
Зворотній зв’язок – нелінійне затухання
Більш складною є задача з вимушуючою періодичною силою. Наприклад, у системі Ван дер Поля:
При зростанні захоплений періодичний розв’язок стає нестійким і за умови ірраціонального співвідношення між цими частотами з’являється новий тип руху – комбінаційні коливання, що отримали назву квазіперіодичних.

Лекція 7. Якісна теорія динамічних систем.
Моделювання динамічних систем
хАос і ХаОс
Хаотична динаміка розвивається в рамках певної структури
Нелінійне диференціальне рівняння може мати обмежений неперіодичний розв’язок з хаотичною поведінкою навіть за умови, що рівняння не містить випадкових параметрів.
Випадкові рухи – умови і причини, що рух викликають є невідомими.
Хаотичні рухи – детеремінізовні задачі із заданими силами та параметрами.
Джерелом хаосу є сильна нелінійність

Лекція 7. Якісна теорія динамічних систем.
Моделювання динамічних систем
ДИВНІ (нерегулярні, хаотичні) атрактори ( N ≥ 3 ).
Перемішування.
Нестійкість експоненціально збільшує початкове збурення системи системи. У той же час через втрати енергії фазовий об’єм нелінійних дисипативних систем з часом прямує до нуля. Де компроміс ???
Фазовий об’єм в нелінійних дисипативних системах може збільшуватися в одних напрямках і одночасно зменшуватися в інших з превалюванням (у середньому) останніх.

Лекція 7. Якісна теорія динамічних систем.
Моделювання динамічних систем
σ = 10, β = 8/3, ρ > 1
Система Лоренца.
σ – число Прандтля,
ρ – параметр Релея,
β – описує геметрію системи.
Атрактор Лоренца
В силу теореми про єдиність розв’язку фазові траекторії перетинатись не можуть (що є головним інструментом доведення теореми Бендиксона-Пуанкаре про двохвимірний фазовий простір).

Лекція 7. Якісна теорія динамічних систем.
Моделювання динамічних систем
Дивний атрактор є математичним образом “ідеального” хаосу, який задовіль-няє певним математичним вимогам, але в реальних умовах практично не реалі-зується. У більшості практичних випадків реалізується режим квазігіперболічно-го атрактора (квазіатактора).
Система називається грубою, якщо мале збурення правої частини рівняння і варіації керуючих параметрів якісно не змінюють її фазовий портрет.
Система називається гіперболічною, якщо всі фазові траекторії є сідловими.
Можливі перетини стійкої та нестійкої сепаратрис сідлової точки на січенні Пуанкаре.

Лекція 7. Якісна теорія динамічних систем.
Моделювання динамічних систем
Фрактальна природа дивних атракторів
Динамічний хаос має фрактальну будову.

Лекція 7. Якісна теорія динамічних систем.
Моделювання динамічних систем
Порядок Шарковського
Яким показником оцінювати складність динамічної системи?
3 < 5 < 7 < 9 < ...
2*3 < 2*5 < 2*7 ...
22*3 < 22*5 < 22*7< …
23*3 < 23*5 < 23*7 ...
...
2n < 2n-1 ... < 2 < 1