Механика. Гравитационное поле. Лекция 6

I.Механика. Гравитационное поле.
На высоте h от поверхности Земли и для ускорения
свободного падения получим .
Движение спутников планет по круговым орбитам.
Запишем для этого движения второй закон Ньютона:
где m – масса спутника, M – масса планеты, R – ее радиус, h –высота орбиты над поверхностью планеты, - ускорение свободного падения на ее поверхности. Из этого уравнения можно найти скорость спутника и его период обращения Т.
Если , т.е. спутник летает на небольшой высоте, тогда
и для первой космической скорости получим:
.

I.Механика. Гравитационное поле.
- скорость, которую необходимо сообщить телу, чтобы оно стало спутником Земли (не вернулось на Землю).
Эллиптические орбиты.
В общем случае движение планет и их спутников происходит по эллиптическим орбитам. Гравитационные силы Солнца или планет не создают момента силы, поэтому момент импульса планет или спутников сохраняется и - радиус орбиты и скорость на орбите в перигее, а и - радиус и скорость в апогее (Рис.26).
Рис.26
Между ними существует следующее соотношение:

I.Механика. Гравитационное поле.
Потенциальная энергия гравитационного поля.
Рассмотрим гравитационное взаимодействие материальной точки массой m и шара (Земли) массой M и радиуса R (Рис.26).
Беря неопределенный интеграл, получим:
Рис.26
Если потенциальная энергия обращается в ноль на бесконечности, то константа интегрирования С=0 и
Если принять потенциальную энергию равной нулю на поверхности Земли и .
Потенциальная энергия в этом случае принимает вид:

I.Механика. Гравитационное поле.
Если высота над поверхностью шара (Земли) мала ,то
и
получаем известное выражение для потенциальной энергии тела на высоте h от поверхности Земли.
Вторая космическая скорость – скорость, которую необходимо сообщить телу, чтобы оно покинуло поле притяжение Земли (удалилось от него на бесконечность). Если принять потенциальную энергию на бесконечности, равной нулю, то закон сохранения энергии запишется в виде: , где выражение в
правой части равенства – полная энергия тела на поверхности Земли. На бесконечно большом расстоянии от Земли кинетическая и потенциальная энергии обращаются в ноль и

Расчет первой космической скорости у поверхности Земли

Вторая космическая скорость
VII= 11,2 км/с
Вторая космическая скорость – минимальная скорость, которую надо сообщить телу у поверхности Земли (или небесного тела) для того, чтобы оно преодолело гравитационное притяжение Земли (или небесного тела).

Третья космическая скорость
Минимальная скорость, которую надо сообщить телу у поверхности Земли для того, чтобы оно преодолело гравитационное притяжение Солнца.

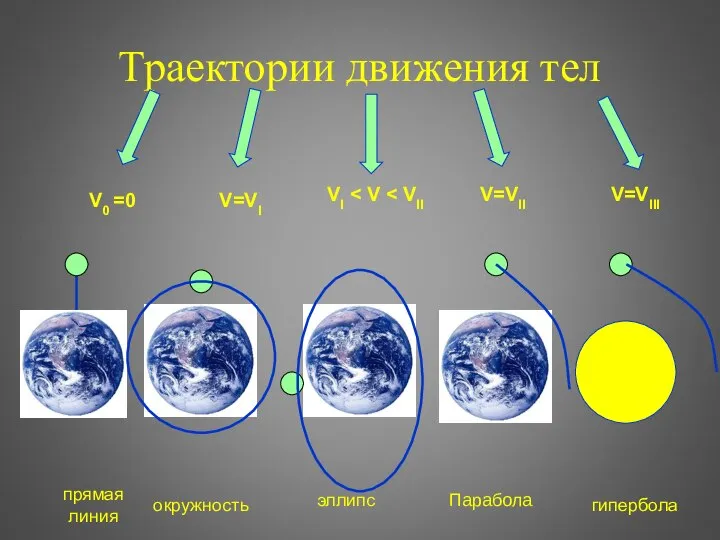
Траектории движения тел
V0 =0
V=VI
VI < V < VII
V=VII
V=VIII
прямая линия
окружность
эллипс
гипербола
Парабола

I.Механика. Метод Потенциальных кривых
отрицательна.
Слева от минимума тангенс угла наклона касательной отрицателен, а сила положительна. В точке минимума сила равна нулю, т.е. это есть положение равновесия. При смещении от этой точки вправо возникает сила возвращающая материальную точку в положение равновесия. Тот же результат будет и при смещении влево. Поэтому равновесие в этом случае является устойчивым. Вблизи максимума потенциального барьера положение равновесия неустойчиво. Пусть
– полная энергия материальной точки. Полная энергия
. В точках 3 и 4 пересечения прямой полной энергии с потенциальной кривой полная энергия равна потенциальной, поэтому движение на участке 3-4 возможно, а вне этого отрезка, где невозможно.

I.Механика. Метод Потенциальных кривых
отрицательна.
Слева от минимума тангенс угла наклона касательной отрицателен, а сила положительна. В точке минимума сила равна нулю, т.е. это есть положение равновесия. При смещении от этой точки вправо возникает сила возвращающая материальную точку в положение равновесия. Тот же результат будет и при смещении влево. Поэтому равновесие в этом случае является устойчивым. Вблизи максимума потенциального барьера положение равновесия неустойчиво. Пусть
– полная энергия материальной точки. Полная энергия
. В точках 3 и 4 пересечения прямой полной энергии с потенциальной кривой полная энергия равна потенциальной, поэтому движение на участке 3-4 возможно, а вне этого отрезка, где невозможно.

I.Механика. Гравитационное поле.
Примеры решения задач
Задача 31. Найдите путь, который пройдет тело за 1 с, свободно падая без начальной скорости на высоте от поверхности Земли, равной ее радиусу.
Решение. При свободном падении путь, проходимый телом
Равен где - ускорение свободного падения на высоте
и , откуда м.
Задача 32. Найдите силу притяжения к Земле космического корабля массы 10 тонн, находящегося на расстоянии от поверхности Земли, в четыре раза большем ее радиуса.
Решение. На расстоянии 5 радиусов Земли на космонавта будет действовать сила притяжения, равная
кН

I.Механика. Гравитационное поле.
Задача 33. Найдите отношение скоростей двух космических кораблей, вращающихся по круговым орбитам на расстояниях от поверхности Земли, равных одному и двум земным радиусам.
Решение. Запишем второй закон Ньютона, для спутников, вращающихся вокруг Земли на расстояниях одного и двух радиусов от поверхности под действием соответствующих сил тяжести:
Разделив первое уравнение на второе и извлекая квадратный корень получим 1,22.
Задача 34. Найдите период обращения спутника, движущегося по круговой орбите вблизи поверхности некоторой планеты, средняя плотность вещества которой равна 3,3 г/см3. Гравитационная постоянная 6,67·10–11 м3/кг·с2.

I.Механика. Гравитационное поле.
Решение. Запишем второй закон Ньютона для вращательного движение, выразив нормальное ускорение через период обращения:
.
Выразим в этом выражении массу планеты M через плотность и объем шара, тогда получим:
Задача 35. Спутник запущен вертикально вверх со второй космической скоростью. На некоторой высоте над поверхностью Земли потенциальная энергия спутника составляет 75% его первоначальной энергии. Потенциальная энергия на поверхности Земли при этом принимается нулевой. Найдите отношение этой высоты к радиусу Земли.

I.Механика. Гравитационное поле.
Решение. Запишем закон сохранения энергии, приняв, что потенциальная энергия обращается в ноль на поверхности Земли:
Задача 36. Спутник запускается со второй космической скорос-тью. Найдите, во сколько раз уменьшится его кинетическая энергия по сравнению с начальной на высоте, равной радиусу Земли. Участок разгона ракеты и сопротивление воздуха не учитывать.
Решение. Примем потенциальную энергию на поверхности Земли равной нулю, тогда на основе закона сохранения энергии:

I.Механика. Гравитационное поле.
Задача 37. Найдите расстояние, на которое ракета, запущенная вертикально вверх с поверхности Земли с первой космической скоростью , удалится от поверхности Земли. Радиус Земли равен
R = 6400 км. Вращение Земли не учитывать.
Решение. Принимая потенциальную энергию равной нулю на поверхности Земли, запишем закон сохранения энергии:
,
где – начальная кинетическая энергия ракеты, соответствующая
первой космической скорости , h –
высота подъема ракеты, на которой ее скорость обращается в ноль. Подставляя в первое уравнение, получим
,
откуда h=R=6400 км.