Молекулярная физика. Введение. Уравнение состояния. (Лекция 1)

Введение
Молекулярная физика и термодинамика
P
V
T
m
υ
n
Термодинамика — раздел физики, изучающий наиболее общие свойства макроскопических систем и способы передачи и превращения энергии в таких системах.
Описание процессов на микроуровне
Описание процессов на макроуровне
В статистических терминах:
средняя скорость, средняя длинна пробега, концентрация и т.д.
В интегральных терминах:
давление, объем, температура.
Молекулярная физика — раздел физики, который изучает физические свойства тел на основе рассмотрения их молекулярного строения.
Задачи молекулярной физики решаются методами статистической механики, термодинамики и физической кинетики, они связаны с изучением движения и взаимодействия частиц (атомов, молекул, ионов), составляющих физические тела.
Главное положение: любое тело (твердое, жидкое, газообразное) состоит из большего количества малых обособленных частиц – молекул.
Молекулы всякого вещества находятся в беспорядочном, хаотическом, не имеющем какого-либо преимущественного направления движении.
Доказательство хаотичности движения – броуновское движение.
Поведение системы состоящей из большего числа частиц не может быть описано методами классической механики и требует статистического подхода. Однако исторически методы описания таких систем формировались в отсутствии методов статистики и использовали интегральный подход.

Основные понятия термодинамики
Система — множество элементов, находящихся в отношениях и связях друг с другом, которое образует определённую целостность.
В каждый момент времени система может быть описана набором параметров (температура, объем, давление).
Состояние — совокупность устойчивых значений переменных параметров системы.
Если все параметры имеют одинаковое значение во всех частях системы, то такое состояние называется равновесным состоянием.
Соответственно, неравновесное состояние - состояние характеризующиеся неоднородным значением параметров (неоднородная температура, например.)
Последовательная смена состояний объекта называется процессом.
Переход системы из одного состояния в другое связан с нарушением равновесия системы. Т.е. переход системы между двумя равновесными состояниями осуществляется через последовательность неравновесных состояний, такой процесс называется неравновесным процессом.
Теоретически может быть описан только процесс состоящий из череды равновесных состояний – равновесный процесс.
Равновесным может быть только бесконечно медленный процесс – абстракция.
Все количественные выводы термодинамики строго применимы только к равновесным процессам и состояниям.
С течением времени, система предоставленная сама себе и находящаяся в неравновесном состоянии перейдет в равновесное состояние, которое будет устойчивым неопределенно долго, до тех пор, пока внешнее воздействие не приведет к изменениям.
1
2

Первое начало термодинамики
Внутренняя энергия (в термодинамике) – совокупность кинетической энергии элементов системы и потенциальной энергии взаимодействия между элементами системы. Энергия системы за вычетом кинетической энергии системы как целого и потенциальной энергии системы во внешнем поле сил.
Рассмотрим движущийся сосуд с газом. Внутренняя энергия складывается из кинетической энергии хаотического движения молекул, потенциальной энергии взаимодействия между молекулами и внутримолекулярной энергии. При этом кинетическая энергия связанная с движением сосуда и потенциальная энергия сосуда в поле сил тяжести не учитывается.
Работа
Тепло
1
1
2
3
Функция состояния — в термодинамике некая функция, зависящая от нескольких независимых параметров, которые однозначно определяют состояние термодинамической системы. Значение термодинамической функции состояния зависит только от состояния термодинамической системы и не зависит от того, как система пришла в это состояние.
Значение внутренней энергии однозначно определяется параметрами состояния системы (температура, объем, давление). В таком случае говорят, что величина является функцией состояния.
P
V
T
m
υ
n
Внутренняя энергия может изменяться за счет двух различных процессов: совершения над системой работы A и сообщения ей тепла Q.
Приращение внутренней энергии системы определяется суммой:
Здесь U12 – начальное и конечное значение внутренней энергии системы, A - работа совершаемая системой над внешними телами, A′ - работа внешних тел над системой. Соответствует закону сохранения энергии.
Такое энергетическое описание процесса называется первым началом термодинамики.
Первое начало термодинамики – количество тепла, сообщенное системе, идет на приращение внутренней энергии системы и на совершение системой работы над внешними телами.

Первое начало термодинамики
Обычно приходится разбивать рассматриваемый процесс на ряд элементарных процессов, каждый из которых соответствует малому изменению параметра. Для элементарного процесса можно записать:
Переходя к бесконечно малым.
Символ Δ′ (далее δ) - элементарное количество тепла или работы;
Δ (далее d) – элементарное приращение.
Элементарная величина может рассматриваться как приращение, если она соответствует переходу из одного состояние в другое, при том процесс не зависит от пути – величина является функцией состояния.
В отношении функции состояния можно говорить о «запасе». Может быть запас энергии, но не может быть запаса работы.
Внутренняя энергия – функция состояния, приращение обозначается Δ (далее d).
Работа, теплота – функции состояния, элементарное количество обозначается Δ′ (далее δ).
Корректная запись:
Некорректная запись:
(значило бы, что существует работа в начале пути и в конце пути)
Работа
Тепло
1
1
2
3

Температура
Если соприкасающиеся тела не обмениваются энергией путем теплообмена, то этим телам приписывается одинаковая температура.
Температура — физическая величина, характеризующая термодинамическую систему и количественно выражающая интуитивное понятие о различной степени нагретости тел.
Возьмем тело и приведем его в состояние теплового равновесия с тающим льдом, после этого припишем ему значение температуры T1=0. При этом отметим некоторый параметр тела, зависящий от нагрева, например, объем V0.
Приведем тело в контакт с кипящей водой. Припишем значение температуры T2=100, отметим соответствующее значение объема V100.
Если выбранный параметр изменяется линейно, то можно определить промежуточное значение температуры как:
Определенная таким образом температурная шкала называется шкалой Цельсия.
Физика сплошных сред рассматривает температуру как локальную макроскопическую переменную, т. е. величину, характеризующую мысленно выделяемую область (элементарный объём) сплошной среды, размеры которой бесконечно малы по сравнению с неоднородностями среды и бесконечно велики по отношению к размерам частиц (атомов, ионов, молекул и т. п.) этой среды.

Работа при изменении объема
Взаимодействие элементов системы можно характеризовать величиной давления.
Давление — физическая величина, численно равная силе, действующей на единицу площади поверхности перпендикулярно этой поверхности.
1
2
В случае движения поршня в цилиндре работа может быть выражена через давление и изменение объема.
Рассмотрим цилиндр с поршнем. Элементарная работа, совершаемая газом при перемещении поршня:
где f – сила, с которой газ действует на поршень. Через давление:
Выделим объем, тогда работа:
Если давление газа остается постоянным, работа, совершаемая при изменении объема:
Если же давление можно считать постоянным только ври бесконечно малом изменении объема, то работа определяется:
С учетом полученного выражения можно записать первое начало в виде:

Изопроцессы
Состояние некоторой массы газа определяется значением трех параметров: давления p, объема V и температуры T.
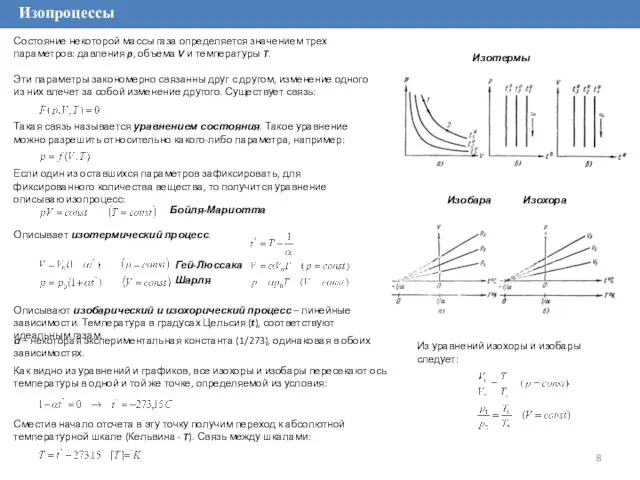
Эти параметры закономерно связанны друг с другом, изменение одного из них влечет за собой изменение другого. Существует связь:
Такая связь называется уравнением состояния. Такое уравнение можно разрешить относительно какого-либо параметра, например:
Если один из оставшихся параметров зафиксировать, для фиксированного количества вещества, то получится уравнение описываю изопроцесс:
Бойля-Мариотта
Гей-Люссака
Описывает изотермический процесс.
Описывают изобарический и изохорический процесс – линейные зависимости. Температура в градусах Цельсия (t), соответствуют идеальным газам.
Изотермы
Изобара Изохора
Шарля
α – некоторая экспериментальная константа (1/273), одинаковая в обоих зависимостях.
Как видно из уравнений и графиков, все изохоры и изобары пересекают ось температуры в одной и той же точке, определяемой из условия:
Сместив начало отсчета в эту точку получим переход к абсолютной температурной шкале (Кельвина - T). Связь между шкалами:
Из уравнений изохоры и изобары следует:

Уравнение состояния идеального газа
Объедения уравнения Бойля-Мариотта и Гей-Люссака, можно найти уравнение идеального газа. Рассмотрим процесс, на диаграмме P-V, перехода идеального газа из состояния 1 в состояние 2, через некоторое промежуточное состояние 1’.
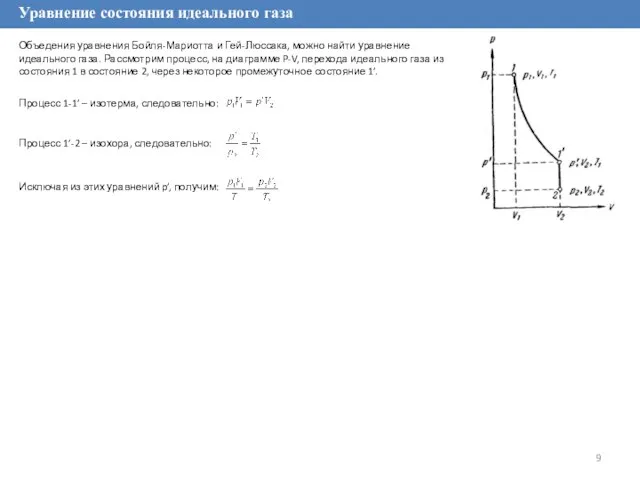
Процесс 1-1’ – изотерма, следовательно:
Процесс 1’-2 – изохора, следовательно:
Исключая из этих уравнений p’, получим:

Уравнение состояния идеального газа
Состояния 1 и 2 были взяты произвольным образом, все макропараметры изменились. Постоянным осталось только количество газа заключенного в сосуде.
Уравнение состояние идеального газа:
Закон Авогадро — в равных объёмах различных газов, взятых при одинаковых температурах и давлениях, содержится одно и то же количество молекул.
Авогадро установил, что килограмм-молекулы всех газов занимает при одинаковых условиях (T, P) одинаковый объем Vν.
При нормальных условиях: T= 0 C; P= 1 атм, этот объем составляет 22,4 м3/кмоль.
Можно заключить, что если рассматривать 1 килограмм-молекулы, то const в уравнение состояния будет одинаковой для всех газов. Обозначается буквой R.
R – универсальная газовая постоянная (физический смысл которой будет установлен далее) равная 8.31 [Дж/град∙моль].
От уравнения для одного моля можно перейти к уравнению для произвольного количества вещества используя массу 1 моля µ:
Моль - количество вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0,012 кг.
(приближенно) Моль - количество вещества содержащее 6∙1023 шт структурных элементов.

Основные выводы МКТ
Молекулярно-кинетическая теория (МКТ) — теория рассматривающая строение вещества (газов) с точки зрения трёх приближений:
- все тела состоят из частиц (молекул);
- частицы находятся в непрерывном хаотичном (тепловом) движении;
- частицы взаимодействуют друг с другом путём абсолютно упругих столкновений.
Оценим величину давления, оказываемого молекулами газа на стенку сосуда. Каждый элемент поверхности стенки ΔS за время Δt получает суммарный импульс ΔK, направленный по нормали к ΔS. Тогда из второго закона Ньютона:
Вычислим, на основе этих приближений, величину давления газа на стенки сосуда. Решение этой задачи дает выводы о физической природе абсолютной температуры.
Основными доказательствами положений МКТ стало объяснение явлений:
- диффузии;
- броуновского движения;
- изменение агрегатных состояний вещества.
Идеальный газ –совокупность одинаковых, хаотически движущихся, не взаимодействующих друг с другом на расстоянии молекул. Размеры молекул столь малы, что их суммарным объемом можно пренебречь по сравнению с объемом сосуда. Большую часть времени молекулы находятся в свободном движении, претерпевая иногда упругие соударения с другими молекулами или стенками сосуда.
Модель идеального газа применима к сильно разряженным реальным газам.
Введем ряд упрощений:
молекулы движутся только в трех взаимно перпендикулярных направлениях;
движение всех молекул можно характеризовать средней скоростью ˂υ˃.
В любой момент времени в выбранном направлении движется 1/6 всех молекул газа молекул.

Основные выводы МКТ
Вычислим импульс, сообщаемый стенку сосуда ударяющейся о нее молекулой. Так как после упругого удара импульс молекулы изменяет знак, то стенка, по третьему закону Ньютона получает двойной импульс:
За время до элемента стенки долетают все движущиеся по направлению к нему молекулы, заключенные в объеме цилиндра:
Число молекул, где n - концентрация:
Суммарный импульс:
По определению давления:
Выделим среднюю кинетическую энергию молекулы, соответствующую средней скорости:
- основное уравнение кинетической теории газов. Давление определяется средней кинетической энергии поступательного движения молекул.
Величина давления получена на основе микроскопических параметров газа: средняя скорость молекул и концентрация. Ранее была установлена связь давления с макроскопическими параметрами газа: объем и температура.
Умножим на объем моля газа:
Произведение числа молекул в единице объема на объем моля равно числу Авогадро, тогда можно записать:
Сопоставляя это уравнение с уравнением состояния идеального газа:
Средняя энергия зависит только от температуры и не зависит от массы молекул.