Постоянный_электрический_ток

Список литературы
Савельев И.В. Курс общей физики. В 5-и тт. Том 2. Электричество и магнетизм. ISBN - 978-5-8114-1208-2. Издательство «Лань». 2021 г.
Савельев И.В. Курс общей физики. В 5-и тт. Том 4. Волны. Оптика. ISBN - 978-5-8114-1210-5. Издательство «Лань». 2021 г.
Трофимова Т. И. Руководство к решению задач по физике : учебное пособие для прикладного бакалавриата: Учебное пособие/Трофимова Т. И..-М:Издательство Юрайт,2019, ISBN 978-5-9916-3429-8.-265. https://elis.psu.ru/node/557918

Проводники в электрическом поле
Лекция 5
Главы 3.1-4.3

Основные темы
Равновесие зарядов на проводнике
Проводник во внешнем электрическом поле
Электроемкость
Конденсаторы

Равновесие зарядов на проводнике
Носители зарядов в проводнике могут перемещаться под действием сколь угодно малой силы.
Для равновесия зарядов необходимо выполнение следующих условий:
Напряженность поля всюду внутри проводника должна быть равна 0
мы помним, что , это значит внутри проводника потенциал должен быть постоянным
(3.1)

Равновесие зарядов на проводнике
2. Напряженность поля на поверхности проводника должна быть в каждой точке направлена по нормали к поверхности
Следовательно, в случае равновесия зарядов поверхность проводника будет эквипотенциальной.
Если проводящему телу сообщить заряд q, то он распределится так, чтобы соблюдались условия равновесия.
Поскольку поле внутри проводника отсутствует, то и поток вектора электрического смещения через произвольную поверхность также равна 0
(3.2)

Равновесие зарядов на проводнике
Согласно теореме Гаусса и сумма зарядов внутри этой поверхности также будет равна 0.
Следовательно, при равновесии ни в каком месте внутри проводника не может быть избыточных зарядов
Все заряды распределяются по поверхности проводника с некоторой поверхностной плотностью σ.
Если из внутреннего объема проводника удалить часть вещества, то ничего не изменится.
То есть, на полом проводнике избыточный заряд распределяется так же, как и на сплошном

Равновесие зарядов на проводнике
Кроме того, одноименные элементарные заряды, образующие данный заряд q взаимно отталкиваются и стремятся расположиться на максимальном расстоянии друг от друга.
Представим небольшую цилиндрическую поверхность, образованную нормалями к поверхности проводника и основаниями dS, одно из которых расположено внутри, а другое вне проводника.
Поток вектора смещения через внутреннюю часть поверхности равен 0, так как E, а значит и D, внутри проводника равно 0.

Равновесие зарядов на проводнике
Вне проводника в непосредственной близости к нему напряженность поля E направлена по нормали к поверхности
Для выступающей наружу боковой поверхности цилиндра Dn=0, а для внешнего основания Dn=D.
Следовательно, поток смещения через рассматриваемую поверхность равен DdS, где D – смещение в непосредственной близости к поверхности.
Внутри цилиндра содержится сторонний заряд σdS, где σ - плотность заряда в данном месте поверхности проводника

Равновесие зарядов на проводнике
Применив теорему Гаусса, получим
Отсюда следует, что напряженность поля вблизи поверхности проводника равна
Где ε - диэлектрическая проницаемость среды, окружающей проводник
(3.3)

Равновесие зарядов на проводнике
На больших расстояниях от проводника эквипотенциальные поверхности имеют форму как у точечного заряда
По мере приближения к поверхности эквипотенциальные поверхности все больше повторяют поверхность проводника
Вблизи выступов эквипотенциальные поверхности располагаются гуще, значит и напряженность поле здесь больше.
Следовательно, плотность зарядов вблизи выступов особенно велика

Равновесие зарядов на проводнике
Вблизи углублений эквипотенциальные поверхности расположены реже, значит и напряженность поля и плотность зарядов ниже.
Вообще, плотность зарядов при заданном потенциале проводника определяется кривизной поверхности.
Она растет с увеличением положительной кривизны (выпуклости) и убывает с увеличением отрицательной кривизны (вогнутости).
Особенно велика плотность зарядов на остриях

Равновесие зарядов на проводнике
Напряженность поля вблизи остриев может быть настолько большой, что возникает ионизация молекул газа, окружающего проводник.
Ионы иного знака, чем q, притягиваются к проводнику и нейтрализуют заряд.
Ионы того же знака, что и q, отталкиваются от проводника, увлекая за собой молекулы газа.
В результате возникает ощутимое движение газа , называемое электрическим ветром.
Заряд проводника уменьшается, он как бы стекает с острия и уносится ветром. Такое явление называют истечением заряда с острия.

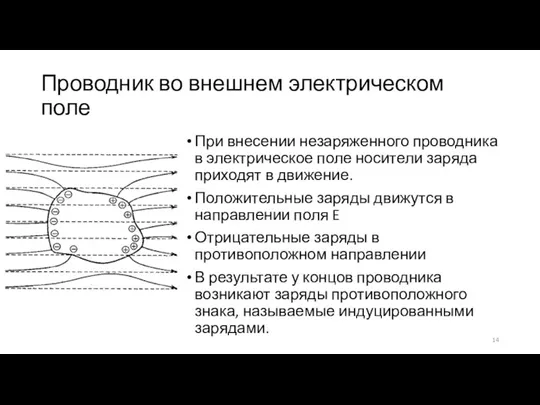
Проводник во внешнем электрическом поле
При внесении незаряженного проводника в электрическое поле носители заряда приходят в движение.
Положительные заряды движутся в направлении поля E
Отрицательные заряды в противоположном направлении
В результате у концов проводника возникают заряды противоположного знака, называемые индуцированными зарядами.

Проводник во внешнем электрическом поле
Поле этих зарядов направлено противоположно внешнему полю.
Накапливание зарядов у концов проводника приводит к ослаблению в нем поля.
Перераспределение зарядов происходит до тех пор, пока не начнут выполняться условия (3.1) и (3.2).
Нейтральный проводник разрывает часть линий напряженности. Они заканчиваются на отрицательных и начинаются на положительных зарядах.

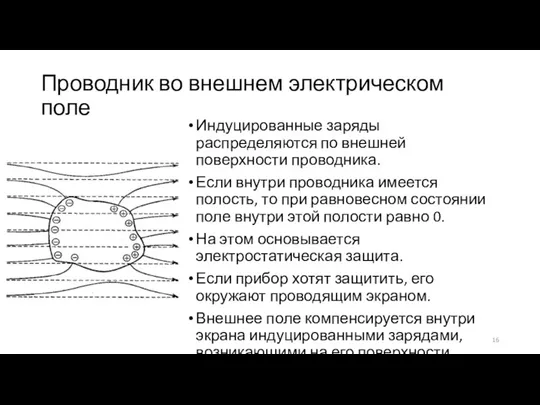
Проводник во внешнем электрическом поле
Индуцированные заряды распределяются по внешней поверхности проводника.
Если внутри проводника имеется полость, то при равновесном состоянии поле внутри этой полости равно 0.
На этом основывается электростатическая защита.
Если прибор хотят защитить, его окружают проводящим экраном.
Внешнее поле компенсируется внутри экрана индуцированными зарядами, возникающими на его поверхности.

Электроемкость
Сообщенный проводнику заряд q распределяется по его поверхности так, чтобы напряженность поля внутри проводника была равно нулю.
Если этому проводнику сообщить еще заряд такой же величины, то он распределится так же как и первый заряд.
В противном случае он создаст внутри проводника ненулевое поле.
Следовательно, потенциал уединенного проводника пропорционален находящемуся на нем заряду.
Действительно, увеличение заряда вызовет такое же увеличение напряженности электрического поля

Электроемкость
Так же точно увеличится и работа переноса единичного заряда из бесконечности на поверхность проводника, то есть потенциал проводника.
Таким образом, для уединенного проводника
Коэффициент пропорциональности С между потенциалом и зарядом называют электроемкостью проводника.
(3.4)
(3.5)

Электроемкость
Емкость численно равна заряду, сообщение которого проводнику повышает его потенциал на единицу
Потенциал заряженного шара радиуса R можно выразить как
Сопоставив (3.5) и (3.6) получим
(3.6)
(3.7)

Электроемкость
За единицу емкости принимают емкость такого проводника, потенциал которого изменяется на 1В при сообщении ему заряда 1Кл.
Эта единица называется фарадом (Ф).
Это шар, радиус которого в 1500 раз больше радиуса земли.

Конденсаторы
Уединенные проводники обладают небольшой емкостью.
Даже шар размером с планету Земля имеет емкость 700 мкФ
На практике требуются устройства, накапливающие заметные по величине заряды при небольшом размере
Такие устройства называются конденсаторами
В их основе лежит свойство увеличения электроемкости проводника по мере приближения к нему других тел
Под действием поля, создаваемого заряженным проводником, на поднесенном к нему теле возникают индуцированные или связанные заряды

Конденсаторы
Заряды, противоположные по знаку заряду проводника q, располагаются ближе к проводнику, чем одноименные, и следовательно оказывают большее влияние на потенциал.
При поднесении к заряженному проводнику какого-либо тела потенциал проводника уменьшается по абсолютной величине.
При том же заряде, это означает увеличение емкости проводника.
Конденсаторы делают в виде двух проводников, помещенных близко друг к другу.
Образующие конденсатор проводники называют его обкладками.

Конденсаторы
Обкладкам придают такую форму, чтобы поле концентрировалось между обкладками
Это могут быть две пластинки, два коаксиальных цилиндра или две концентрические сферы.
Соответственно бывают плоские, цилиндрические или сферические конденсаторы.
Основной характеристикой конденсатора является его емкость, которая прямо пропорциональна заряду и обратно пропорциональна разности потенциалов на его обкладках
(3.8)

Конденсаторы
Разность потенциалов ϕ1 - ϕ2 называют напряжением между соответствующими точками. Мы будем обозначать напряжение буквой U. В этом случае выражение (3.8) примет вид
Емкость определяется геометрией конденсатора и диэлектрическими свойствами среды, заполняющей пространство между обкладками.
(3.9)

Конденсаторы
Найдем формулу плоского конденсатора. Если площадь обкладки S, а заряд на ней q, то напряженность поля между обкладками
Разность потенциалов между обкладками
где S –площадь обкладки, d – зазор между обкладками, ε - диэлектрическая проницаемость вещества, заполняющего зазор
(3.10)
Отсюда, емкость плоского конденсатора

Конденсаторы
Из формулы (3.10) следует, что размерность ε0 измеряется в фарадах не метр Ф/м
Формула цилиндрического конденсатора
Где l – длина конденсатора, R1 и R2 – радиусы внутренней и внешней обкладок.
Емкость сферического конденсатора равна
(3.11)
(3.12)

Конденсаторы
Помимо емкости конденсатор характеризуется предельным напряжением Umax, которое можно прикладывать к обкладкам.
При превышении этого напряжения между обкладками проскакивает искра и конденсатор выходит из строя.

Постоянный электрический ток
Лекция 5
Главы 5.1-5.8

Основные темы
Электрический ток
Уравнение непрерывности
Закон Ома. Сопротивление проводников
Закон Ома для неоднородного участка цепи
Разветвленные цепи. Правило Кирхгофа
Мощность тока
Закон Джоуля-Ленца

Электрический ток
Если через некоторую воображаемую поверхность переносится суммарный заряд, отличный от нуля, говорят что через эту поверхность течет электрический ток.
Ток может течь в твердых телах (металлы, полупроводники), в жидкостях (электролиты) и в газах.
Для протекания тока необходимо наличие в данном теле (или в данной среде) заряженных частиц, которые могу свободно перемещаться.
Такие частицы называют носителями тока.
Ими могут быть электроны, ионы, либо макрочастицы (пылинки и капельки воды)

Электрический ток
Ток возникает при условии, что внутри тела существует электрическое поле.
Носители заряда принимают участие в молекулярном тепловом движении с некоторой скоростью v даже в отсутствие поля.
В этом случае через произвольную площадку проходит в среднем одинаковое количество носителей любого знака в обе стороны
При включении поля на хаотичное движение носителей со скоростью v накладывается упорядоченное движение со скоростью u.

Электрический ток
Таким образом, скорость носителей будет v + u.
Так как среднее значение v равно нулю, то средняя скорость носителей равна
То есть, электрический ток можно определить как упорядоченное движение электрических зарядов.
Количественной характеристикой тока служит величина заряда, переносимого через рассматриваемую поверхность в единицу времени
(5.1)

Электрический ток
Электрический ток может быть обусловлен движением как положительных, так и отрицательных носителей.
Перенос отрицательного заряда в одном направлении эквивалентен переносу положительного заряда в другом.
Если ток создается носителями обоих знаков, за время dt через данную поверхность положительные носители переносят dq+ в одном направлении и отрицательные – заряд dq- в другом, то
За направление тока принимается направление движения положительных носителей

Электрический ток
Электрический ток может быть распределен по поверхности, через которую он течет, неравномерно.
Ток можно охарактеризовать с помощью вектора плотности тока j.
Этот вектор численно равен силе тока dI через расположенную в данной точке перпендикулярную к направлению движения носителей площадку dS⊥ , отнесенной к величине этой площадки.
За направление j принимается направление вектора скорости u+ упорядоченного движения положительных носителей
(5.2)

Электрический ток
Зная вектор плотности тока в каждой точке пространства, можно найти силу тока I через любую поверхность S
Из (5.3) следует, что сила тока есть поток вектора плотности тока через поверхность
Пусть в единице объема содержится n+ положительных носителей и n- отрицательных.
Алгебраическая величина зарядов носителей равно e+ и e-.
(5.3)

Электрический ток
Если под действием поля носители приобретают средние скорости u+ и u-, то за единицу времени через единичную площадку пройдет n+u+ положительных носителей, которые перенесут заряд e+n+u+.
Аналогично отрицательные носители перенесут e-n-u-
Таким образом, для плотности тока получается
В векторном виде
(5.4)
(5.5)

Электрический ток
Вектор u- направлен противоположно вектору j. При умножении его на отрицательный скаляр e- получается вектор одинакового направления с j.
Произведение e+n+ дает плотность заряда положительных носителей ρ+, аналогично e-n- дает плотность заряда отрицательных носителей ρ-. Тогда выражение (5.5) можно записать в виде
Ток, не изменяющийся со временем, называется постоянным.
(5.6)

Электрический ток
Для постоянного тока справедливо соотношение
Где q – заряд, переносимый через рассматриваемую поверхность за конечное время t.
В СИ единица силы тока Ампер (А). Единица заряда кулон определяется как заряд, переносимый за 1 с через поперечное сечение проводника при силе тока в 1А.
(5.7)
(5.8)

Электродвижущая сила
Если в проводнике создать электрическое поле и не принять мер для его поддержания, то перемещение носителей очень быстро приведет к тому, что поле внутри проводника исчезнет и ток прекратится.
Для того чтобы поддерживать ток, нужно от конца с меньшим потенциалом непрерывно отводить приносимые током заряды, к концу с большим потенциалом непрерывно их подводить.
То есть необходимо обеспечить круговорот зарядов, чтобы они двигались по замкнутому пути.

Электродвижущая сила
В замкнутой цепи наряду с участками, на которых положительные носители движутся в сторону убывания потенциала ϕ, должны быть участки, на которых перенос положительных зарядов происходит в направлении возрастания потенциала ϕ.
Перемещение носителей на этих участках возможно лишь с помощью сил не электростатического характера.
Такие силы называют сторонними силами.

Электродвижущая сила
Таким образом, для поддержания тока необходимы сторонние силы, действующие на всем протяжении цепи или на отдельных ее участках.
Сторонние силы можно охарактеризовать работой, которую они совершают над перемещающимися по цепи зарядами.
Величина, равная работе сторонних сил над единичным положительным зарядом, называется электродвижущей силой (ЭДС), действующей в цепи или на ее участке.
(5.9)

Электродвижущая сила
Размерность ЭДС совпадает с размерностью потенциала.
ЭДС измеряется в тех же единицах, что и потенциал (Вольты).
Стороннюю силу Fст, действующую на заряд q, можно представить в виде
Векторную величину E* называют напряженностью поля сторонних сил.
Работа сторонних сил на участке цепи 1-2 равна
(5.10)

Электродвижущая сила
Разделив эту работу на заряд q, получим ЭДС, действующую на данном участке
Аналогичный интеграл, вычисленный для замкнутой цепи, даст ЭДС, действующую в этой цепи.
Таким образом, ЭДС, действующая в замкнутой цепи, может быть определена как циркуляция вектора напряженности сторонних сил.
(5.11)
(5.12)

Электродвижущая сила
Кроме сторонних сил на заряд действуют силы электростатического поля FE=qE.
Следовательно результирующая сила, действующая в каждой точке цепи на заряд q, равна
Работа, совершаемая этой силой над зарядом q на участке цепи 1-2, определяется выражением
(5.13)

Электродвижущая сила
Величина, численно равная работе, совершаемой электростатическими и сторонними силами при перемещении единичного положительного заряда, называется падением напряжения или просто напряжением U на данном участке цепи.
Участок цепи, на котором не действуют сторонние силы, называется однородным.
Участок, на котором на носители тока действуют сторонние силы, называется неоднородным.
Для однородного участка цепи напряжение это разность потенциалов
(5.14)
(5.15)

Закон Ома. Сопротивление проводников.
Немецкий физик Ом экспериментально установил, что сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения U на проводнике
Обозначенная буквой R величина называется электрическим сопротивлением проводника.
Единицей сопротивления служит Ом, равный сопротивлению такого проводника, в котором при напряжении 1В течет ток силой в 1А.
(5.16)

Закон Ома. Сопротивление проводников.
Величина сопротивления зависит от формы и размеров проводника, а также свойств материала, из которого он сделан.
Для однородного цилиндрического проводника
Где l - длина проводника, S – площадь его поперечного сечения, ρ - зависящий от свойств материал коэффициент, называемый удельным электрическим сопротивлением вещества.
В системе СИ удельное сопротивление ρ измеряется в ом-метрах (Ом*м).
(5.17)

Закон Ома. Сопротивление проводников.
Пусть носители заряда перемещаются по вектору j, напряжение поля соответствует вектору E.
В изотропном проводнике упорядоченное движение носителей тока происходит в направлении вектора E, поэтому направление векторов j и E совпадают.
Выделим мысленно в окрестности некоторой точки элементарный цилиндрический объем с образующими, параллельно векторам j и E.

Закон Ома. Сопротивление проводников.
Через поперечное сечение цилиндра течет ток силой jdS.
Напряжение, приложенное к цилиндру, равно Edl.
Сопротивление цилиндра ρ(dl/dS). Тогда
Поскольку направление векторов j и E совпадают, можно записать
(5.18)

Закон Ома. Сопротивление проводников.
Величина σ называется удельной электрической проводимостью материала.
Единица, обратная Ому является Сименс
Единицей удельной проводимости является Сименс на метр (См/м).
Проводимость или сопротивление зависят от сил взаимодействия носителей тока с частицами, из которых состоит вещество проводника.
Чем больше эти силы взаимодействия, тем больше сопротивление.

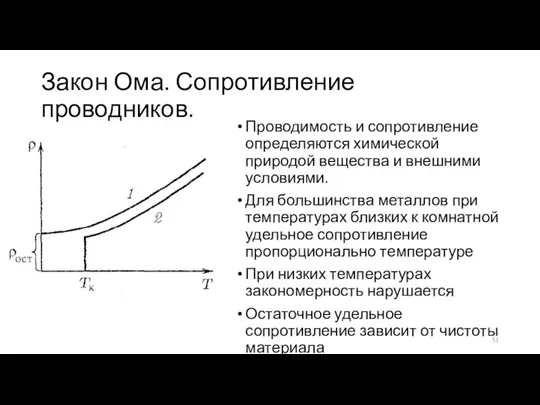
Закон Ома. Сопротивление проводников.
Проводимость и сопротивление определяются химической природой вещества и внешними условиями.
Для большинства металлов при температурах близких к комнатной удельное сопротивление пропорционально температуре
При низких температурах закономерность нарушается
Остаточное удельное сопротивление зависит от чистоты материала

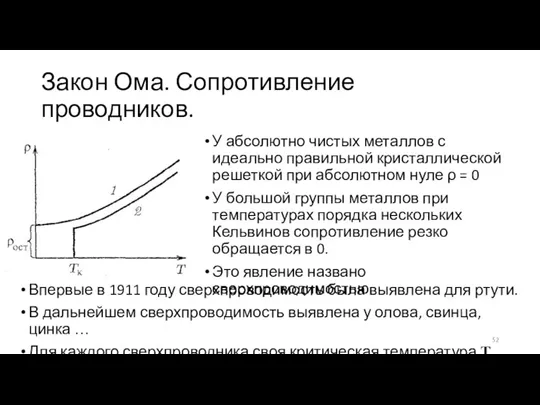
Закон Ома. Сопротивление проводников.
У абсолютно чистых металлов с идеально правильной кристаллической решеткой при абсолютном нуле ρ = 0
У большой группы металлов при температурах порядка нескольких Кельвинов сопротивление резко обращается в 0.
Это явление названо сверхпроводимостью.
Впервые в 1911 году сверхпроводимость была выявлена для ртути.
В дальнейшем сверхпроводимость выявлена у олова, свинца, цинка …
Для каждого сверхпроводника своя критическая температура Tk

Закон Ома. Сопротивление проводников.
Состояние сверхпроводимости может быть разрушено под воздействием магнитного поля.
Зависимость сопротивления от температуры используется в термометрах сопротивления.
Обычно это платиновая проволочка, намотанная на фарфоровый каркас.
Проградуирован по постоянным температурным точкам.
Позволяет измерять температуру с погрешностью в несколько сотых Кельвина.

Закон Ома для неоднородного участка цепи
На неоднородном участке цепи на носители тока дейcтвуют кроме электростатических сил eE, сторонние силы eE*
Сторонние силы способны вызывать упорядоченное движение носителей в той же мере, что и электростатические
Средняя скорость упорядоченного движения носителей в проводнике пропорциональна электростатической силе eE.
При наличии сторонних сил средняя скорость движения носителей будет пропорциональна суммарной силе eE+ eE*
Значит плотность тока в этих точках пропорциональна сумме напряженностей E + E*

Закон Ома для неоднородного участка цепи
Выражение (5.19) это более общий случай по сравнению с (5.18).
Допустим, что внутри неоднородного участка цепи существует линия (контур тока), удовлетворяющая условиям:
В каждом сечении, перпендикулярном контуру, величины j, σ, E, E* имеют с достаточной точностью одинаковые значения
Векторы j, E и E* в каждой точке направлены по касательной к контуру
Поперечное сечение проводника может быть непостоянным
(5.19)

Закон Ома для неоднородного участка цепи
Выберем произвольное направление движения по контуру от конца 1 к концу 2 участка цепи.
Спроецируем векторы (5.19) на элемент контура dl, в результате получим
(5.20)
Проекция каждого из векторов равна модулю вектора, взятому со знаком + или – в зависимости от направления вектора по отношению к dl. То есть jl=j или jl= -j

Закон Ома для неоднородного участка цепи
Вследствие сохранения заряда сила постоянного тока в каждом сечении должна быть одинаковой.
Поэтому величина I=jlS постоянна вдоль контура
Силу тока в данном случае можно рассматривать как алгебраическую величину. Тогда
Умножим это соотношение на dl и проинтегрируем вдоль контура

Закон Ома для неоднородного участка цепи
Выражение ρdl/S представляет собой сопротивление участка контура длины dl, а интеграл от этого выражения – сопротивление R участка цепи.
Первый интеграл в правой части дает ϕ1 - ϕ2, а второй – ЭДС 12 , действующую на участке цепи. Таким образом получаем
ЭДС – величина алгебраическая. Если ЭДС способствует движению положительных носителей в направлении 1-2, ЭДС > 0, а если препятствует, тогда ЭДС < 0.
(5.21)

Закон Ома для неоднородного участка цепи
Эта формула выражает закон Ома для неоднородного участка цепи.
Положив ϕ1 = ϕ2, получим выражение закона Ома для замкнутой цепи
Здесь - ЭДС, действующая в цепи, R – суммарное сопротивление всей цепи.
(5.21)
(5.22)

Разветвленные цепи. Правило Кирхгофа.
Для расчета разветвленных цепей пользуются правилами Кирхгофа
Узлом называется точка, в которой сходится более чем два проводника
Считается что ток, текущий к узлу имеет один знак, а от узла - другой
Первое правило - Алгебраическая сумма токов, сходящихся в узле равна нулю
(5.23)

Разветвленные цепи. Правило Кирхгофа.
Это правило вытекает из закона сохранения заряда.
Для постоянного тока ∇j всюду равна нулю. Следовательно, поток вектора j (т.е. алгебраическая сумма токов, текущих через окружающую узел воображаемую замкнутую поверхность) должен быть равен нулю.
Второе правило относится к любому выделенному в разветвленной цепи замкнутому контуру (1-2-3-4-1)

Разветвленные цепи. Правило Кирхгофа.
Зададим направление обхода (например по часовой стрелке)
Применим к каждому из неразветвленных участков закон Ома
При сложении этих выражений потенциалы взаимно уничтожаются и получается уравнение (5.24)

Разветвленные цепи. Правило Кирхгофа.
Уравнение (5.24) выражает второе правило Кирхгофа
Это уравнение можно составить для всех замкнутых контуров
Однако независимыми будут уравнения тех контуров, которые нельзя получить наложением других контуров один на другой.
Для данной цепи можно составить три уравнения
(5.24)
1 – для контура 1-2-3-6-1, 2- для контура 3-4-5-6-3,
3 – для контура 1-2-3-4-5-6-1

Разветвленные цепи. Правило Кирхгофа.
Последний контур получается наложением первых двух, поэтому уравнения не будут независимыми.
В качестве независимых можно взять любые два уравнения из трех.
При составлении уравнений второго правила Кирхгофа токам и ЭДС нужно приписывать знаки в соответствии с выбранным направлением обхода.
Ток I1 и его нужно считать отрицательным, так как он течет навстречу направлению обхода
ЭДС также нужно считать отрицательной, так как она действует против направления обхода

Разветвленные цепи. Правило Кирхгофа.
Направления обхода в каждом из контуров можно выбирать произвольно и независимо от направлений в других контурах
При этом может быть, что один и тот же ток или ЭДС войдут в разные уравнения с разными знаками
Следует помнить что через любое сечение неразветвленного участка цепи течет один и тот же ток
Например от точки 6 до источника тока 2 течет такой же ток как от источника 2 до точки 3

Разветвленные цепи. Правило Кирхгофа.
Число независимых уравнений, составленных в соответствии с первым и вторым правилами Кирхгофа, оказывается равным числу различных токов, текущих в разветвленной цепи.
Поэтому, если заданы ЭДС и сопротивления для всех неразветвленных участков, то могут быть вычислены все токи.
Можно найти ЭДС, которые нужно включить в каждый из участков цепи, что получить при заданных сопротивлениях нужные токи.

Мощность тока
Рассмотрим произвольный участок цепи постоянного тока, к концам которого приложено напряжение U
За время t через каждое сечение проводника проходит заряд q=It
Это равносильно тому, что заряд It переносится за время t из одного конца проводника в другой
При этом силы электростатического поля и сторонние силы, действующие на данном участке, совершают работу
(5.25)

Мощность тока
Разделив работу A на время t, за которое она совершается, получим мощность, развиваемую током на данном участке
Эта мощность может расходоваться на нагрев, на протекание химических реакций, на перемещение внешних тел и т.д.
Отношение мощности ΔP, развиваемой током в объеме проводника ΔV, к этому объему называется удельной мощностью тока Руд, отвечающей данной точке проводника.
Удельная мощность есть мощность, развиваемая в единице объема проводника.
(5.26)
(5.27)

Закон Джоуля-Ленца
Если проводник неподвижен и химических реакций в нем не протекает, работа тока затрачивается на увеличение внутренней энергии проводника, в результате чего проводник нагревается.
Принято говорить, что при протекании тока в проводнике выделяется теплота
Выразив U через RI, получим формулу
Это соотношение было установлено экспериментально Джоулем и Ленцем независимо и названо законом Джоуля-Ленца
(5.28)

Закон Джоуля-Ленца
Если сила тока изменяется во времени, то количество теплоты, выделяющееся за время t, вычисляется по формуле
От вычисления выделяемой теплоты во всем проводнике можно перейти к выражению, характеризующих выделение теплоты в различных местах проводника
Для этого выделим в проводнике элементарный объем в виде цилиндра.
(5.29)