Режимы движения жидкости. Лекция 3

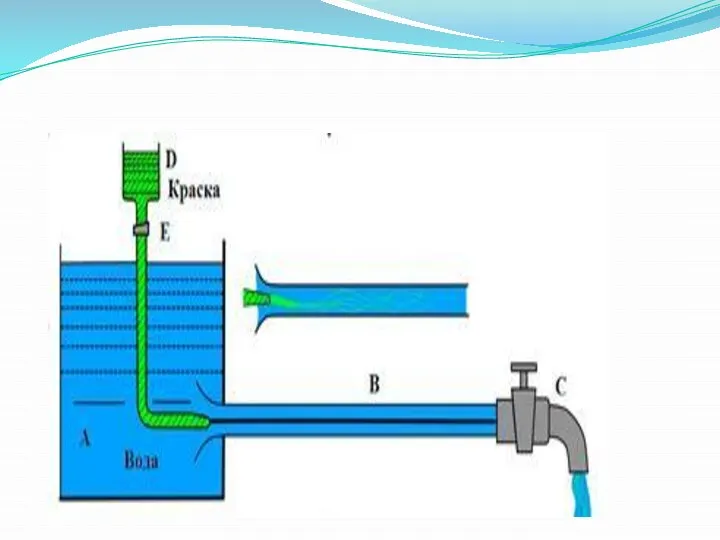
При наблюдении за движением жидкости в трубах и каналах, можно
заметить, что в одном случае жидкость сохраняет определенный строй
своих частиц, а в других – перемещаются бессистемно.

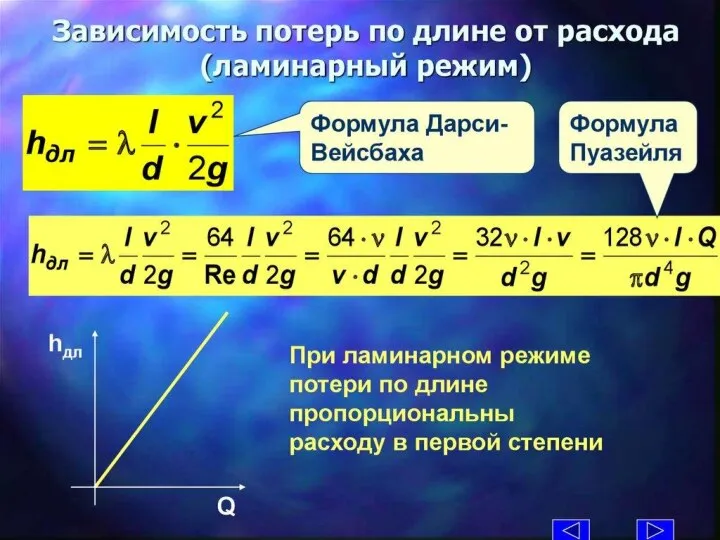
Потери напора на трение( по длине) при ламинарном движении.

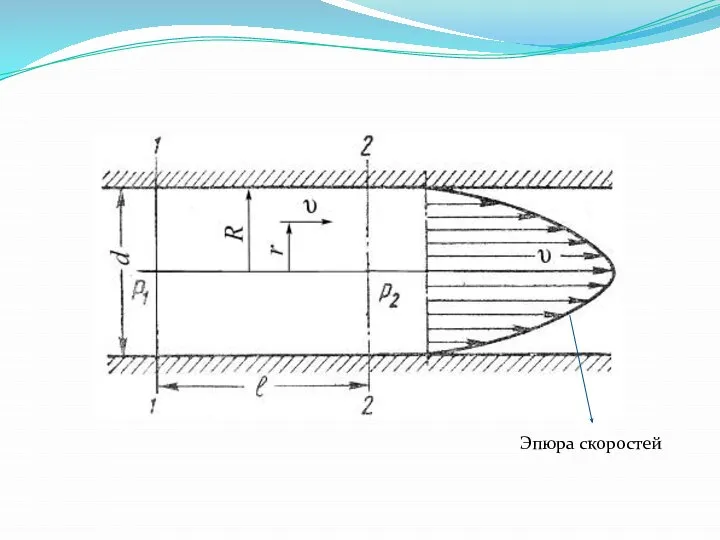
Как показывают исследования, при ламинарном течении жидкости в круглой трубе максимальная скорость находится на оси трубы. У стенок трубы скорость равна нулю, т.к. частицы жидкости покрывают внутреннюю поверхность трубопровода тонким неподвижным слоем. От стенок трубы к ее оси скорости нарастаю плавно. График распределения
скоростей по поперечному сечению потока представляет собой параболоид вращения, а сечение параболоида осевой плоскостью – квадратичную параболу

Эпюра скоростей

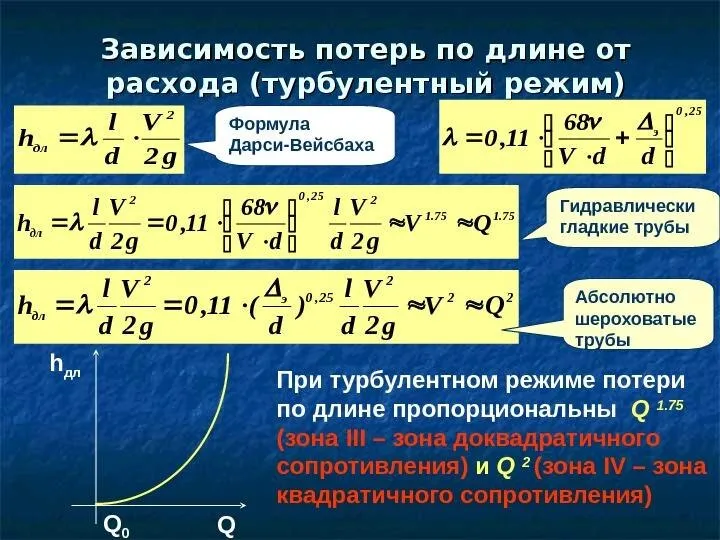
Потери напора при турбулентном течении жидкости

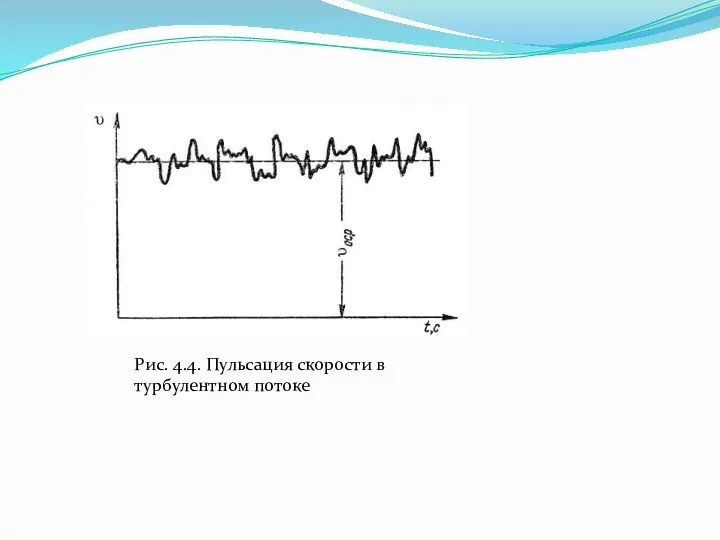
Для турбулентного течения характерно перемешивание жидкости, пульсации скоростей и давлений. Если с помощью особо чувствительного прибора-самописца измерять пульсации, например, скорости по времени в фиксированной точке потока, то получим картину, подобную показанной на рис.4.4. Скорость беспорядочно колеблется около некоторого осредненного по времен значения υоср, которое данном случае остается постоянным. Характер линий тока в трубе в данный момент времени отличается большим разнообразием (рис.4.5). Рис. 4.4. Пульсация скорости в турбулентном потоке

Рис. 4.4. Пульсация скорости в
турбулентном потоке

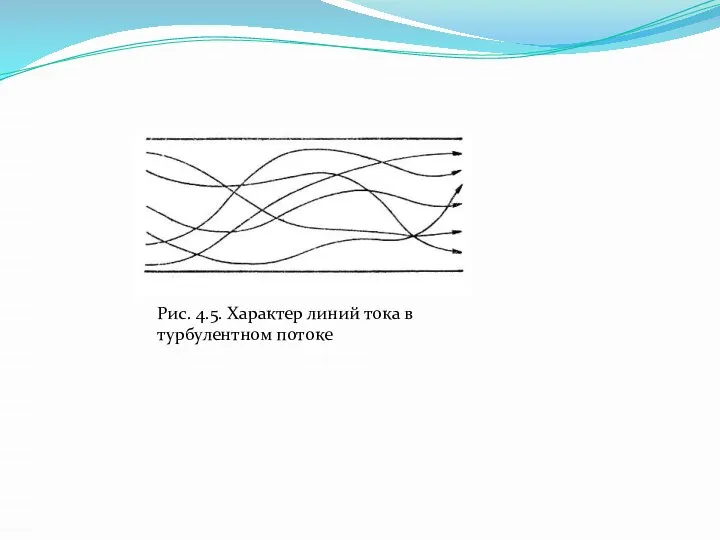
Рис. 4.5. Характер линий тока в
турбулентном потоке

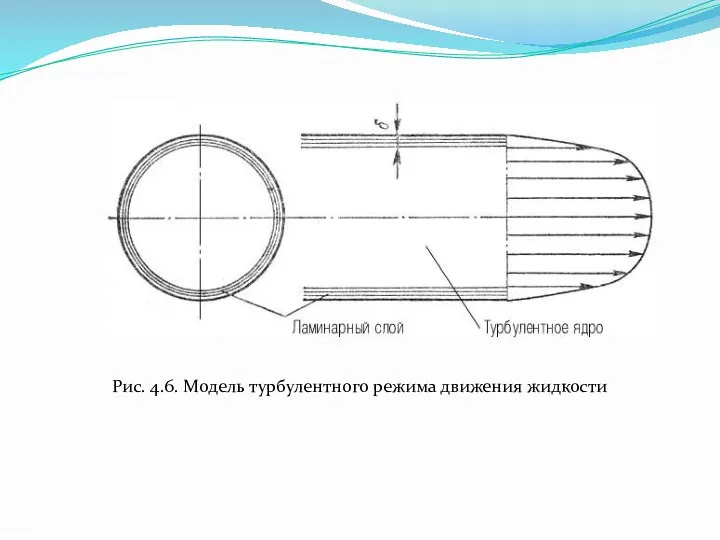
При турбулентном режиме движения жидкости в трубах эпюра распределения скоростей имеет вид, показанный на рис. 4.6. В тонком пристенном слое толщиной δ жидкость течет в ламинарном режиме, а остальные слои текут в турбулентном режиме, и называются турбулентным ядром. Таким образом, строго говоря, турбулентного движения в чистом виде не существует. Оно сопровождается ламинарным движением у стенок, хотя слой δ с ламинарным режимом весьма мал по сравнению с турбулентным ядром.

Рис. 4.6. Модель турбулентного режима движения жидкости

Основной расчетной формулой для потерь напора при турбулентном течении жидкости в круглых трубах является уже приводившаяся выше эмпирическая формула , называемая формулой Вейсбаха-Дарси и
имеющая следующий вид:
Различие заключается лишь в значениях коэффициента гидравлического трения λ. Этот коэффициент зависит от числа Рейнольдса
Re и от безразмерного геометрического фактора – относительной Шероховатости ∆/d (или ∆/r0, где r0 – радиус трубы).

Задача 2.
Q=2000 л/мин.
D=200 мм.
L= 20 м.
∆= 0.2 мм.
ν = 0,01 см^2/ c.
γ= 8000 Н/м^3
Pl-?
Hl-?
Задача 1.
Q=1000 л/мин.
D=100 мм.
L= 5 км.
∆= 0.2 мм.
ν = 0,013 см^2/ c.
γ= 8000 Н/м^3
Pl-?
Hl-?

Местные потери. Формула Вейсбаха
V – средняя скорость потока перед препятствием.
Иначе - обязательно оговаривается.
ξ (кси) (иногда ζ (дзета)) - коэффициент местного сопротивления, зависит от его вида, размера и конструктивного выполнения.

Определение коэффициентов местных сопротивлений
Коэффициент ξ в основном берется из справочной литературы, кроме случаев:
внезапное расширение потока;
внезапное сужение;
диффузор и конфузор (плавное расширение/сужение);
резкий и плавный поворот русла (колено/отвод).
Во всех случаях - только для турбулентного режима течения.

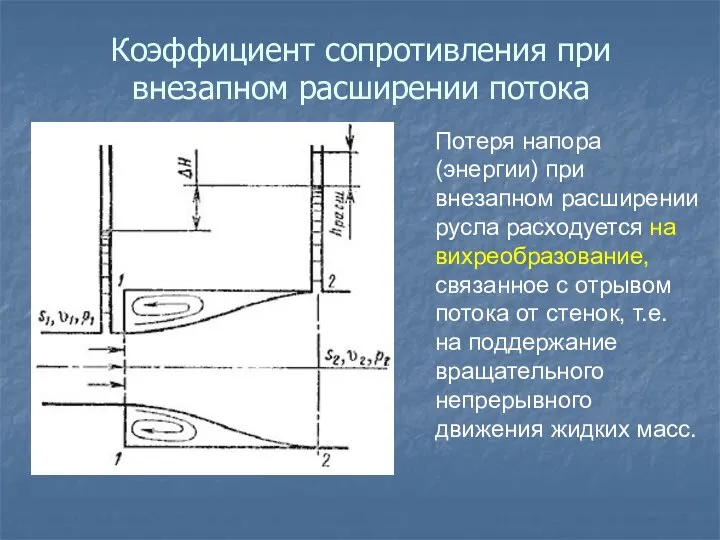
Коэффициент сопротивления при внезапном расширении потока
Потеря напора (энергии) при внезапном расширении русла расходуется на вихреобразование, связанное с отрывом потока от стенок, т.е. на поддержание вращательного непрерывного движения жидких масс.

Рассмотрим два сечения потока: 1-1 и 2-2 .
Допущения:
а) поток турбулентный (α = 1);
б) напряжения трения τ = 0.
Уравнение Бернулли для сечений 1-1 и 2-2:
Из теоремы об изменении количества движения
Учитывая, что
и разделив на
,

получаем:
или
, то есть
- теорема Борда (1766)
Теорема Борда - потеря напора при внезапном расширении русла равна скоростному напору, определенному по разности скоростей

Частный случай:
при (расширение из трубы в бассейн)
- полная потеря напора
Из уравнения неразрывности
и

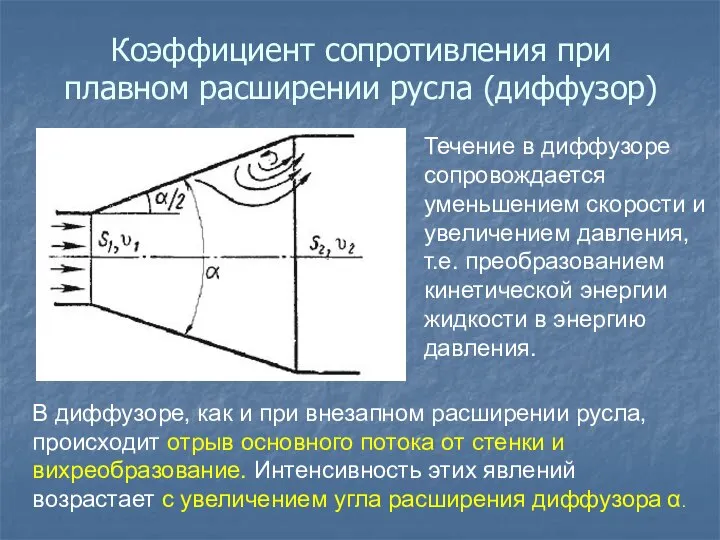
Коэффициент сопротивления при плавном расширении русла (диффузор)
Течение в диффузоре сопровождается уменьшением скорости и увеличением давления, т.е. преобразованием кинетической энергии жидкости в энергию давления.
В диффузоре, как и при внезапном расширении русла, происходит отрыв основного потока от стенки и вихреобразование. Интенсивность этих явлений возрастает с увеличением угла расширения диффузора α.

Кроме того, в диффузоре имеются и обычные потери на трение, подобные тем, которые возникают в трубах постоянного сечения.
Полную потерю напора в диффузоре рассматривают как сумму двух слагаемых:
hтр и hрасш - потери напора на трение и расширение (вихреобразование).
Без вывода:
где n = S2/S1 = ( r2/r1 ) 2 - степень расширения диффузора;
k - коэффициент смягчения (отн. уступа). При α = 5…20° k = sin α.

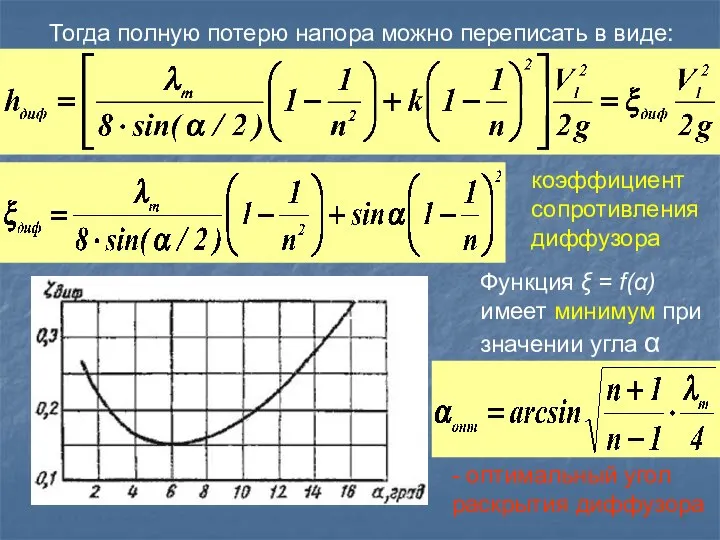
Тогда полную потерю напора можно переписать в виде:
коэффициент сопротивления диффузора
Функция ξ = f(α) имеет минимум при значении угла α
- оптимальный угол раскрытия диффузора

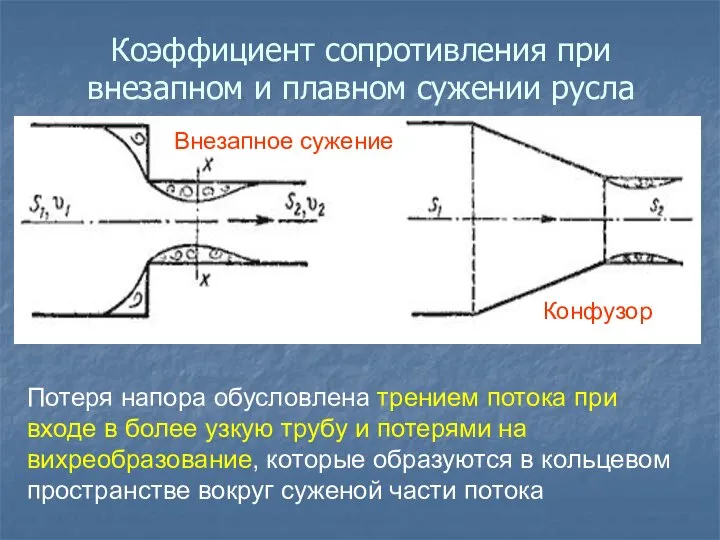
Коэффициент сопротивления при внезапном и плавном сужении русла
Потеря напора обусловлена трением потока при входе в более узкую трубу и потерями на вихреобразование, которые образуются в кольцевом пространстве вокруг суженой части потока
Конфузор
Внезапное сужение

Полная потеря напора определится по формуле:
Коэффициент сопротивления сужения ξсуж определяется по полуэмпирической формуле И.Е. Идельчика:
где
n = S1/S2
При выходе трубы из резервуара больших размеров (когда можно считать, что S2/S1 = 0), а также при отсутствии закругления входного угла, коэффициент сопротивления ξсуж = 0,5.

Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления. В конфузоре имеются лишь потери на трение
где коэффициент сопротивления конфузора определяется по формуле
где n = S1/S2 - степень сужения
Внимание! При сужении русла потери напора относятся к скорости за препятствием V2 !

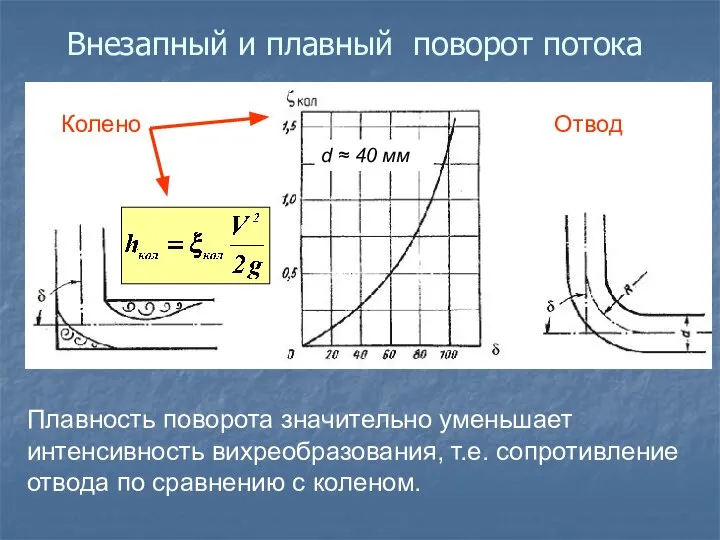
Внезапный и плавный поворот потока
Плавность поворота значительно уменьшает интенсивность вихреобразования, т.е. сопротивление отвода по сравнению с коленом.
Колено
Отвод
d ≈ 40 мм

Коэффициент сопротивления отвода ξотв зависит от отношения R / d, угла δ, и формы поперечного сечения трубы. Для отводов круглого сечения с углом δ= 90° и R/d > 1 при турбулентном течении можно воспользоваться эмпирической формулой:
Для углов δ ≤ 70° коэффициент сопротивления
При δ > 100°

Справочные коэффициенты местных потерь