Содержание
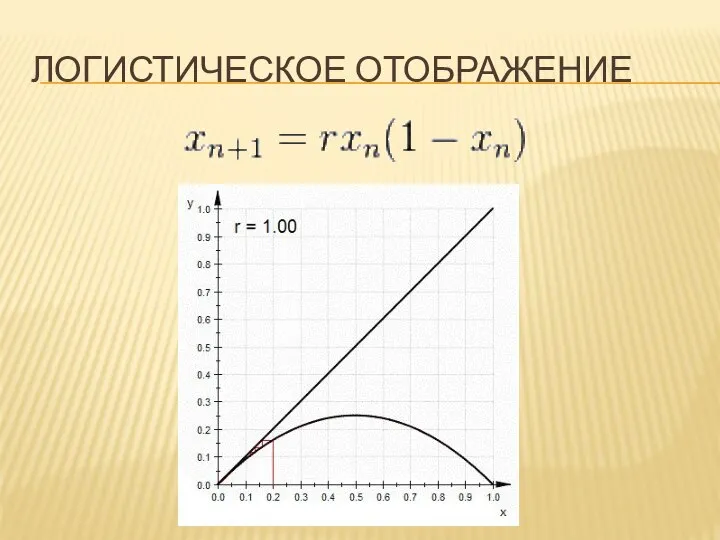
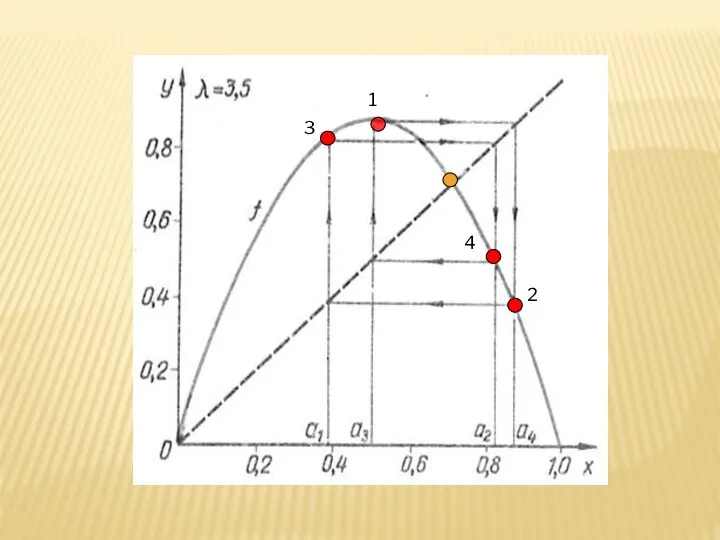
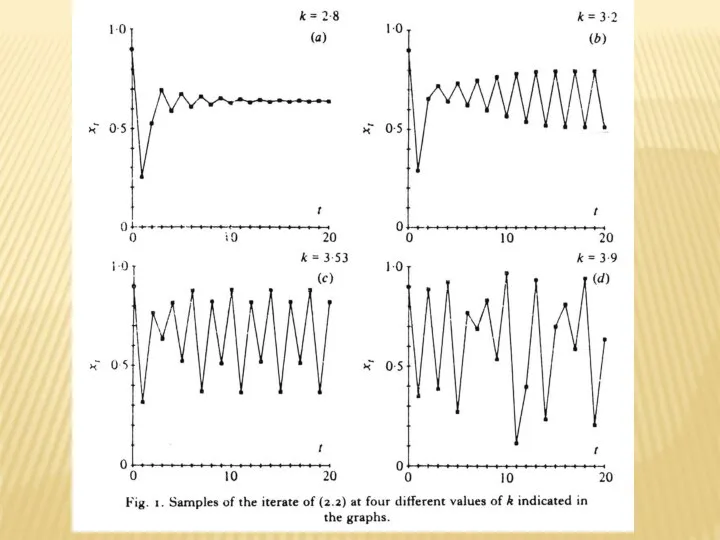
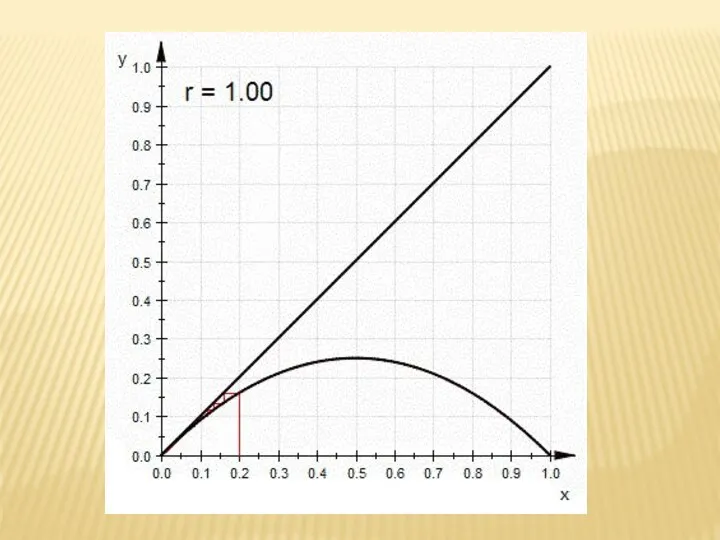
- 2. ЛОГИСТИЧЕСКОЕ ОТОБРАЖЕНИЕ
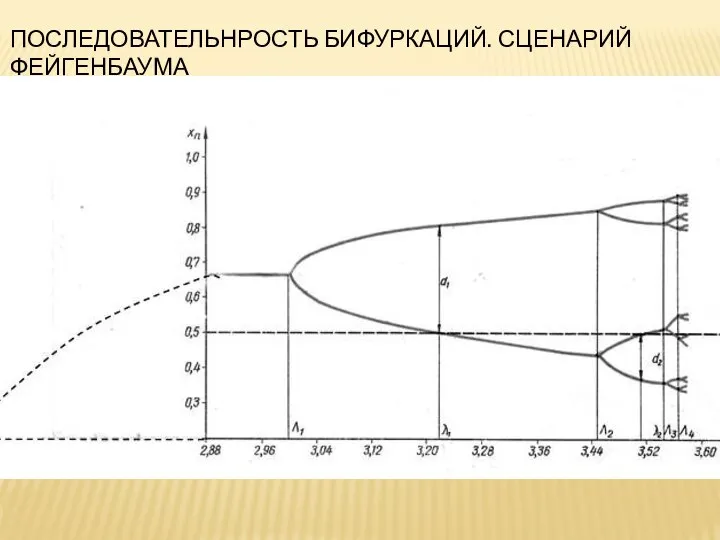
- 9. ПОСЛЕДОВАТЕЛЬНРОСТЬ БИФУРКАЦИЙ. СЦЕНАРИЙ ФЕЙГЕНБАУМА
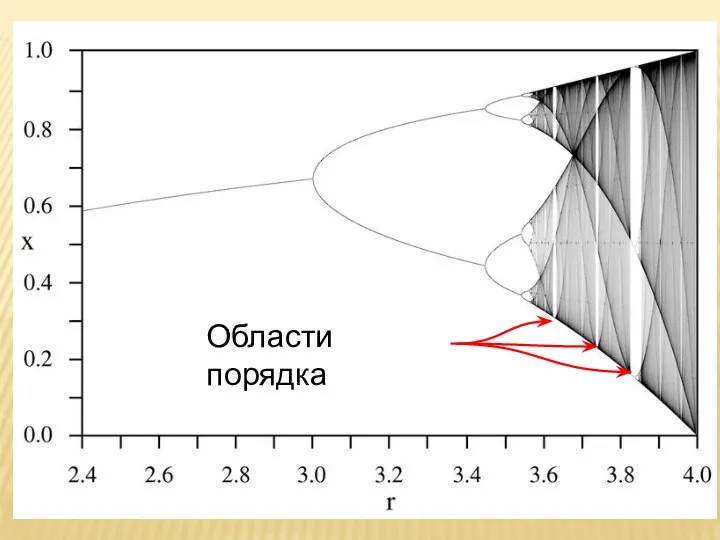
- 10. Области порядка
- 14. ВОЗВРАЩЕНИЕ ПУАНКАРЕ хаос Область порядка порядок
- 15. СЛУЧАЙНЫЕ ПРОЦЕССЫ ШУМЫ
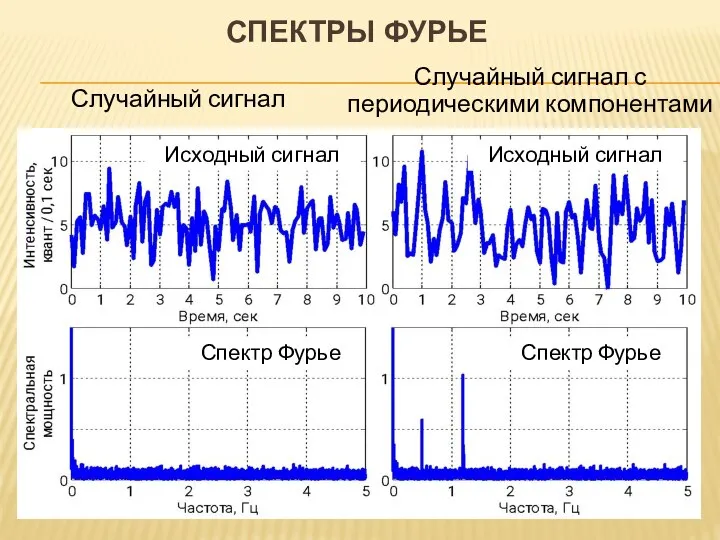
- 16. Случайный сигнал Случайный сигнал с периодическими компонентами СПЕКТРЫ ФУРЬЕ
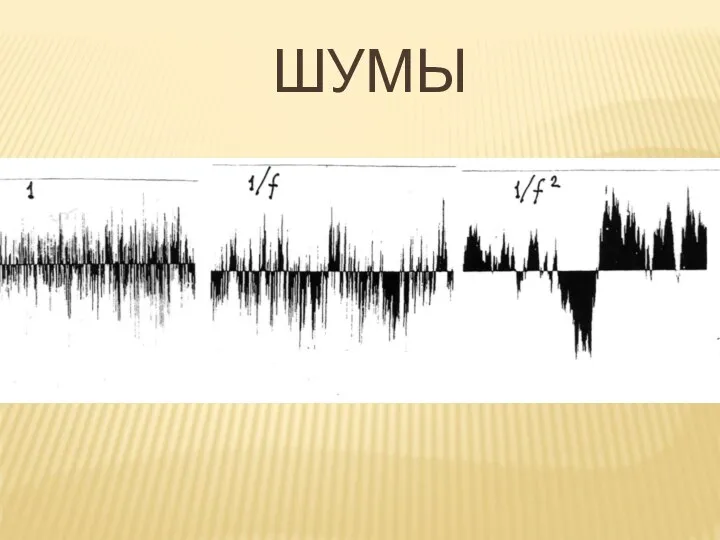
- 17. ШУМЫ
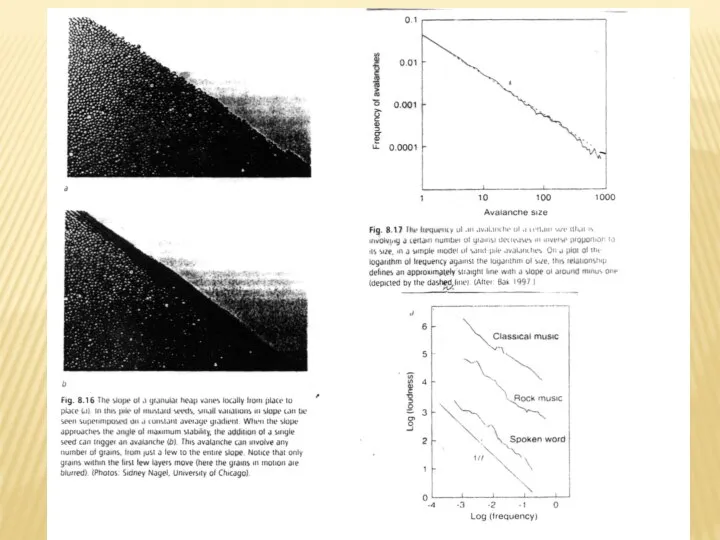
- 19. СТЕПЕННЫЕ РАСПРЕДЕЛЕНИЯ В ПРИРОДЕ
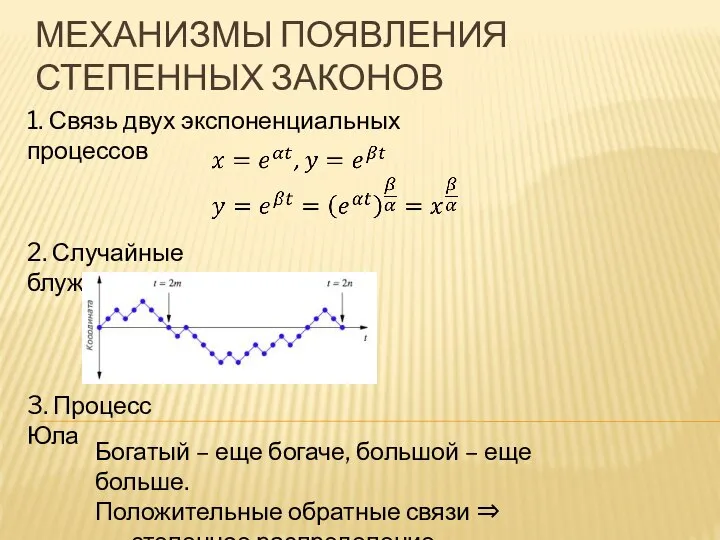
- 20. МЕХАНИЗМЫ ПОЯВЛЕНИЯ СТЕПЕННЫХ ЗАКОНОВ 1. Связь двух экспоненциальных процессов 2. Случайные блуждания 3. Процесс Юла Богатый
- 21. МЕХАНИЗМЫ ПОЯВЛЕНИЯ СТЕПЕННЫХ ЗАКОНОВ 4. Пороговые явления в перколяции. Решетка размера N×N. Вероятность окрашивания клетки –
- 22. МЕХАНИЗМЫ ПОЯВЛЕНИЯ СТЕПЕННЫХ ЗАКОНОВ 5. Самоорганизующаяся критичность. Рост деревьев VS. пожары. Самоподдержание вблизи критической точки.
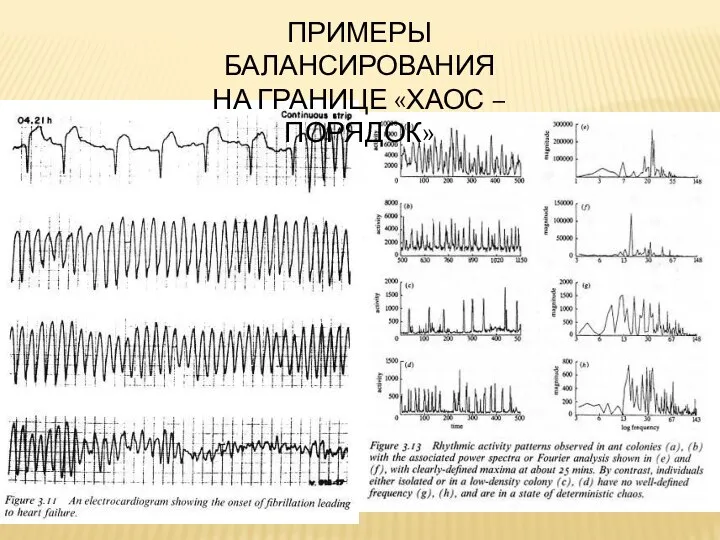
- 23. ПРИМЕРЫ БАЛАНСИРОВАНИЯ НА ГРАНИЦЕ «ХАОС – ПОРЯДОК»
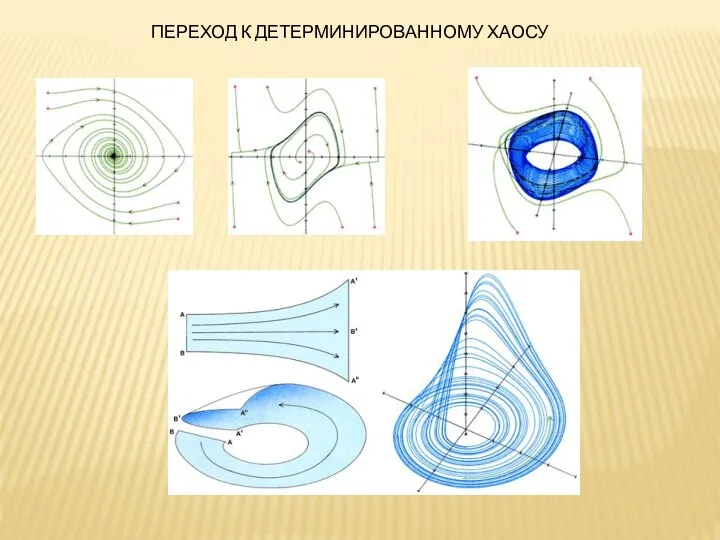
- 24. ПЕРЕХОД К ДЕТЕРМИНИРОВАННОМУ ХАОСУ
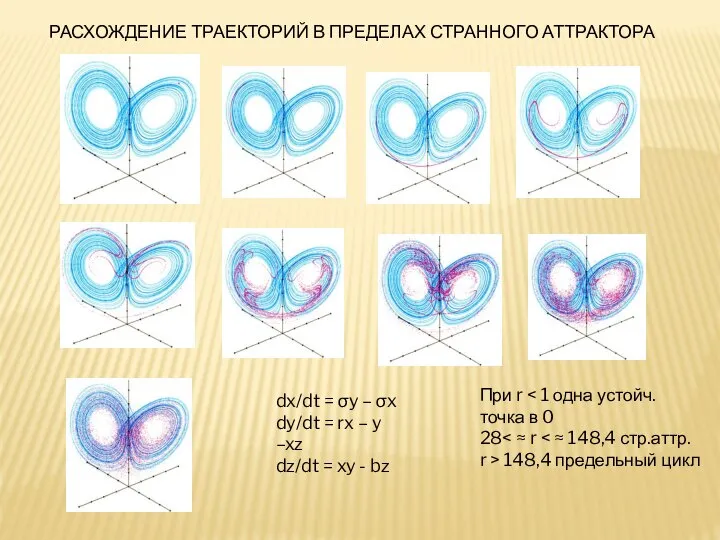
- 25. РАСХОЖДЕНИЕ ТРАЕКТОРИЙ В ПРЕДЕЛАХ СТРАННОГО АТТРАКТОРА dx/dt = σy – σx dy/dt = rx – y
- 29. АВТОКОРРЕЛЯЦИИ ПРИ МЕХАНОЭМИССИИ КРОВИ
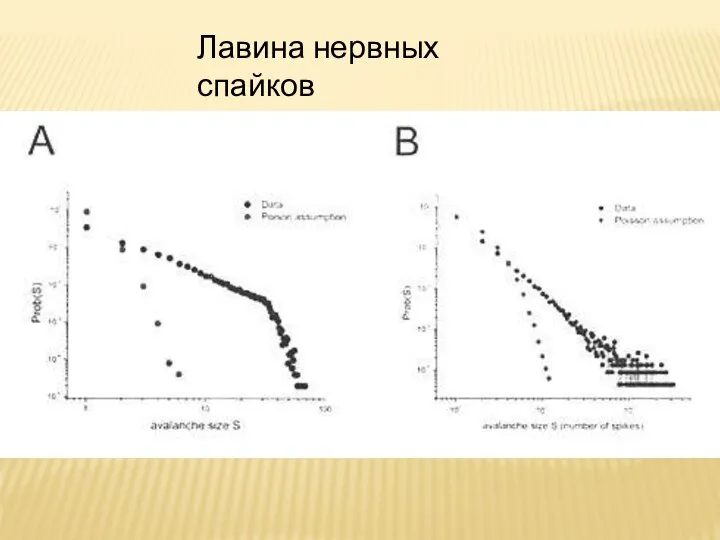
- 30. Лавина нервных спайков
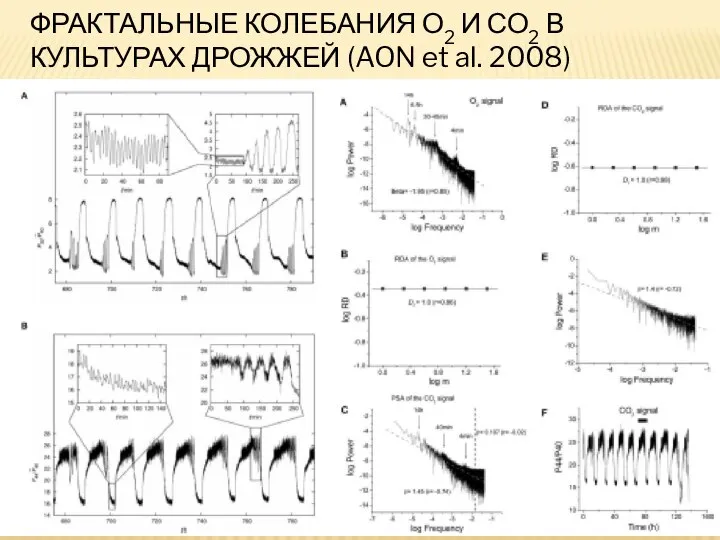
- 31. ФРАКТАЛЬНЫЕ КОЛЕБАНИЯ О2 И СО2 В КУЛЬТУРАХ ДРОЖЖЕЙ (AON et al. 2008)
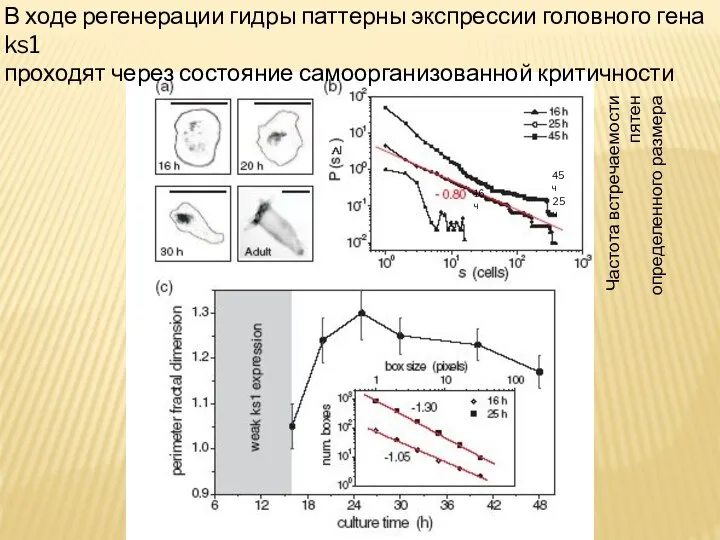
- 32. Частота встречаемости пятен определенного размера 16 ч 25ч 45 ч В ходе регенерации гидры паттерны экспрессии
- 33. ФРАКТАЛЫ
- 34. -сложная геометрическая фигура, обладающая свойством самоподобия, т.е. составленная из нескольких частей, каждая из которых подобна всей
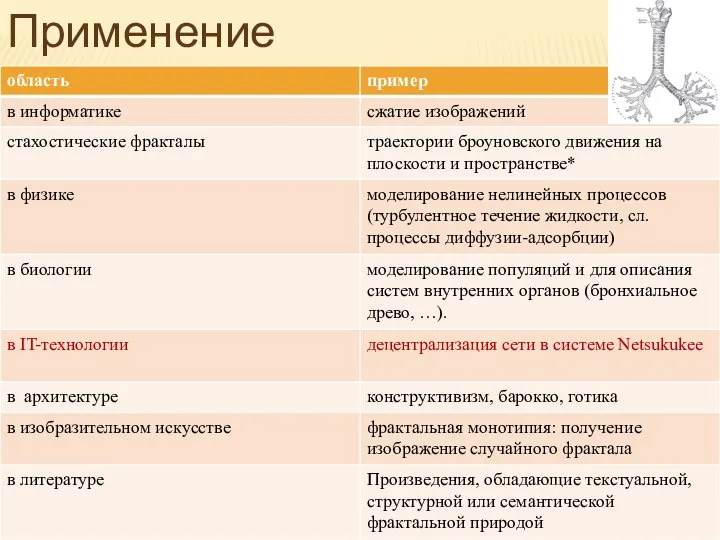
- 35. Применение
- 36. Бенуа Мандельброт (1980) С. Кранц: Р. Брукс, Дж. Мателски (1978) Дж. Хаббард (1976)- Ф.Кочмен Ф. Рисс
- 37. 20.11.1924 – 14.10.2010 С/х Химия Математика Медицина Физика Искусство Мать: Белла Лурие Отец: Карл Мандельброт Дядя:
- 40. «Природа демонстрирует совсем другой уровень сложности» Мандельброт Б., «Фрактальная геометрия природы», 1975 год. ?
- 41. 1) нетривиальная структура на всех масшатабах, повышение масштаба для фрактальных фигур не ведет к упрощению структуры;
- 42. 1) задать произвольную ломаную с конечным числом звеньев; 2) заменить в ней каждый отрезок генератором (точнее,
- 43. Мера Минковского
- 44. -множество точек в евклидовом пространстве, имеющие дробную метрическую размерность. Фрактал - это Под микроскопом он открыл,
- 47. Скачать презентацию



















 Задача по физике. Задания к открытому уроку математика + физика
Задача по физике. Задания к открытому уроку математика + физика 7_Sily_v_prirode_sila_tyazhesti_ves (1)
7_Sily_v_prirode_sila_tyazhesti_ves (1) Динамика материальной точки. Лекция 3
Динамика материальной точки. Лекция 3 Технічне обслуговування та наладка верстату HAAS EC-400
Технічне обслуговування та наладка верстату HAAS EC-400 Закон Кеплера
Закон Кеплера Электрическое сопротивление
Электрическое сопротивление Работа измерительного прибора ИРК-ПРО
Работа измерительного прибора ИРК-ПРО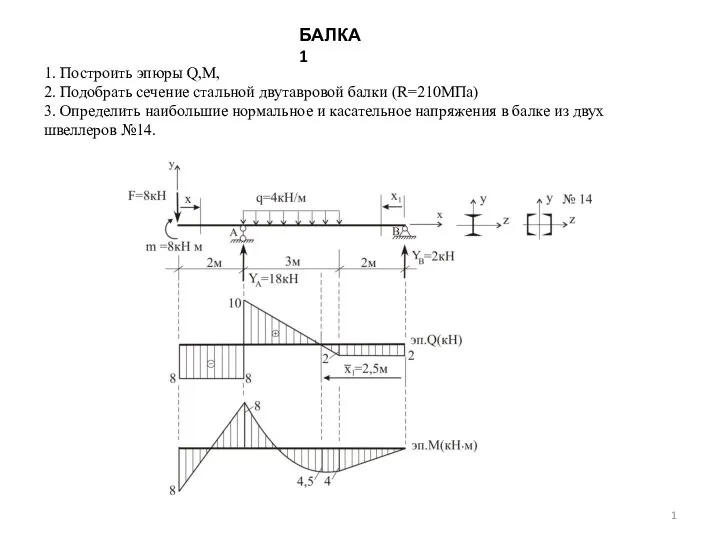 Расчет балки
Расчет балки Физика элементарных частиц
Физика элементарных частиц Электростатика. Электрические взаимодействия
Электростатика. Электрические взаимодействия Свет. Источники света
Свет. Источники света Уравнение неразрывности. Лекция 5
Уравнение неразрывности. Лекция 5 Электрический ток. Источники тока
Электрический ток. Источники тока Ультразвук. Понятие ультразвук
Ультразвук. Понятие ультразвук Полный цикл изготовления телескопов в домашних условиях
Полный цикл изготовления телескопов в домашних условиях Квазистационарное электромагнитное поле
Квазистационарное электромагнитное поле Термоядерный синтез
Термоядерный синтез Конструкция механизма Ланчестера
Конструкция механизма Ланчестера Типы соединений потребителей тока
Типы соединений потребителей тока Презентация на тему Решение задач по физике
Презентация на тему Решение задач по физике  Трение в природе, технике, быту
Трение в природе, технике, быту Термодинамическая работа
Термодинамическая работа Развитие представлений о строении атома. Модель резерфорда
Развитие представлений о строении атома. Модель резерфорда Упругие свойства среды. Лекция 1.13
Упругие свойства среды. Лекция 1.13 ВКР: Метод инфракрасной спектроскопии в целях судебной пожарно-технической экспертизы
ВКР: Метод инфракрасной спектроскопии в целях судебной пожарно-технической экспертизы Расчет амплитудно-частотных характеристик фильтров
Расчет амплитудно-частотных характеристик фильтров Волокна большого диаметра. Анализ фазового состава, макро- и микроструктуры полуфабрикатов и готовых изделий из B-Al
Волокна большого диаметра. Анализ фазового состава, макро- и микроструктуры полуфабрикатов и готовых изделий из B-Al Май күпдеші озған өткізгіш материал және оның парамтрі
Май күпдеші озған өткізгіш материал және оның парамтрі