Содержание
- 2. ПРЕДМЕТ И ЗАДАЧИ ДИНАМИКИ Динамикой называется раздел механики, в котором изучается движение механических систем под действием
- 3. Аксиомы динамики принцип инерции и принцип относительности Галилея, закон равенства действия и противодействия, основной закон динамики
- 4. Аксиома 1. (закон или принцип инерции) система сил, приложенная к материальной точке, является уравновешенной, если под
- 5. Понятия 1 аксиомы Материальная точка, которая не испытывает силовых воздействий со стороны других точек и тел,
- 6. Понятия 1 аксиомы Движение, которое совершает точка при отсутствии сил, называется движением по инерции. Инерционными системами
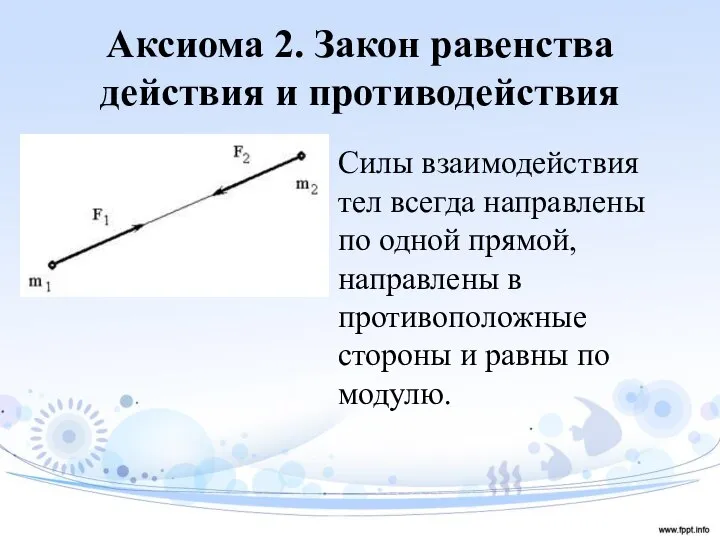
- 7. Аксиома 2. Закон равенства действия и противодействия Силы взаимодействия тел всегда направлены по одной прямой, направлены
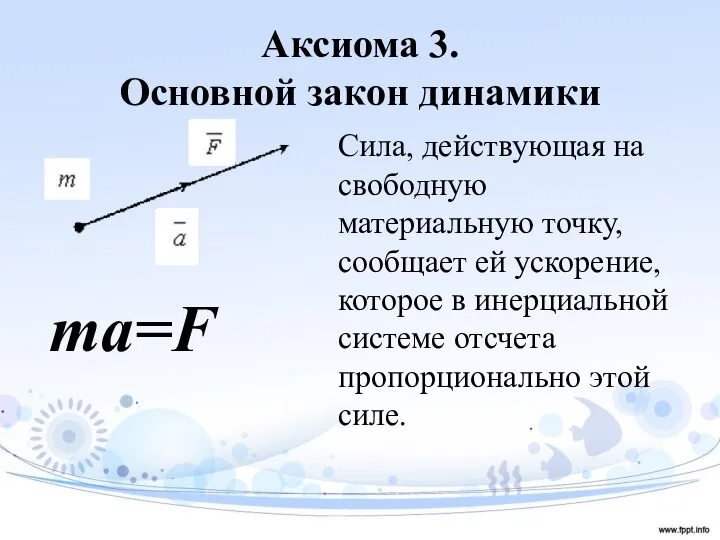
- 8. Аксиома 3. Основной закон динамики Сила, действующая на свободную материальную точку, сообщает ей ускорение, которое в
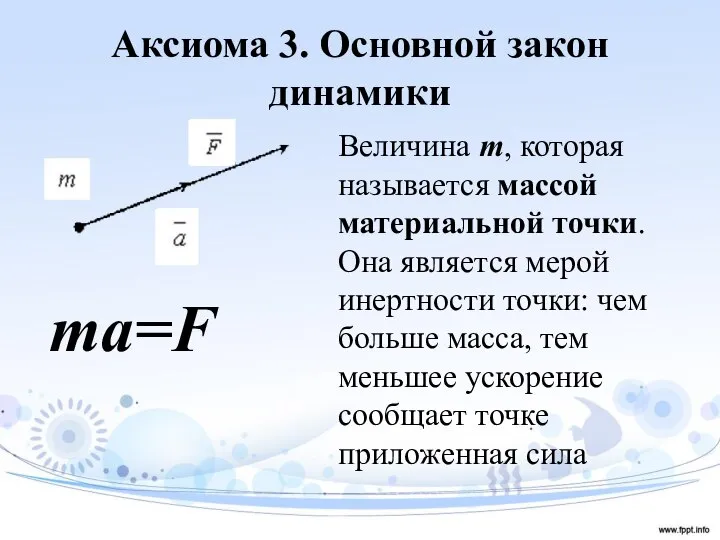
- 9. Аксиома 3. Основной закон динамики Величина m, которая называется массой материальной точки. Она является мерой инертности
- 10. Примечания: Если на точку действует несколько сил, то под F в уравнении следует понимать их равнодействующую:
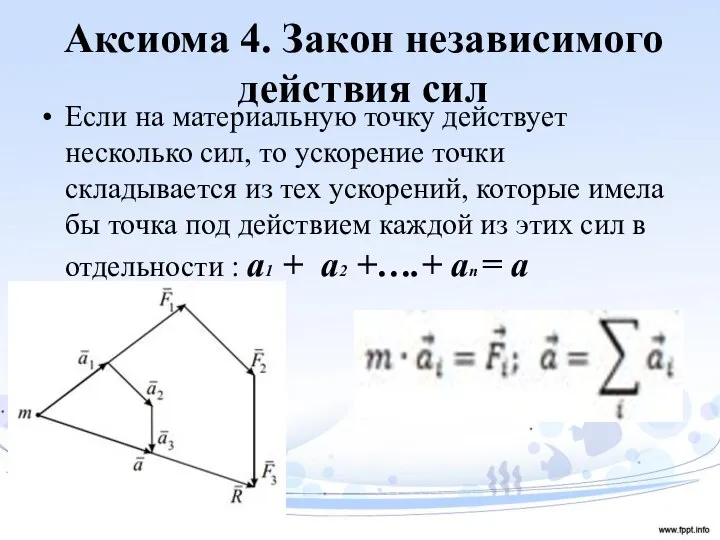
- 11. Аксиома 4. Закон независимого действия сил Если на материальную точку действует несколько сил, то ускорение точки
- 12. Идеальные и реальные связи Если связь препятствует перемещению тела в двух взаимно противоположных направлениях, то она
- 13. Идеальные и реальные связи Если связь препятствует перемещению в противоположном направлении, но допускает перемещение в противоположном
- 14. Идеальные и реальные связи При определении реакций связей предполагают, что в них нет трения, реакции при
- 15. Принцип Даламбера
- 16. Принцип Даламбера
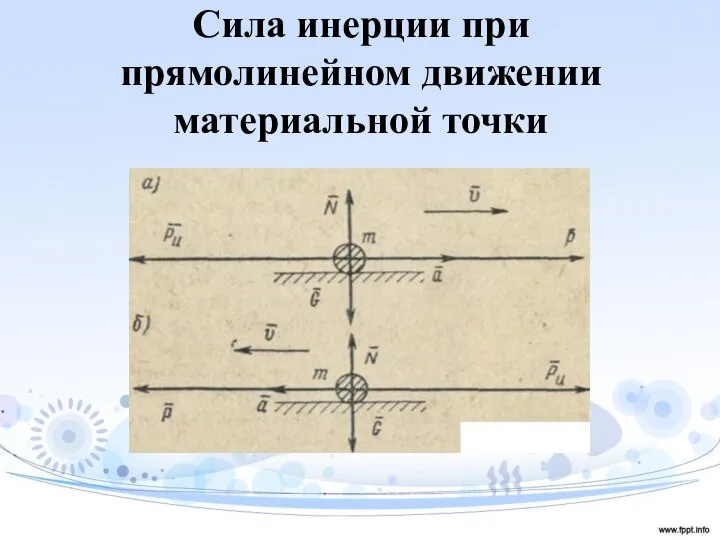
- 17. Сила инерции при прямолинейном движении материальной точки
- 18. Сила инерции при прямолинейном движении материальной точки
- 19. Сила инерции при прямолинейном движении материальной точки
- 20. Сила инерции при криволинейном движении материальной точки
- 21. Сила инерции при криволинейном движении материальной точки
- 22. Работы силы Работой силы А при прямолинейном перемещении точки ее приложения называется произведение величины силы Р
- 23. Работы силы Когда сила с направлением перемещения составляет острый угол, она называется движущей силой, ее работа
- 24. Случаи определения работы постоянной силы: - сила F действует на тело в направлении вектора перемещения U/А
- 25. Теоремы работы силы Теорема 1. Работа равнодействующей силы на некотором перемещении равна алгебраической сумме работ составляющих
- 26. Работа силы тяжести 1. Работа силы тяжести равна произведению силы тяжести на вертикальное перемещение ее точки
- 27. Работа силы тяжести 2. Работа силы тяжести зависит только от начального и конечного положений точки приложения
- 28. Работа упругой силы Упругая сила, возникающая в деформируемом теле, пропорциональна перемещению точки приложения силы от некоторого
- 29. Мощность. Коэффициент полезного действия Мощностью называется работа, совершаемая силой в течение единицы времени, т.е. мощность есть
- 30. Мощность. Коэффициент полезного действия Отношение работы сил полезных сопротивлений Апс (полезной работы) к работе движущих сил
- 31. Коэффициент потерь: Машина движется и выполняет полезную работу при 1 >ή > 0 2. Работа в
- 33. Скачать презентацию

























 Тест Поверхностное натяжение
Тест Поверхностное натяжение Газовые законы
Газовые законы Коробки передач. Рабочие процессы
Коробки передач. Рабочие процессы Теория упругости. Основные положения, допущения и обозначения
Теория упругости. Основные положения, допущения и обозначения Вклад советских учёных-физиков в Великую Победу
Вклад советских учёных-физиков в Великую Победу Описание устройства и работы системы питания МТЗ-80
Описание устройства и работы системы питания МТЗ-80 Urok_8
Urok_8 Исследование тепловых процессов в гетероинтегрированных многокристальных микромодулях на основе кремния для СВЧ применений
Исследование тепловых процессов в гетероинтегрированных многокристальных микромодулях на основе кремния для СВЧ применений Потенциальная энергия заряженного тела в однородном электростатическом поле
Потенциальная энергия заряженного тела в однородном электростатическом поле Идеальный газ в молекулярно-кинетической теории
Идеальный газ в молекулярно-кинетической теории Презентация на тему Вакуумные приборы
Презентация на тему Вакуумные приборы  Релейная защита
Релейная защита Механические колебания
Механические колебания Тепловые двигатели
Тепловые двигатели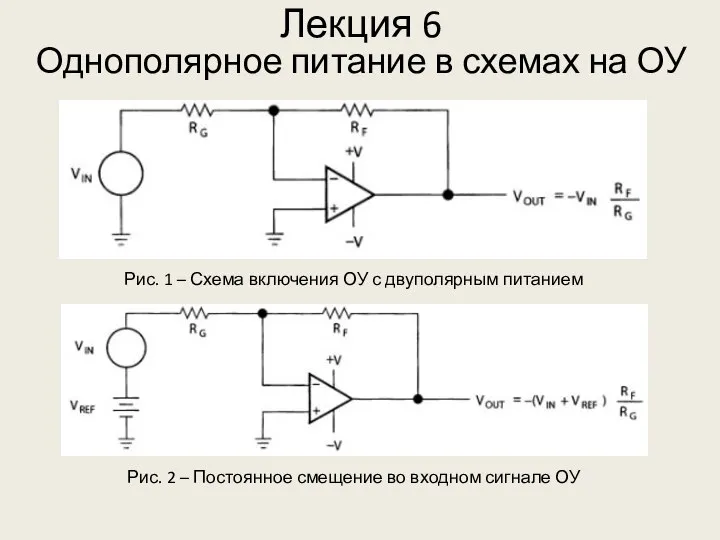 Однополярное питание в схемах на ОУ. (Лекция 6)
Однополярное питание в схемах на ОУ. (Лекция 6) Механик тирбәнеш, дулкыннар. Тавыш
Механик тирбәнеш, дулкыннар. Тавыш Наладка станка на обработку детали Фланец нажимной и кодирование управляющей программы
Наладка станка на обработку детали Фланец нажимной и кодирование управляющей программы Электрический ток
Электрический ток Tesla
Tesla Оптика
Оптика Гармонические колебания
Гармонические колебания Манометры Поршневой жидкостный насос. Гидравлический пресс (7 класс)
Манометры Поршневой жидкостный насос. Гидравлический пресс (7 класс) Оптичні ілюзії
Оптичні ілюзії Презентация ученицы 11 «А» класса Очеретиной Александры
Презентация ученицы 11 «А» класса Очеретиной Александры Решение задач по теме Длина волны. Скорость распространения волн
Решение задач по теме Длина волны. Скорость распространения волн Законы Ньютона
Законы Ньютона Разработка проекта устройства снижающего тяжесть последствий при потере устойчивости дорожных катков и компакторов
Разработка проекта устройства снижающего тяжесть последствий при потере устойчивости дорожных катков и компакторов Информационная подсистема пневмосистем. Тема 1.5
Информационная подсистема пневмосистем. Тема 1.5