способы решения
Система уравнений Максвелла для электромагнитного поля: смысл, способы решения
Полезно знать Подготовка к экзамену Физика для "чайников"
Иван27 Июнь 201717 264
Нет времени писать работу?
Доверь это кандидату наук!
Узнай стоимость
Содержание
Содержание
Первое уравнение Максвелла
Третье уравнение Максвелла
Второе уравнение Максвелла
Четвертое уравнение Максвелла
Уравнения Максвелла в электродинамике – это как законы Ньютона в классической механике или как постулаты Эйнштейна в теории относительности. Фундаментальные уравнения, в сущности которых мы сегодня будем разбираться, чтобы не впадать в ступор от одного их упоминания.
Уравнения Максвелла – это система уравнений в дифференциальной или интегральной форме, описывающая любые электромагнитные поля, связь между токами и электрическими зарядами в любых средах.
Уравнения Максвелла неохотно принимались и критически воспринимались учеными-современниками Максвелла. Все потому, что эти уравнения не были похожи ни на что из известного людям ранее.
Тем не менее, и по сей день нет никаких сомнений в правильности уравнений Максвелла, они «работают» не только в привычном нам макромире, но и в области квантовой механики.
Уравнения Максвелла совершили настоящий переворот в восприятии людьми научной картины мира. Так, они предвосхитили открытие радиоволн и показали, что свет имеет электромагнитную природу.
Квазистационарное электромагнитное поле












 Силы в механике. 9 класс
Силы в механике. 9 класс Урок-конференция Радиация и ее воздействия на биологические объекты Учитель Прокопец Н.Д.
Урок-конференция Радиация и ее воздействия на биологические объекты Учитель Прокопец Н.Д. Направление индукционного тока. Правило Ленца (9 класс)
Направление индукционного тока. Правило Ленца (9 класс) Силы в природе (7 класс)
Силы в природе (7 класс) Автоматическое регулирования и теплотехнический контроль параметров регенеративных подогревателей низкого давления турбоагрегата
Автоматическое регулирования и теплотехнический контроль параметров регенеративных подогревателей низкого давления турбоагрегата Напряженность электрического поля. Урок 52
Напряженность электрического поля. Урок 52 Что изучает физика? (7 класс)
Что изучает физика? (7 класс) Силы, действующие в магнитном поле: сила Ампера, сила Лоренца
Силы, действующие в магнитном поле: сила Ампера, сила Лоренца Презентация на тему Рентгеновские лучи
Презентация на тему Рентгеновские лучи  Строение атома. Опыт Резерфорда
Строение атома. Опыт Резерфорда Урок 7
Урок 7 Движение тела по окружности с постоянной по модулю скорости
Движение тела по окружности с постоянной по модулю скорости Разряд вдоль поверхности твердого диэлектрика. Лекция 4
Разряд вдоль поверхности твердого диэлектрика. Лекция 4 Экологическое воспитание на внеурочных занятиях по физике
Экологическое воспитание на внеурочных занятиях по физике Досліди Фарадея. Явище електромагнітної індукції. 9кл
Досліди Фарадея. Явище електромагнітної індукції. 9кл Пословицы и поговорки о законах механики
Пословицы и поговорки о законах механики Низкоэнергетическое лазерное излучение
Низкоэнергетическое лазерное излучение Влияние электромагнитного излучения на организм и здоровье человека
Влияние электромагнитного излучения на организм и здоровье человека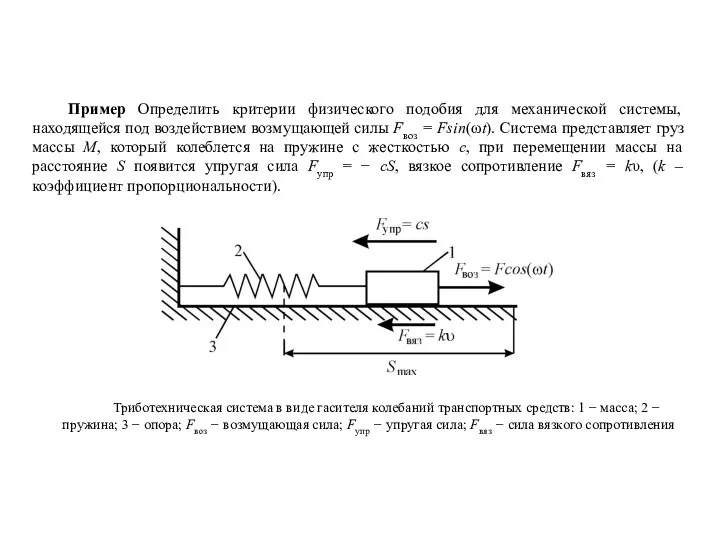 Определение критериев физического подобия для механической системы
Определение критериев физического подобия для механической системы Изменения школьного процесса обучения физике в условиях обновления образования
Изменения школьного процесса обучения физике в условиях обновления образования Организация проектно-исследовательской деятельности на уроках физики как путь к формированию ключевых компетенций
Организация проектно-исследовательской деятельности на уроках физики как путь к формированию ключевых компетенций Уравнение состояния идеального газа
Уравнение состояния идеального газа Презентация на тему Кабинет физики
Презентация на тему Кабинет физики  Атомные столкновения и спектрометрия обратного рассеяния
Атомные столкновения и спектрометрия обратного рассеяния Период, частота и амплитуда переменного тока
Период, частота и амплитуда переменного тока Теоретические основы электротехники
Теоретические основы электротехники Методы астрофизических исследований. Занятие 11
Методы астрофизических исследований. Занятие 11 Нелинейные электрические цепи
Нелинейные электрические цепи