Содержание
- 2. план 1-Ньютон и Лейбниц 2- теорема 3- интеграл 4- применение интеграла 5-историческое значение и философский смысл
- 3. Ньютон Лейбниц
- 4. Ньютон и Лейбниц Из сохранившихся документов историки науки выяснили, что дифференциальное и интегральное исчислениеИз сохранившихся документов
- 5. Вняв уговорам друзей, взывавших к его патриотизму, Ньютон во 2-й книге своих «Начал» (1687) сообщил:[71] В
- 6. В 1693 году, когда Ньютон наконец опубликовал первое краткое изложение своей версии анализа, он обменялся с
- 7. После появления первой подробной публикации ньютонова анализа (математическое приложение к «Оптике», 1704После появления первой подробной публикации
- 8. 31 января31 января 1713 года Королевское общество получило письмо от Лейбница, содержащее примирительную формулировку: он согласен,
- 9. В ответ с лета 1713 года Европу наводнили анонимные брошюры, которые отстаивали приоритет Лейбница и утверждали,
- 10. теорема Теорема Если f непрерывна на отрезке a,b и Ф — ее любая первообразная на этом
- 11. Доказательство Пусть на отрезке (a,b) задана интегрируемая функция ʄ Начнем с того, что отметим, что то
- 12. Зададим произвольное значение x € (a.b) и определим новую функцию Она определена для всех значений x
- 13. Заметим, что Покажем, что F непрерывна на отрезке (a,b) В самом деле, пусть тогда и если
- 14. Таким образом , F непрерывна на (a,b) независимо от того, имеет или не имеет ʄ разрывы;
- 15. Пусть теперь функция ʄ не только интегрируема на (a,x) , но непрерывна в точке Докажем, что
- 16. Мы положили а так как ʄ (x) постоянная относительно t ,TO Далее, в силу непрерывности ʄ
- 17. Переход к пределу в при h→0 показывает существование производной от F в точке и справедливость равенства
- 18. Мы доказали, что произвольная непрерывная на отрезке (a,b) функция ʄ имеет на этом отрезке первообразную, определенную
- 19. Поэтому
- 20. Интеграл Интеграл функции — естественный аналог суммы последовательности. Согласно основной теореме анализа — естественный аналог суммы
- 21. Типы интегралов Определённый интеграл Неопределённый интеграл Интеграл РиманаИнтеграл Римана и Римана — Стилтьеса Интеграл ЛебегаИнтеграл Лебега
- 22. История Знаки интеграла ʃ дифференцирования dx были впервые использованы Лейбницембыли впервые использованы Лейбницем в конце XVII
- 23. Историческое значение и философский смысл формулы Ньютона-Лейбница Одним из важнейших исследовательских инструментов этого ряда является формула
- 24. Но дальнейший научный анализ дает в наше время новую, иную картину происходящего процесса. Ныне господствующие в
- 25. Даже мистические и магические течения должны считаться с этим положением, хотя они могут, придав иной смысл
- 26. Вместе с тем объема накопленных человечеством знаний уже вполне достаточно для того, что бы эту традицию
- 27. В свете вышесказанного, на современном этапе исторический анализ представляет собой математический анализ с теорией вероятности и
- 28. Собственно же формулу, ввиду особенности восприятия математических символов носителями социально-гуманитарного знания, выражающуюся в панической боязни этими
- 29. ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА: 1. Бродский И.А. Сочинения в четырех томах. Т.3. СПб., 1994. 2. Вернадский В.И. Биосфера
- 31. Скачать презентацию




























 Простые механизмы
Простые механизмы Мембранные процессы
Мембранные процессы Закон сохранения механической энергии
Закон сохранения механической энергии Снегоплавилка. Идея проекта
Снегоплавилка. Идея проекта Общий вид стационарной ЭТЛ
Общий вид стационарной ЭТЛ Стохастическое описание систем генной регуляции
Стохастическое описание систем генной регуляции Основы энергетики. Строение материи
Основы энергетики. Строение материи Геометрическое движение в физике
Геометрическое движение в физике Изготовление водородного генератора и изучение его рабочих характеристик
Изготовление водородного генератора и изучение его рабочих характеристик Как работают солнечные панели
Как работают солнечные панели Мобильный микроманипулятор для экстремальных климатических условий
Мобильный микроманипулятор для экстремальных климатических условий Плоская электромагнитная волна. Лекция 2с 7 (2)
Плоская электромагнитная волна. Лекция 2с 7 (2) Решение задач на силу Ампера и силу Лоренца. Урок 51
Решение задач на силу Ампера и силу Лоренца. Урок 51 Формирование у детей представления о физическом явлении. Звук
Формирование у детей представления о физическом явлении. Звук Вечный двигатель в истории
Вечный двигатель в истории Презентация на тему Тепловые машины и их КПД
Презентация на тему Тепловые машины и их КПД  Принципы и методы обработки результатов измерения физических величин
Принципы и методы обработки результатов измерения физических величин Презентация на тему Испарение и конденсация
Презентация на тему Испарение и конденсация  Построение эпюр поперечных сил и изгибающих моментов
Построение эпюр поперечных сил и изгибающих моментов Теоретические основы разработки полимерных композиционных материалов триботехнического назначения. Задание на КП
Теоретические основы разработки полимерных композиционных материалов триботехнического назначения. Задание на КП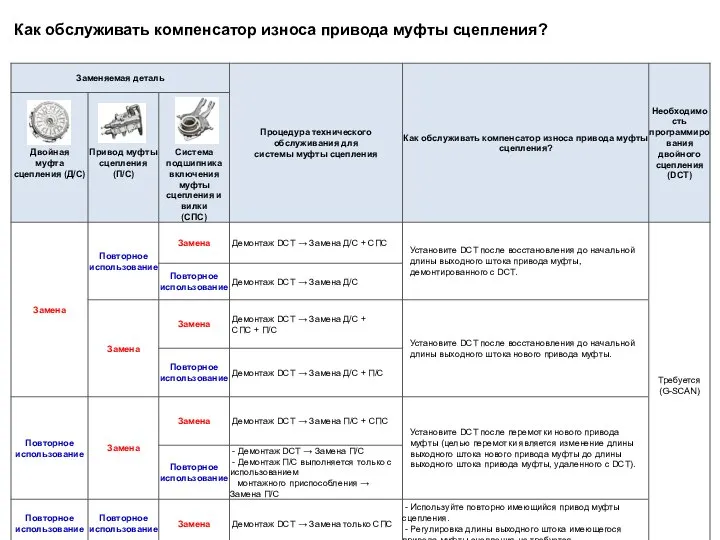 Как обслуживать компенсатор износа привода муфты сцепления
Как обслуживать компенсатор износа привода муфты сцепления Тема 1.4. Опиливание
Тема 1.4. Опиливание Что изучает физика
Что изучает физика Термическое разупрочнение деформированного металла
Термическое разупрочнение деформированного металла Ремонт типовых соединений и деталей
Ремонт типовых соединений и деталей Популярные типы кузова автомобилей
Популярные типы кузова автомобилей Выбираем тему исследования. Нанотехнологии
Выбираем тему исследования. Нанотехнологии Презентация на тему Оптические явления в атмосфере
Презентация на тему Оптические явления в атмосфере