prez_L3

Угловая скорость вращения

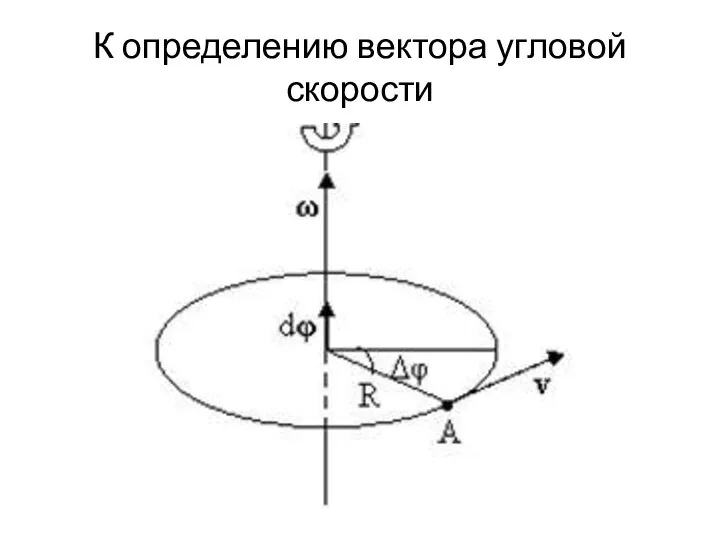
К определению вектора угловой скорости

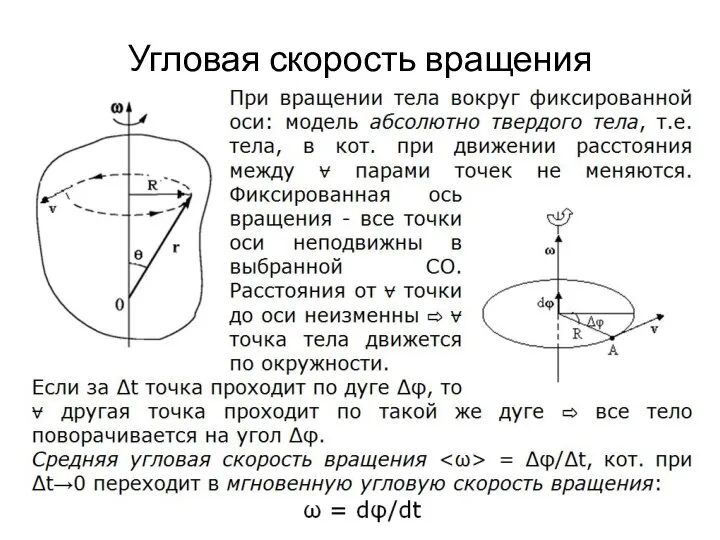
Векторы угловой скорости и углового ускорения

Динамика
Кинематика - траектории, скорости, ускорения, но не причины.
Динамика - раздел механики, изучающий причины движения. Динамика рассматривает движение тел с пом. модели, основные положения кот. можно сформулировать следующим образом:
1. если тело достаточно мало, то его движение подчиняется законам движения материальной точки (МТ);
2. основные законы движения МТ - 3 закона Ньютона (ЗН);
3. если тело большое, то его мысленно разбивают на части, каждую из которых можно считать МТ;
4. взаимодействие между частями крупного тела - с помощью тех же законов Ньютона.
Опыт ⇒ движение МТ полностью описывается 3 ЗН (конец 17 века, «Математические начала натуральной философии»).

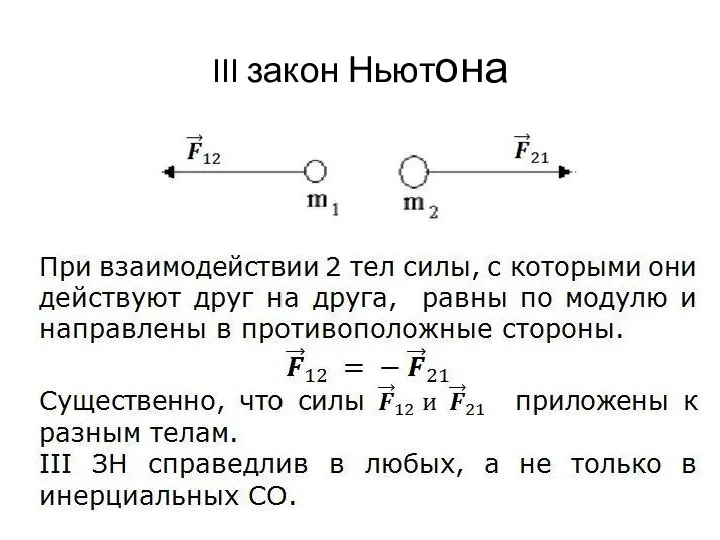
3 закона Ньютона
I. Всякое тело продолжает оставаться в состоянии покоя или равномерного прямолинейного движения пока и поскольку не понуждается приложенными силами изменить это состояние.
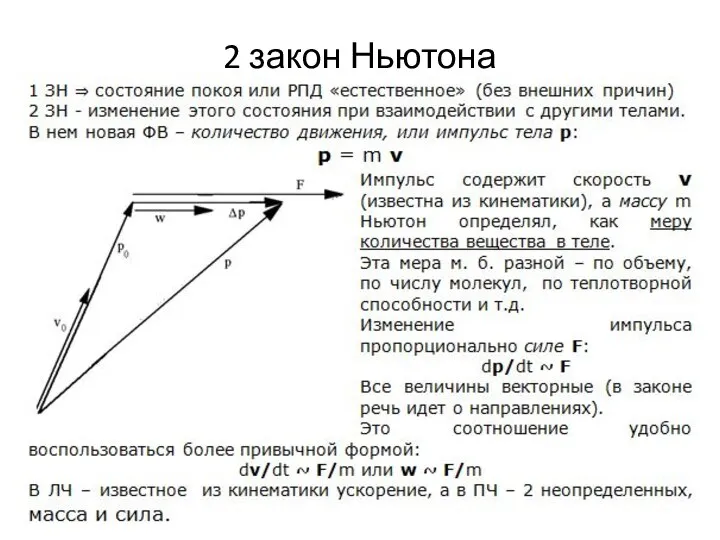
II Изменение количества движения тела происходит пропорционально действующей силе и по направлению той прямой, по которой приложена эта сила.
III Действию всегда есть равное и противоположно направленное противодействие, иначе - воздействия 2 тел друг на друга между собою равны и направлены в противоположные стороны.

Латынь из моды вышла ныне
Lex prima
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare.
Всякое тело продолжает оставаться в состоянии покоя или равномерного прямолинейного движения пока и поскольку не понуждается приложенными силами изменить это состояние.

1 закон Ньютона
Аристотель: естественное состояние ⩝ тела - состояние покоя. Чтобы привести тело в движение и поддерживать его, нужна внешняя причина (наз. силой). Сила исчезает ⇒ тело возвращается в состояние покоя.
Галилей (нач. 16 в.): нет принципиальной разницы между состояниями покоя и равномерного прямолинейного движения (РПД). Если корабль движется равномерно и прямолинейно относительно берега, то тело покоится на его палубе, но движется равномерно и прямолинейно относительно берега.
Все физические процессы в СО протекают одинаково, независимо от того, неподвижна система или находится в состоянии РПД.
Это (принцип относительности Галилея), уравнивает состояния покоя и равномерного прямолинейного движения и является частью 1 ЗН.
Второй смысл этого закона - при рассмотрении 2 ЗН.

2 закон Ньютона

Понятия силы и массы
Сила? Ньютон: тело испытывает ускорение ⇒ на него воздействуют другие тела, а мерой этого воздействия является ФВ – сила. Происхождение м. б. разным.
Как сравнивать разные силы?
Масса? Ньютон: мера количества вещества в теле, чем больше в теле вещества, тем меньшее ускорение оно получит.
Эйлер (около 1740): масса - мера инертности тела, т.е. способности сохранять свою скорость под воздействием силы.

Масса
2 тела получают одинаковое ускорение под действием одной и той же силы ⇒ у них одинаковая масса.
Масса - особая ФВ ⇒ нужна единица измерения, т.е. нужно указать тело, масса которого считается единичной.
В СИ: единица массы килограмм (кг) - масса 1 дм3 чистой воды при 4оС и нормальном давлении. [m] = кг
Эталон из сплава платины и иридия.
Диапазон: от 10-30 кг для электрона до 1042 кг для Галактики (человек – 102 кг, Земля – 1025 кг, Солнце - 1030 кг).

Единицы для силы и импульса

Соотношение I и II законов Ньютона
1-е заблуждение: I ЗН не самостоятельный закон, а частный случай II ЗН при F = 0.
2-е заблуждение: II ЗН противоречит простым наблюдениям: если наблюдатель движется с ускорением, то окружающие предметы движутся с ускорением в противоположную сторону.
II ЗН справедлив не для всех систем отсчета, а только для некоторых из них, а именно, для инерциальных СО (ИСО).
Существуют ли ИСО?
Ответы дает I ЗН. Признак ИСО w = 0 при F = 0. Существование таких CO обещает 1 ЗН. В этом состоит второй важный смысл 1 ЗН.
Принцип относительности утверждает, что все СО, движущиеся равномерно и прямолинейно друг относительно друга, эквивалентны, т.е. если существует одна ИСО, то существует и бесконечное множество других.

Система отсчета

III закон Ньютона

Динамические уравнения движения.
(обратная задача динамики)
Законы Ньютона ⇨
дифференциальные уравнения (ДУ) = динамические уравнения движения.
Решения динамических уравнений движения ⇨
кинематические уравнения движения,
т.е. зависимости от времени координат и скоростей тел.

Простой пример

Константы интегрирования и начальные условия
Решение с конст-ми интегрирования – общее решение.
Константы интегрирования ⇦ начальные условия (НУ). т.е. значения vx и х в начальный момент времени.
Их подставить в общее решение и найти С:
vx = (Fx /m) t + v0
x = ½(Fx /m) t2 + v0 t + x0
Решение ДУ (и систем ДУ, т.к. нужны еще уравнения для 2 других координат и для других тел) требует некоторых математических навыков.
Поэтому стараются избегать ДУ и получать решения из законов сохранения (ЗС), т.е. соотношений для ФВ, которые сохраняют свои начальные значения при некоторых условиях.

Закон сохранения импульса

Закон сохранения импульса для замкнутой системы

Закон сохранения и изменения импульса незамкнутой системы