Слайд 2План :
1. Схема решения задач на приложения определенного интеграла
2. Нахождение пути, пройденного

телом при прямолинейном движении
3. Вычисление работы силы, произведенной при прямолинейном движении тела
4. Вычисление работы, затраченной на растяжение или сжатие пружины
5. Определение силы давления жидкости на вертикально расположенную пластинку
Слайд 3немного … теории
по данной теме

Слайд 41. Схема решения задач на приложения определенного интеграла
С помощью определенного интеграла можно

решать различные задачи физики, механики и т. д., которые трудно или невозможно решить методами элементарной математики.
Так, понятие определенного интеграла применяется при решении задач на вычисление работы переменной силы, давления жидкости на вертикальную поверхность, пути, пройденного телом, имеющим переменную скорость, и ряд других.
Несмотря на разнообразие этих задач, они объединяются одной и той же схемой рассуждений при их решении. Искомая величина (путь, работа, давление и т. д.) соответствует некоторому промежутку изменения переменной величины, которая является переменной интегрирования. Эту переменную величину обозначают через Х, а промежуток ее изменения — через [а, b].
Отрезок [a, b] разбивают на n равных частей, в каждой из которых можно пренебречь изменением переменной величины. Этого можно добиться при увеличении числа разбиений отрезка.
На каждой такой части задачу решают
по формулам для постоянных величин.
Далее составляют сумму (интегральную
сумму), выражающую приближенное
значение искомой величины. Переходя к
пределу при n→∞, находят искомую
величину I в виде интеграла
Слайд 52. Нахождение пути, пройденного телом при прямолинейном движении
Как известно, путь, пройденный телом
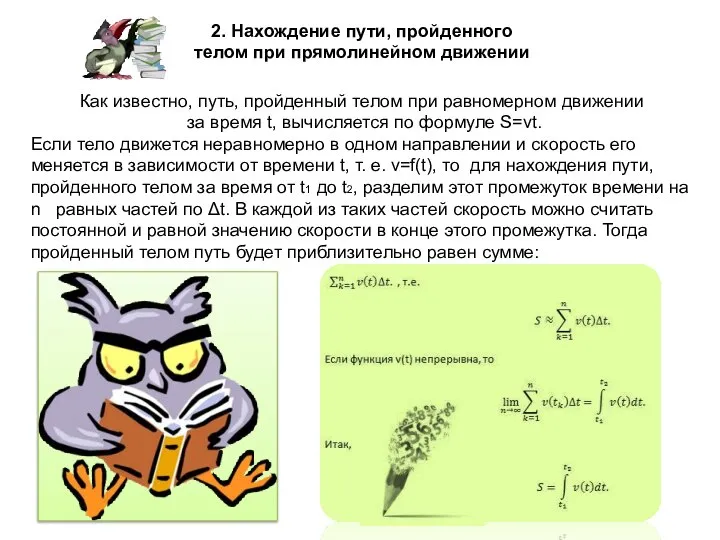
при равномерном движении
за время t, вычисляется по формуле S=vt.
Если тело движется неравномерно в одном направлении и скорость его меняется в зависимости от времени t, т. е. v=f(t), то для нахождения пути, пройденного телом за время от t1 до t2, разделим этот промежуток времени на n равных частей по Δt. В каждой из таких частей скорость можно считать постоянной и равной значению скорости в конце этого промежутка. Тогда пройденный телом путь будет приблизительно равен сумме:
Слайд 63. Вычисление работы силы, произведенной
при прямолинейном движении тела

Слайд 74.Вычисление работы, затраченной на растяжение или сжатие пружины

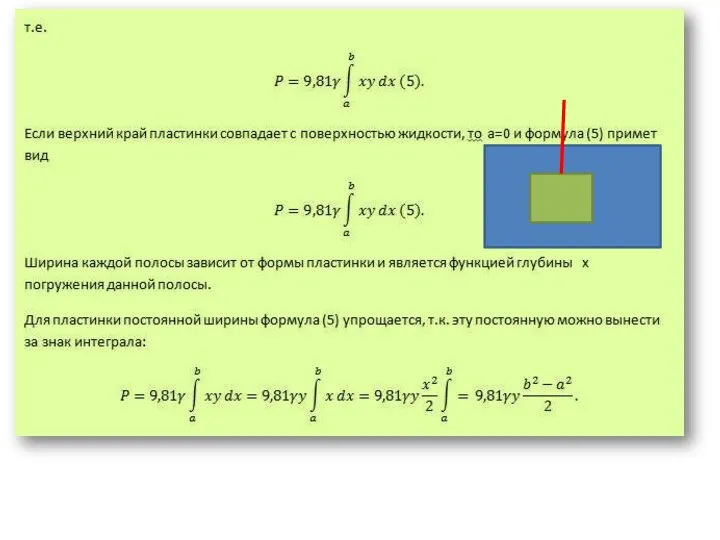
Слайд 85.Определение силы давления жидкости на вертикально расположенную пластинку

Слайд 10Рассмотрим примеры задач по данной теме
№ 1

Слайд 18№ 5
Какую работу совершает сила в 10Н при растяжении пружины на 2

см?
Слайд 20№ 6
Сила в 60Н растягивает пружину на 2 см. Первоначальная длина пружины

равна 14 см. Какую работу нужно совершить, чтобы растянуть ее до 20 см?
Слайд 22№ 7
Определить силу давления воды на стенку шлюза, длина которого 20 м,

а высота 5 м (считая шлюз доверху заполненным водой).
Слайд 24№ 8
В воду опущена прямоугольная пластинка, расположенная вертикально. Ее горизонтальная сторона равна

1 м, вертикальная 2 м. Верхняя сторона находится на глубине 0,5 м. Определить силу давления воды на пластинку.
Слайд 32№ 12
Вычислить силу давления воды на плотину, имеющую форму трапеции, у которой

верхнее основание, совпадающее с поверхностью воды, имеет длину 10 м, нижнее основание 20 м, а высота 3 м.




















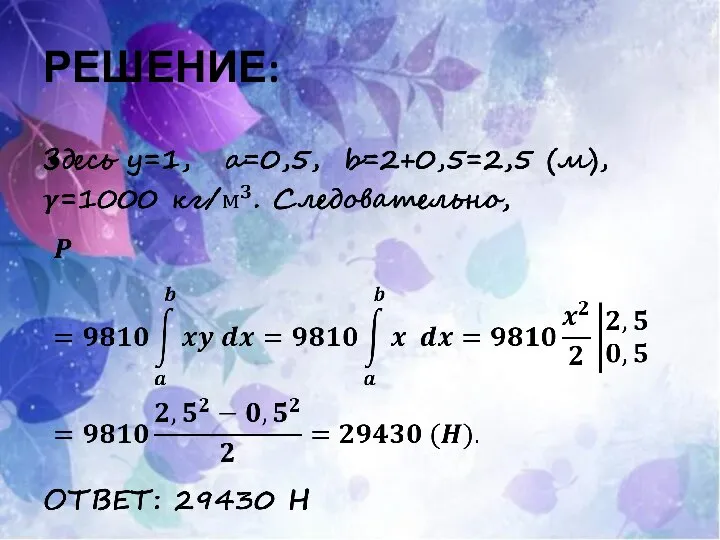







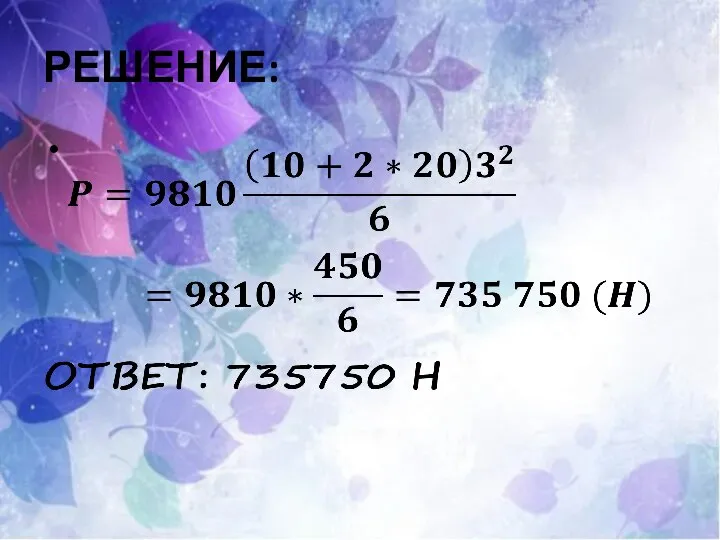


 Тест по теме Радио
Тест по теме Радио Презентация на тему Пластмассы и каучуки
Презентация на тему Пластмассы и каучуки  Состав ядра атома
Состав ядра атома Презентация на тему Философские аспекты физики в работах М.А.Маркова
Презентация на тему Философские аспекты физики в работах М.А.Маркова  Термодинамика диэлектриков. Типы диэлектриков, свойства и применение
Термодинамика диэлектриков. Типы диэлектриков, свойства и применение Физические и химические явления. 8 класс
Физические и химические явления. 8 класс Наблюдение сплошного и линейчатых спектров. Лабораторная работа
Наблюдение сплошного и линейчатых спектров. Лабораторная работа Открытый урок по физике. Основной закон электростатики - закон Кулона
Открытый урок по физике. Основной закон электростатики - закон Кулона Основы молекулярной физики и термодинамики. Лекция 4
Основы молекулярной физики и термодинамики. Лекция 4 Механическое движение
Механическое движение Динамика моря и Условия судоходства
Динамика моря и Условия судоходства Параллельная работа двух разных центробежных насосов
Параллельная работа двух разных центробежных насосов Лекция 7. Расчет статически неопределимых систем методом сил
Лекция 7. Расчет статически неопределимых систем методом сил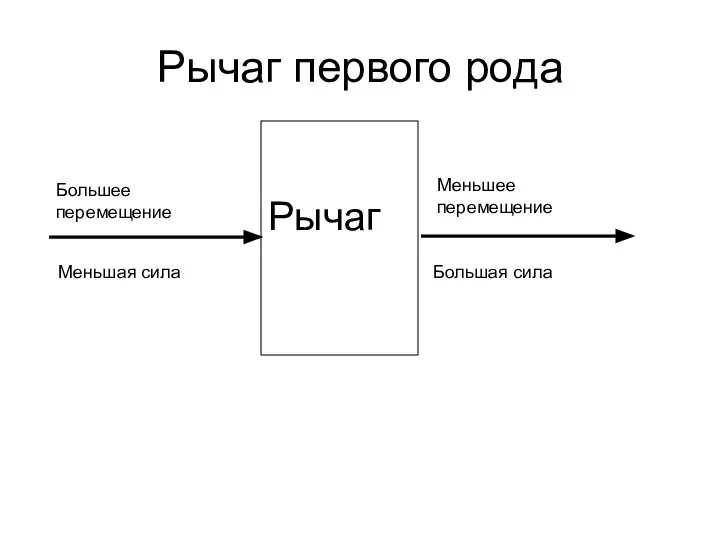 Рычаг первого рода
Рычаг первого рода Основы электричества
Основы электричества Статистическая теория радиотехнических систем. Нормальный случайный процесс. (Лекция 7)
Статистическая теория радиотехнических систем. Нормальный случайный процесс. (Лекция 7) Теория относительности. (Лекция 1)
Теория относительности. (Лекция 1) Тепловые явления. Интеллектуальная игра по физике для 8-х классов
Тепловые явления. Интеллектуальная игра по физике для 8-х классов Условия равновесия тел. Виды равновесия
Условия равновесия тел. Виды равновесия Механическое движение (7 класс)
Механическое движение (7 класс) Прибор для демонстрации инерции
Прибор для демонстрации инерции Естествознание как источник развития техники
Естествознание как источник развития техники Внутренняя энергия и способы ее изменения
Внутренняя энергия и способы ее изменения Давление
Давление Закон радиоактивного распада. Решение задач
Закон радиоактивного распада. Решение задач Лазер, устройство лазера
Лазер, устройство лазера Правила Кирхгофа. Тема 12
Правила Кирхгофа. Тема 12 Презентация (4)
Презентация (4)