Программа расчета и проведение компьютерного моделирования прохождения электронов через многобарьерную потенциальную структуру

ЗАДАНИЕ НА КУРСОВОЙ ПРОЕКТ
Разработать программу расчета и провести компьютерное моделирование прохождения электронов через многобарьерную потенциальную структуру:
Привести основные сведения о потенциальных структурах (ступеньки, ямы, барьеры, многоэлементные структуры и т.д.) и технологии их получения.
Привести основные сведения о практическом применении потенциальных структур в электронной и лазерной технике.
Записать основные формулы решения уравнения Шредингера для многобарьерной потенциальной структуры.

ПОТЕНЦИАЛЬНАЯ СТРУКТУРА
Потенциальная структура, или потенциальный рельеф — распределение электрических полей на поверхности или в объеме материала.
Низкоразмерная структура – структура, один из геометрических размеров которой меньше длины волны де Бройля для электрона в данном материале.

ОСНОВНЫЕ ПОТЕНЦИАЛЬНЫЕ СТРУКТУРЫ
В данной работе рассматривается несколько потенциальных структур:
1. Потенциальная ступенька
2. Потенциальная яма
3. Потенциальный барьер
4. Многобарьерная структура

ПОТЕНЦИАЛЬНАЯ СТУПЕНЬКА
5
Рис. 1 - Потенциальная ступенька
Потенциальная ступень — простейший тип потенциального рельефа. Поскольку высота потенциальной ступени постоянна, то поиск состояний движения частицы сводится к решению одномерного уравнения Шрёдингера:
В области 1 движение частицы ничем не ограничено и в результате решения уравнения получим:
В области 2:

ПОТЕНЦИАЛЬНАЯ ЯМА
6
Потенциальная яма — область пространства, где присутствует локальный минимум потенциальной энергии частицы.
Рис. 2 - Потенциальная яма
Квантовая яма, также называемая квантовым колодцем или потенциальной ямой — это потенциальная структура, ограниченная на некой области «стенками» потенциальных барьеров.

ПОТЕНЦИАЛЬНАЯ ЯМА
7
Если в потенциальную яму попала частица, энергия которой ниже, чем необходимая для преодоления краёв ямы, то возникнут колебания частицы в яме. Амплитуда колебаний будет обусловлена собственной энергией частицы. Частица, находящаяся на дне потенциальной ямы, пребывает в состоянии устойчивого равновесия, то есть при отклонении частицы от точки минимума потенциальной энергии возникает сила, направленная в противоположную отклонению сторону.
Рис. 3 - Энергетическая диаграмма квантовой (потенциальной) ямы: а – асимметричная, б – симметричная

ПОТЕНЦИАЛЬНАЯ ЯМА
8
Если частица подчиняется квантовым законам, то даже несмотря на недостаток энергии она с определённой
вероятностью может покинуть потенциальную яму (явление туннельного эффекта).
Туннельный эффект обусловлен требованием непрерывной волновой функции на стенках потенциальной ямы.
С увеличением высоты и ширины ямы вероятность туннельного эффекта экспоненциально спадает. Вероятность туннельного эффекта также быстро убывает с увеличением массы частицы.
Рис. 4 - Энергетическая диаграмма квантовой ямы с конечными (а) и бесконечными (б) стенками и дополнительным потенциальным провалом.

ПОТЕНЦИАЛЬНЫЙ БАРЬЕР
Потенциальный барьер – область пространства, где потенциальная энергия частицы (или тела) выше, чем в соседних областях.(противоположно квантовой яме)
Рассмотрим простейший потенциальный барьер прямоугольной формы шириной а и высотой U0. Вне барьера потенциальная энергия частицы равна нулю. Полная энергия частицы Е равна сумме её кинетической энергии Т и потенциальной U. Вне барьера Е = Т. Если частица двигается на барьер слева и имеет Е = Т < U0, то с точки зрения классической физики она не может преодолеть его и отразится от него.
Рис. 5 - Прямоугольный потенциальный барьер и туннельный эффект: j1 – поток частиц, падающих на барьер, j2 – поток отражённых частиц, j3 – поток прошедших частиц.

ПОТЕНЦИАЛЬНЫЙ БАРЬЕР
Если представить, что частица с Е < U0, вошла внутрь барьера, то она неизбежно должна иметь там отрицательную кинетическую энергию (чтобы её полная энергия сохранилась), что невозможно по смыслу кинетической энергии.
С точки зрения квантовой физики частица с Е < U0 может с некоторой вероятностью пройти сквозь барьер. Это явление носит название туннельного эффекта.

ПОТЕНЦИАЛЬНЫЙ БАРЬЕР
Коэффициент прохождения через барьер определяется:
Отметим, что коэффициенты прохождения и отражения симметричны. Это означает что проницаемость барьера одинакова для потоков справа и слева.
В пример возьмем уже полученные коэффициенты прохождения и отражения для несимметричного барьера.

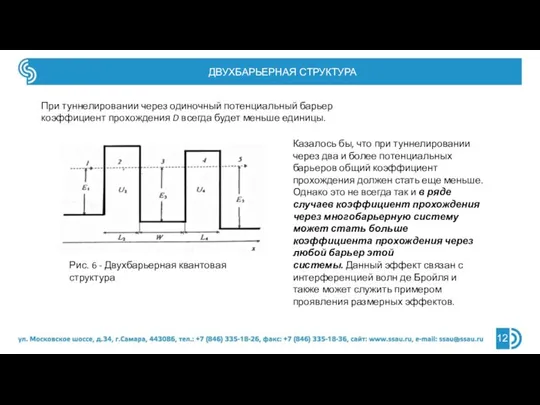
ДВУХБАРЬЕРНАЯ СТРУКТУРА
Рис. 6 - Двухбарьерная квантовая структура
Казалось бы, что при туннелировании через два и более потенциальных барьеров общий коэффициент прохождения должен стать еще меньше. Однако это не всегда так и в ряде случаев ко­эффициент прохождения через многобарьерную систему может стать больше коэффициента прохождения через любой барьер этой системы. Данный эффект связан с интерференцией волн де Бройля и также может служить примером проявления размерных эффектов.
При туннелировании через одиночный потенциаль­ный барьер коэффициент прохождения D всегда будет меньше единицы.

ДВУХБАРЬЕРНАЯ СТРУКТУРА
Рассмотрим прохождение частицы через систему из двух потенциальных барьеров.
Состояния движения частицы через эту систему могут быть найдены из решения одно­мерного уравнения Шредингера . Для энергий, соответст­вующих туннелированию частицы через оба барьера, решения в областях 1,3 и 5 можно записать в виде:
где
полагаем, что масса частицы во всех областях одинакова
Для областей 2 и 4:

МЕТОДЫ ПОЛУЧЕНИЯ ПОТЕНЦИАЛЬНЫХ СТРУКТУР
Квантовые ямы можно получить при использовании полупроводников с разной шириной запрещённой зоны (ЗЗ): если окружить полупроводник с узкой ЗЗ двумя слоями полупроводника с широкой ЗЗ, то гетеропереходы образуют стенки потенциальной ямы. Потенциальный барьер же можно получить, «инвертировав» конструкцию – окружив полупроводник с широкой ЗЗ полупроводником с узкой ЗЗ.
Рис. 7 - Формирование гетероперехода между полупроводниками с различной шириной запрещенной зоны

МЕТОДЫ ПОЛУЧЕНИЯ ПОТЕНЦИАЛЬНЫХ СТРУКТУР
15
Наилучшие результаты при создании потенциальных структур показывает молекулярно-лучевая эпитаксия (МЛЭ).
Рис. 8 - Выращивание КТ методом молекулярно-лучевой эпитаксии
Этот метод позволяет выращивать КТ на тщательно очищенных подложках (рис. 8). В условиях глубокого вакуума на подложку направляют поток атомов или молекул, получаемый испарением вещества со специально подготовленных источников. Если в качестве источников по очереди использовать вещества с различной шириной запрещенной зоны, можно вырастить на подложке характерную «пирамидку».

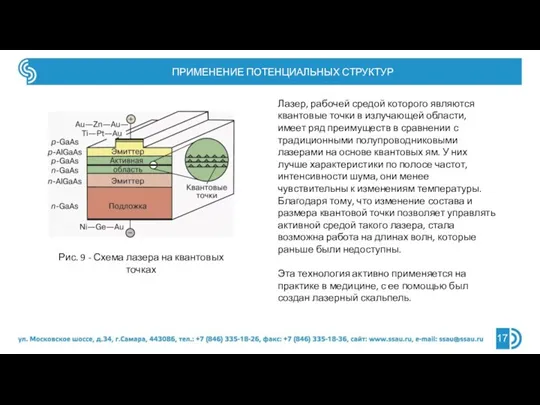
ПРИМЕНЕНИЕ ПОТЕНЦИАЛЬНЫХ СТРУКТУР
16
Квантовые структуры используются для создания лазеров. Уже сегодня эффективные лазерные устройства на квантовых ямах дошли до рынка и применяются в волоконно-оптических линиях связи. Для работы любого лазера необходимо создать инверсную населенность энергетических уровней. То есть, на более высоком уровне должно находиться больше электронов, чем на низком, в то время как в состоянии теплового равновесия ситуация обратная. Каждому лазеру необходим оптический резонатор или система зеркал, которая запирает электромагнитное излучение в рабочем объёме.
Рис.8 - Энергетическая схема лазера на квантовой яме

ПРИМЕНЕНИЕ ПОТЕНЦИАЛЬНЫХ СТРУКТУР
17
Лазер, рабочей средой которого являются квантовые точки в излучающей области, имеет ряд преимуществ в сравнении с традиционными полупроводниковыми лазерами на основе квантовых ям. У них лучше характеристики по полосе частот, интенсивности шума, они менее чувствительны к изменениям температуры.
Благодаря тому, что изменение состава и размера квантовой точки позволяет управлять активной средой такого лазера, стала возможна работа на длинах волн, которые раньше были недоступны.
Эта технология активно применяется на практике в медицине, с ее помощью был создан лазерный скальпель.
Рис. 9 - Схема лазера на квантовых точках

МОДЕЛЬ МНОГОБАРЬЕРНОЙ ПОТЕНЦИАЛЬНОЙ СТРУКТУРЫ
18
Рис. 11 – Энергетическая диаграмма четырехбарьерной симметричной структуры
Нам требуется построить модель четырёхбарьерной потенциальной структуры с симметричными барьерами шириной L1 и высотой U1 и одинаковым расстоянием между барьерами L2.

МОДЕЛЬ МНОГОБАРЬЕРНОЙ ПОТЕНЦИАЛЬНОЙ СТРУКТУРЫ
19
Для построения модели решим одномерное уравнение Шрёдингера для данного случая и найдём коэффициенты пропускания Т и отражения R.
Запишем общий вид одномерного уравнения Шрёдингера:
где H0 — гамильтониан электрона для стационарной задачи,

МОДЕЛЬ МНОГОБАРЬЕРНОЙ ПОТЕНЦИАЛЬНОЙ СТРУКТУРЫ
20
Нас же интересует стационарная задача. Запишем отсюда стационарное уравнение Шрёдингера:
Решение будем искать в виде:

МОДЕЛЬ МНОГОБАРЬЕРНОЙ ПОТЕНЦИАЛЬНОЙ СТРУКТУРЫ
21
где волновые числа:
Коэффициенты B (0) , B (8) , B (p) , B (p) P = 1..7 можно найти из условий равенства волновых функций и плотностей их потоков на всех границах наносистемы:

МОДЕЛЬ МНОГОБАРЬЕРНОЙ ПОТЕНЦИАЛЬНОЙ СТРУКТУРЫ
22
при условии нормировки:
При нахождении всех коэффициентов можно найти плотность тока:

ЗАКЛЮЧЕНИЕ
22
По результатам данной курсовой работы нами успешно освоены основные модели одномерных и нульмерных потенциальных структур (потенциальная ступень, квантовая яма, потенциальный барьер, квантовая точка), изучены методы изготовления потенциальных структур. Кроме того, мы ознакомились с текущим состоянием развития наноэлектроники и новыми разработками наноэлектронных приборов и устройств, получили сведения об основных сценариях применения различных потенциальных структур.