Содержание
- 2. Введение Программируемые сопротивления 3. Теорема минимальной реализации программно-управляемых сопротивлений 4. Четыре схемы программируемых сопротивлений 5. Минимальная
- 3. Лекция 9 Введение Современные приборы для измерений зачастую имеют модульную конструкцию. Каждый модуль состоит из большого
- 4. Лекция 9 Под минимальной реализацией будем понимать использование наименьшего числа компонентов. Теорема: Для минимальной реализации набора
- 5. Лекция 9 Минимальная реализация программно-управляемых сопротивлений Под минимальной реализацией будем понимать использование наименьшего числа компонентов. Теорема:
- 6. Лекция 9 Рассмотрим два типа операций переключения. Режим одиночного переключения: В момент Н все ключи разомкнуты
- 7. Лекция 9 1. Режим одиночного переключения Для реализации всех N значений параметра С, соответствующих k =
- 8. Лекция 9 2. Режим группового переключения В момент Н группа ключей S1, S2,..., Sk замкнута (разомкнута),
- 9. Лекция 9 2. Режим группового переключения Для реализации всех N значений Сk соответствующих k = 1,
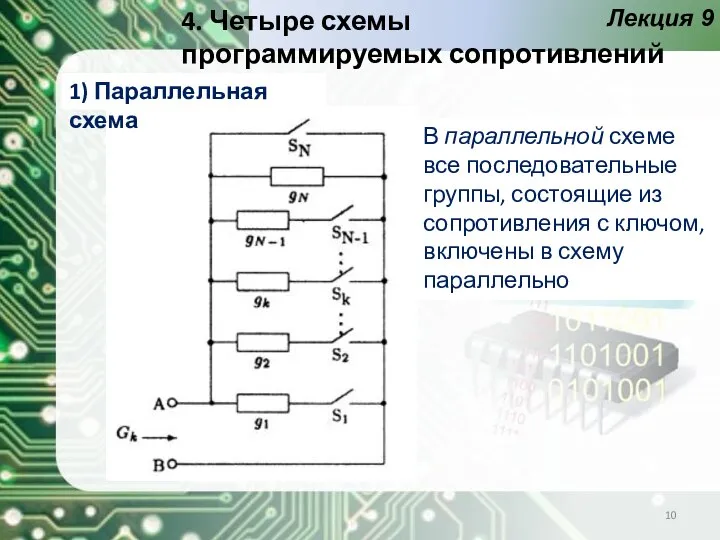
- 10. Лекция 9 4. Четыре схемы программируемых сопротивлений В параллельной схеме все последовательные группы, состоящие из сопротивления
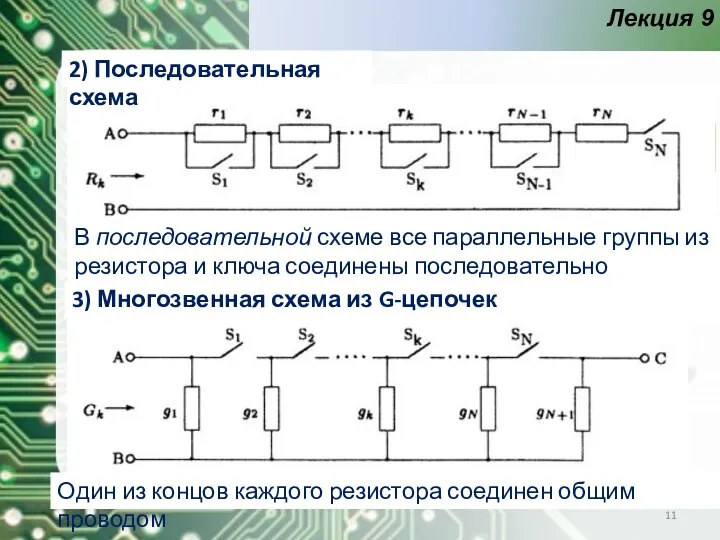
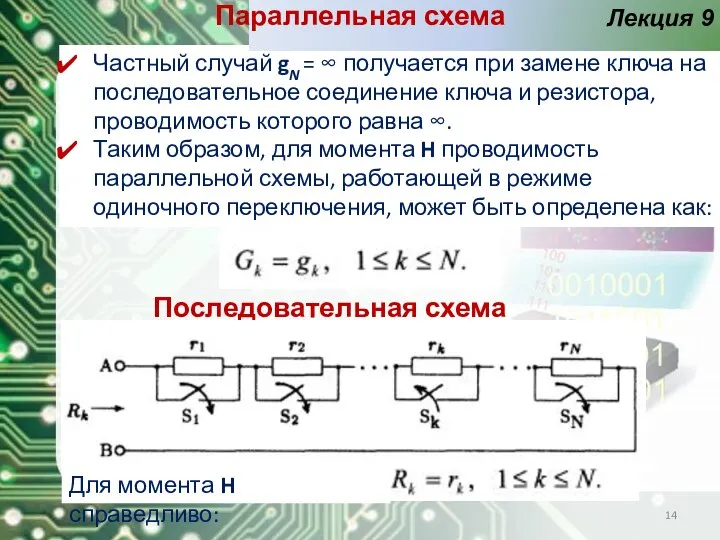
- 11. Лекция 9 2) Последовательная схема В последовательной схеме все параллельные группы из резистора и ключа соединены
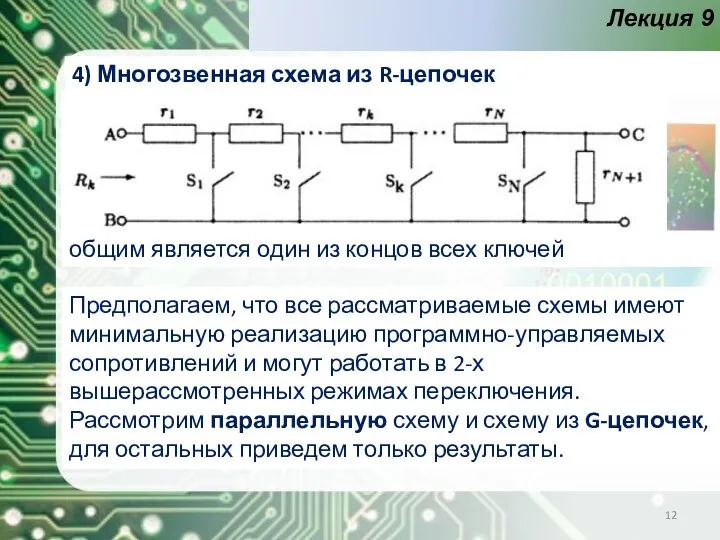
- 12. Лекция 9 4) Многозвенная схема из R-цепочек общим является один из концов всех ключей Предполагаем, что
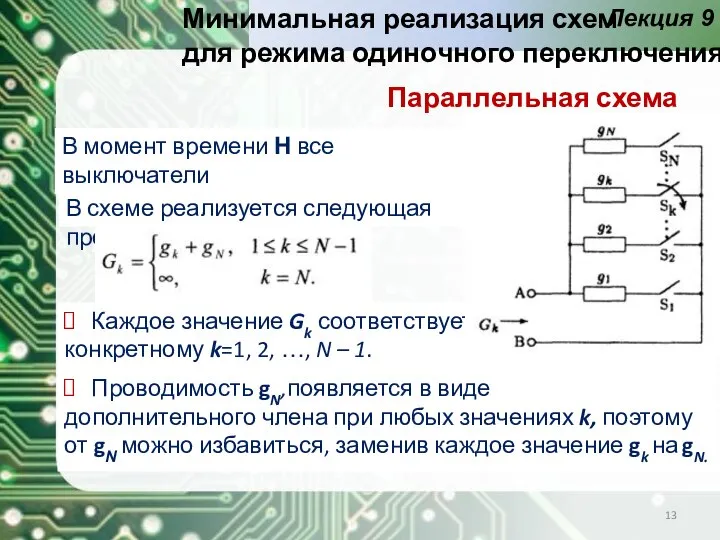
- 13. Каждое значение Gk соответствует конкретному k=1, 2, …, N – 1. Проводимость gN,появляется в виде дополнительного
- 14. Частный случай gN = ∞ получается при замене ключа на последовательное соединение ключа и резистора, проводимость
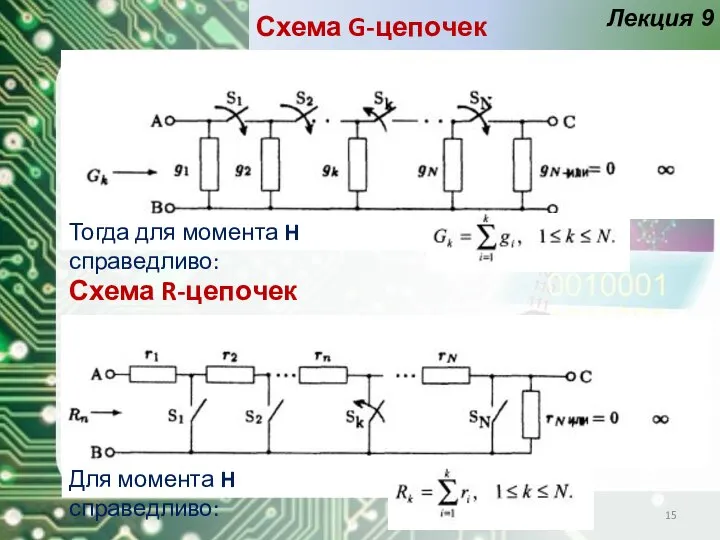
- 15. Лекция 9 Схема G-цепочек Схема R-цепочек Тогда для момента H справедливо: Для момента H справедливо:
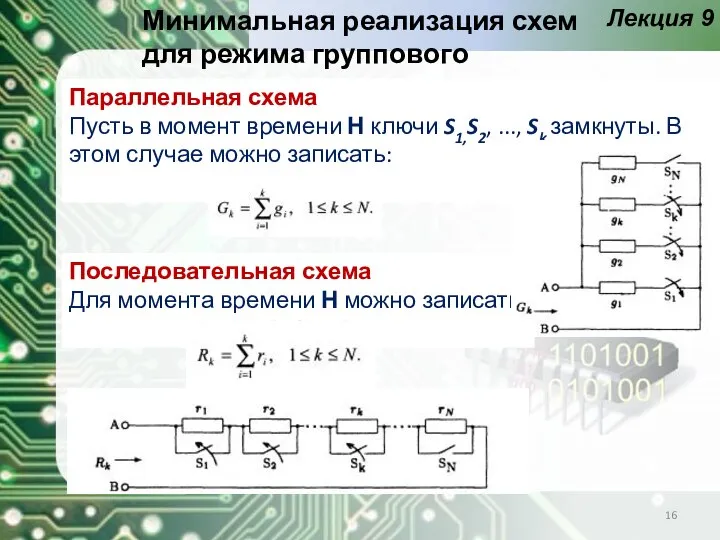
- 16. Лекция 9 Минимальная реализация схем для режима группового переключения Параллельная схема Пусть в момент времени Н
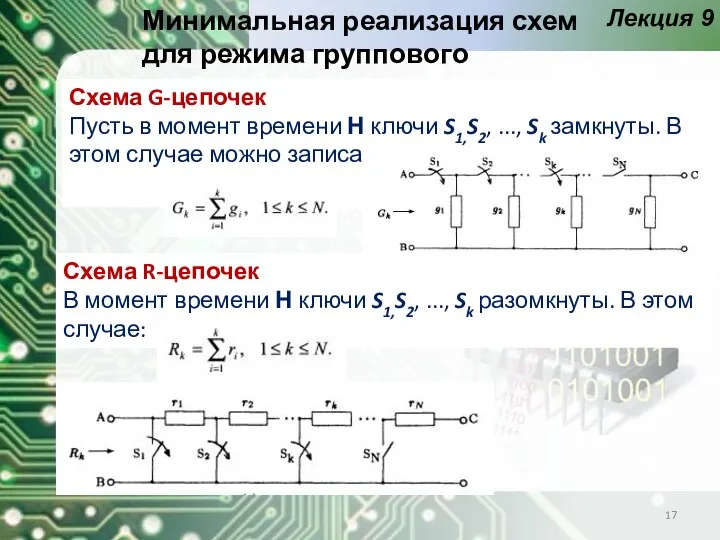
- 17. Лекция 9 Минимальная реализация схем для режима группового переключения Схема G-цепочек Пусть в момент времени Н
- 18. 2) Схема G-цепочек А. Режим одиночного переключения Параллельное / последовательное соединение Лекция 9 Расчет программируемых сопротивлений
- 19. 2) Последовательное соединение / Схема R-цепочек Б. Режим группового переключения Параллельное соединение/ Схема G-цепочек Лекция 9
- 20. Количество используемых резисторов будет уменьшаться на единицу для каждого последующего значения сопротивления (проводимости), изменяющегося от 0
- 21. Как при одиночном, так и при групповом режиме переключения требуется преобразование двоичного кода в код, пригодный
- 22. Во всех параллельных схемах для компенсации сопротивления Rsk замкнутого ключа Sk можно уменьшить значение последовательного с
- 23. Лекция 9 Программируемые делители Если в многозвенной схеме на основе G-цепочек gN+1 = 0, то она
- 24. Лекция 9 Задание для самостоятельной работы Разработайте схемы для получения наборов сопротивлений: а) 0, 1, 2,
- 25. Лекция 9 Проверь себя! Вопрос 1 : Ответы: а)
- 26. Лекция 9 Проверь себя! Вопрос 2: … Ответы: а) действующее значение напряжения б) мгновенное в) среднее
- 27. Лекция 9 Проверь себя! Вопрос 3 : … Ответы: а)
- 28. Лекция 9 Проверь себя! Вопрос 4 : … Ответы: а)
- 29. Лекция 9 Проверь себя! Вопрос 5 : … Ответы: а) б) в) г) д)
- 31. Скачать презентацию
















 Анализ видов и кинематических параметров движений
Анализ видов и кинематических параметров движений Оценка одновременно нескольких параметров
Оценка одновременно нескольких параметров Нагревание проводников электрическим током
Нагревание проводников электрическим током Теоретические основы разработки полимерных композиционных материалов триботехнического назначения. Задание на КП
Теоретические основы разработки полимерных композиционных материалов триботехнического назначения. Задание на КП Резонанс. Учет и использование резонанса в быту и промышленности
Резонанс. Учет и использование резонанса в быту и промышленности Изображения, даваемые линзой
Изображения, даваемые линзой Выращивание кристаллов Учитель физики МОУ «Тюбукская СОШ №3» Каслинского муниц
Выращивание кристаллов Учитель физики МОУ «Тюбукская СОШ №3» Каслинского муниц Измерительный прибор для определения влажности воздуха - гигрометр
Измерительный прибор для определения влажности воздуха - гигрометр Взаимодействие тел (1)
Взаимодействие тел (1) Солнце, воздух и вода – наши лучшие друзья
Солнце, воздух и вода – наши лучшие друзья Звездный колейдоскоп
Звездный колейдоскоп Ремонт клиновой и параллельной (двухдисковой) задвижки
Ремонт клиновой и параллельной (двухдисковой) задвижки Питание
Питание Учение об атоме. Квантовая теория строения атома
Учение об атоме. Квантовая теория строения атома Пример планового техобслуживания автомобиля
Пример планового техобслуживания автомобиля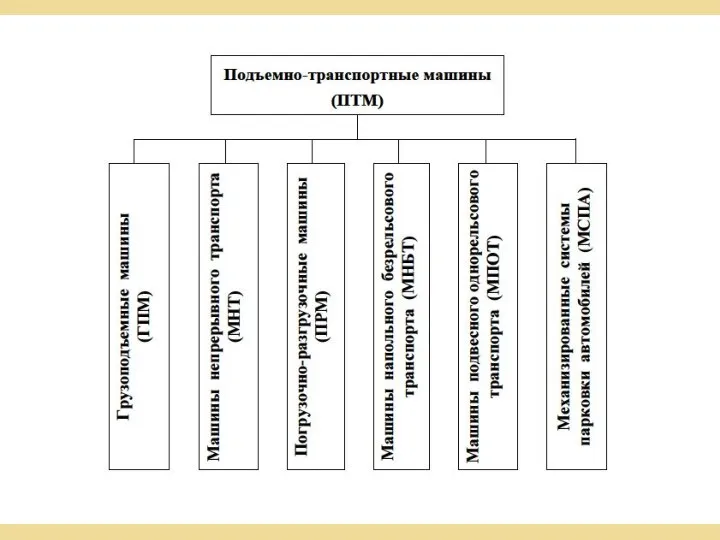 Классификация подъемно-транспортных машин
Классификация подъемно-транспортных машин 4-3 القوى المتوازنة والقوى غير المتوازنة
4-3 القوى المتوازنة والقوى غير المتوازنة Отраслевая олимпиада ПАО РусГидро по физике Энергия образования для школьников 7-11 классов
Отраслевая олимпиада ПАО РусГидро по физике Энергия образования для школьников 7-11 классов Свойства материалов
Свойства материалов Квантовые вычисления
Квантовые вычисления Преобразования сигналов и Вейвлет-преобразование
Преобразования сигналов и Вейвлет-преобразование Электроэнергетические системы и сети. Определение параметров элементов электрической сети
Электроэнергетические системы и сети. Определение параметров элементов электрической сети Движение тела по окружности с постоянной по модулю скоростью
Движение тела по окружности с постоянной по модулю скоростью Безопасность дорожного движения и особенности управления
Безопасность дорожного движения и особенности управления Тормозные системы
Тормозные системы Метрология
Метрология Тайны и чудеса зимушки-зимы
Тайны и чудеса зимушки-зимы Фотоэффект. Самостоятельная работа
Фотоэффект. Самостоятельная работа