Содержание
- 2. Расчет объектива - монохромата Объектив – монохромат применяют в интерферометрах для создания эталонного сферического волнового фронта.
- 3. Расчет объектива - монохромата Параметры 1-го вспомогательного луча Поверхностные коэффициенты Радиусы кривизны поверхностей Сумма Зейделя Зиновьев
- 4. Расчет двухлинзового склеенного объектива Переменными параметрами могут являться: - радиусы (3 шт.), - толщины (2 шт.),
- 5. Расчет двухлинзового склеенного объектива Условия нормировки Принимая толщины равными 0, имеем: Приведенная первая хроматическая сумма В
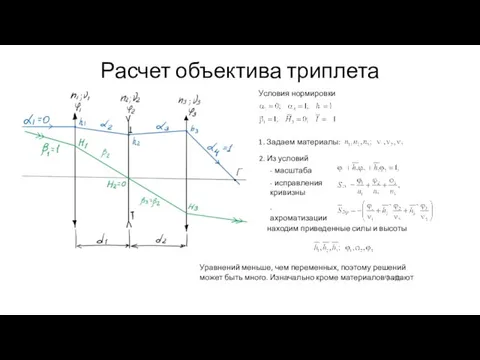
- 6. Расчет объектива триплета Условия нормировки 1. Задаем материалы: 2. Из условий - масштаба - исправления кривизны
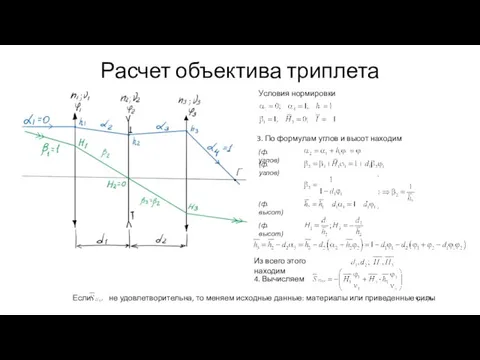
- 7. Расчет объектива триплета Условия нормировки 3. По формулам углов и высот находим (ф. углов) (ф. высот)
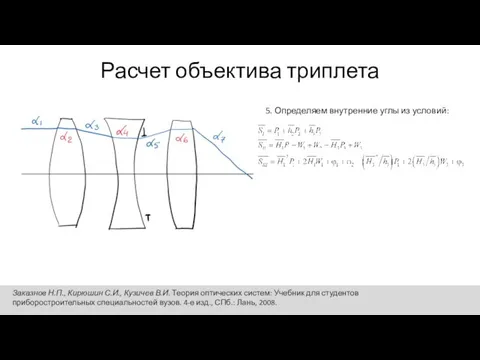
- 8. Расчет объектива триплета 5. Определяем внутренние углы из условий: Заказнов Н.П., Кирюшин С.И., Кузичев В.И. Теория
- 9. Некоторые оптические элементы с особыми аберрационными свойствами
- 10. Апланатические поверхности Сферическая аберрация III порядка отсутствует, если Из геометрических соображений Закон преломления Для апланатической поверхности
- 11. Апланатические поверхности Для апланатической поверхности 2-го рода Для апланатической поверхности 3-го рода
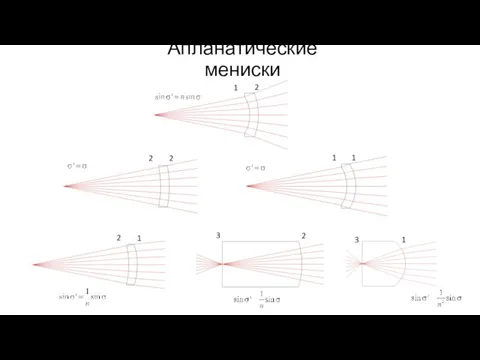
- 12. Апланатические мениски 1 2 2 2 1 2 1 1 1 3 3 2
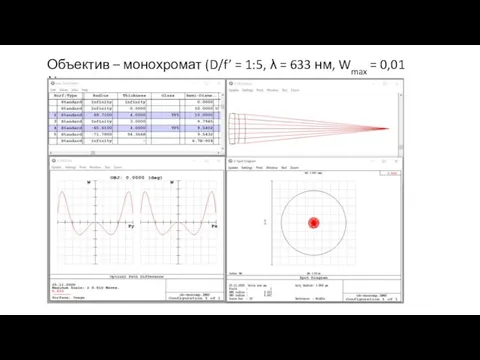
- 13. Объектив – монохромат (D/f’ = 1:5, λ = 633 нм, Wmax = 0,01 λ)
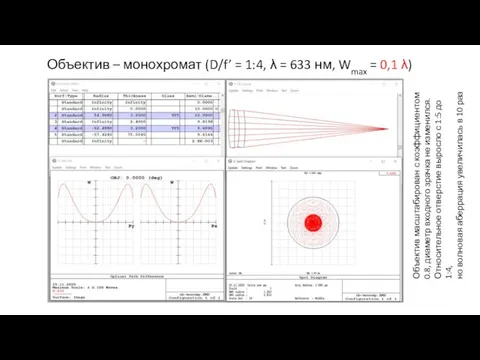
- 14. Объектив – монохромат (D/f’ = 1:4, λ = 633 нм, Wmax = 0,1 λ) Объектив масштабирован
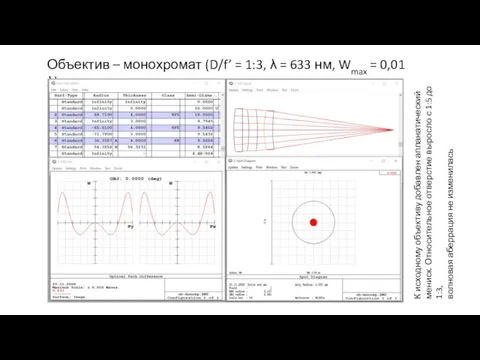
- 15. Объектив – монохромат (D/f’ = 1:3, λ = 633 нм, Wmax = 0,01 λ) К исходному
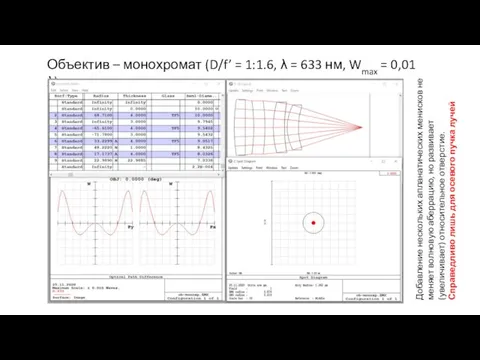
- 16. Объектив – монохромат (D/f’ = 1:1.6, λ = 633 нм, Wmax = 0,01 λ) Добавление нескольких
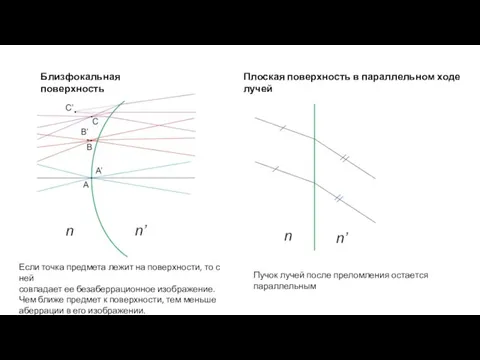
- 17. Поверхность, концентричная зрачку Главный луч проходит через центр кривизны С и совпадает с осью симметрии сферической
- 18. Плоская поверхность в параллельном ходе лучей Пучок лучей после преломления остается параллельным Близфокальная поверхность Если точка
- 19. Оптическая система представляется в виде композиции базовых (силовых) и коррекционных компонентов. Комбинируя следующие поверхности: - апланатические
- 20. Примеры базовых линз Б(ок) Б(ка)
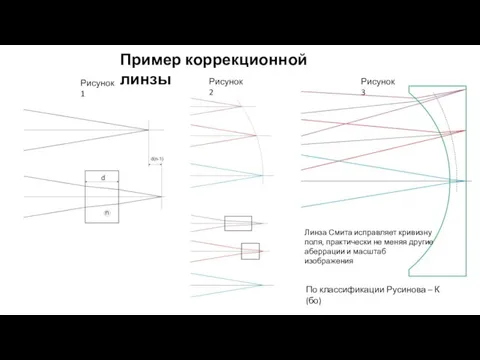
- 21. Пример коррекционной линзы Линза Смита исправляет кривизну поля, практически не меняя другие аберрации и масштаб изображения
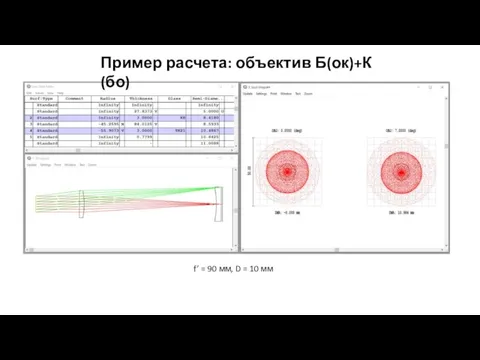
- 22. Пример расчета: объектив Б(ок)+К(бо) f’ = 90 мм, D = 10 мм
- 23. Зеркальные оптические системы
- 24. Микрообъективы Фотообъективы Астрономические объективы Оптические системы космических и наземных телескопов 1 2 3 4
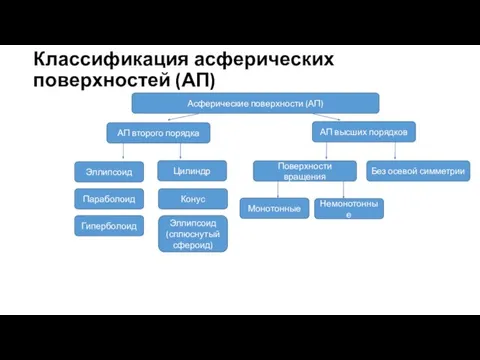
- 25. Классификация асферических поверхностей (АП) Асферические поверхности (АП) АП второго порядка АП высших порядков Эллипсоид Параболоид Гиперболоид
- 26. Меридиональный профиль АП Уравнения поверхностей вращения r0 – радиус при вершине, е - эксцентриситет 1 2
- 27. Свойства АП второго порядка 1. e2 2. e2 = 0 – сфера 3. 0 4. e2
- 28. Свойства АП второго порядка. Эллипсоид Эллипсоид – геометрическое место точек, сумма расстояний от которых до геометрических
- 29. Свойства АП второго порядка. Параболоид директрисса - геометрический фокус Парабола – геометрическое место точек, равноудаленных от
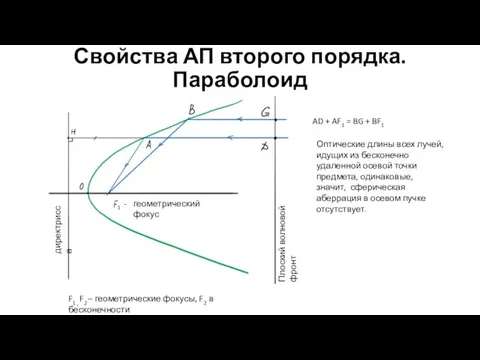
- 30. Свойства АП второго порядка. Параболоид директрисса Плоский волновой фронт геометрический фокус AD + AF1 = BG
- 31. Свойства АП второго порядка. Гиперболоид Эллипсоид – геометрическое место точек, разность расстояний от которых до геометрических
- 32. Отражающие асферические поверхности, образованные вращением кривой второго порядка вокруг оси, соединяющей их геометрические фокусы, имеют замечательное
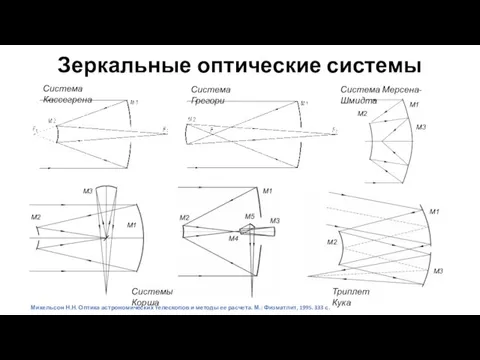
- 33. Зеркальные оптические системы М1 М3 М2 М3 Системы Корша Система Грегори М1 М2 Система Кассегрена Триплет
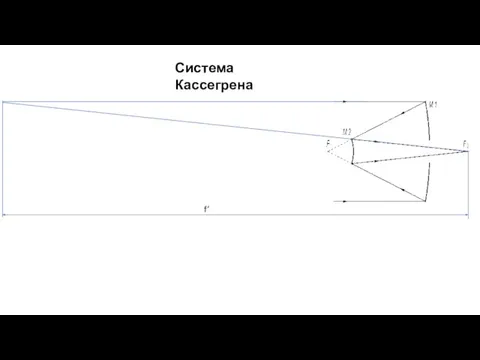
- 34. Система Кассегрена Телескоп БТА
- 35. Система Кассегрена f’
- 36. Система Кассегрена М1 – параболоид М2 – гиперболоид Отсутствуют только аберрации осевого пучка лучей и хроматические
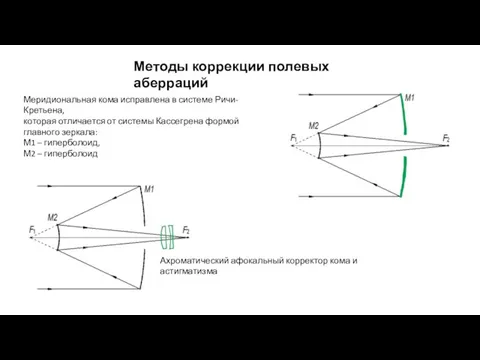
- 37. Меридиональная кома исправлена в системе Ричи-Кретьена, которая отличается от системы Кассегрена формой главного зеркала: М1 –
- 39. Скачать презентацию



















 Плоская задача теории упругости
Плоская задача теории упругости Аккумулирование энергии
Аккумулирование энергии Конструкция реактора РБМК–1000
Конструкция реактора РБМК–1000 Действие жидкости и газа на погружённое в них тело. Урок физики в 7 классе
Действие жидкости и газа на погружённое в них тело. Урок физики в 7 классе Аксиомы статики
Аксиомы статики Цифровые измерительные приборы. Мультиметр
Цифровые измерительные приборы. Мультиметр Презентация на тему Кристаллические и аморфные тела
Презентация на тему Кристаллические и аморфные тела 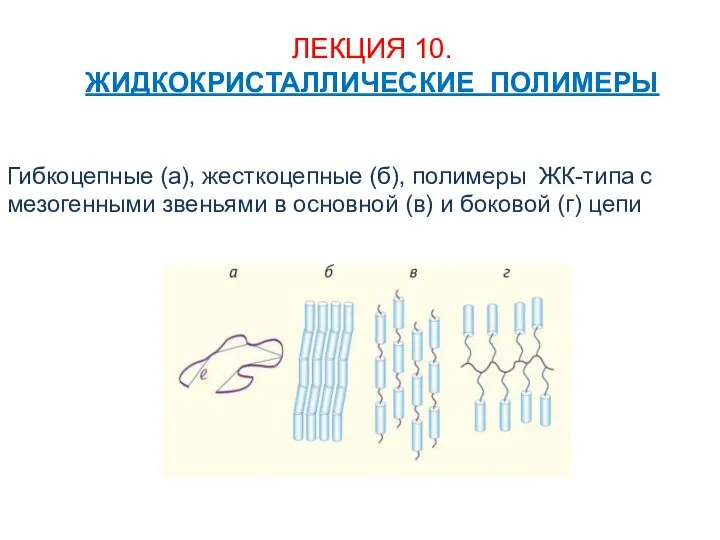 Жидкокристаллические полимеры
Жидкокристаллические полимеры Испарение и конденсация. Поглощение и выделение энергии
Испарение и конденсация. Поглощение и выделение энергии Источники света
Источники света Составные части комплекта виброизмерительной аппаратуры
Составные части комплекта виброизмерительной аппаратуры Большой адронный коллайдер
Большой адронный коллайдер Топ5 самых перспективных разработок атомной отрасли (Команда МОУ Лицей №1 10 класс)
Топ5 самых перспективных разработок атомной отрасли (Команда МОУ Лицей №1 10 класс) Электростатическое поле в диэлектрике. Лекция 3-2020
Электростатическое поле в диэлектрике. Лекция 3-2020 Строение атома
Строение атома Материалы, применяемые в электронике, электротехнике и радиотехнике
Материалы, применяемые в электронике, электротехнике и радиотехнике Презентация на тему Основные физические величины системы СИ
Презентация на тему Основные физические величины системы СИ  Взаимодействие тел. Масса
Взаимодействие тел. Масса Нанотехнологии в производстве изделий электронной техники
Нанотехнологии в производстве изделий электронной техники Электричество и магнетизм. Лекция 01. Электростатическое поле в вакууме
Электричество и магнетизм. Лекция 01. Электростатическое поле в вакууме Квазистационарное электромагнитное поле
Квазистационарное электромагнитное поле ДЕЛЕНИЕ И СИНТЕЗ ЯДЕР
ДЕЛЕНИЕ И СИНТЕЗ ЯДЕР Зубчатый механизм
Зубчатый механизм Виды конических зубчатых колес
Виды конических зубчатых колес Кафедра общей и прикладной геофизики
Кафедра общей и прикладной геофизики Шлифовальные станки
Шлифовальные станки Температура и тепловое равновесие
Температура и тепловое равновесие Электроосветительные приборы
Электроосветительные приборы