Содержание
- 2. Тема 6
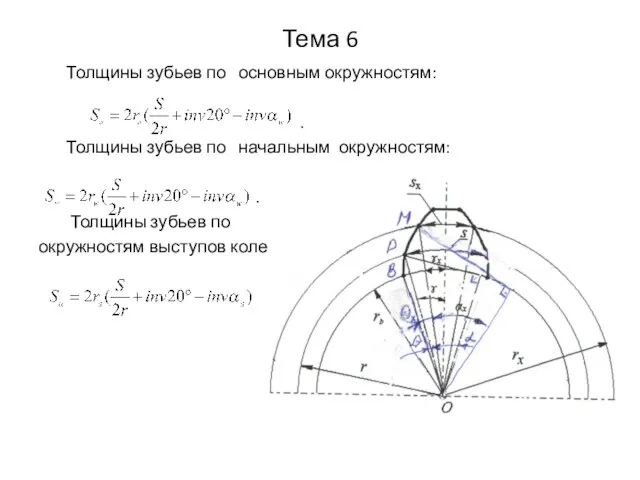
- 3. Тема 6 Толщины зубьев по основным окружностям: . Толщины зубьев по начальным окружностям: . Толщины зубьев
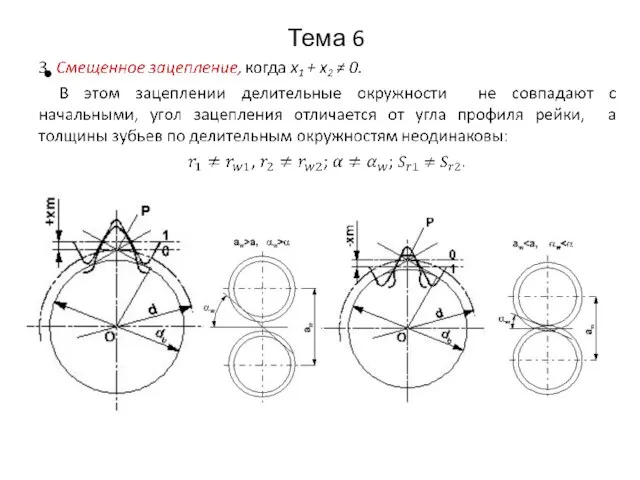
- 4. Тема 6 6.2.8. Определение угла зацепления Нарезанные с любыми коэффициентами смещения зубчатые колеса образуют эвольвентное зацепление
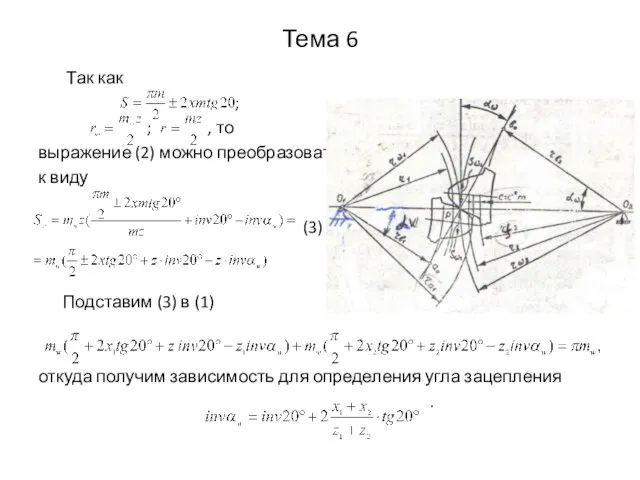
- 5. Тема 6 Так как ; ; , то выражение (2) можно преобразовать к виду (3) Подставим
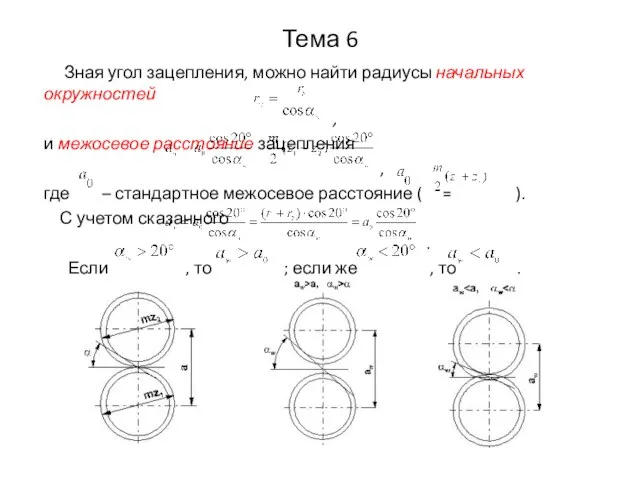
- 6. Тема 6 Зная угол зацепления, можно найти радиусы начальных окружностей , и межосевое расстояние зацепления ,
- 7. Тема 6 6.2.9. Определение радиусов окружностей впадин и выступов Радиусы окружностей впадин вычисляются по формуле .
- 8. Тема 6
- 9. Тема 6
- 10. Тема 6
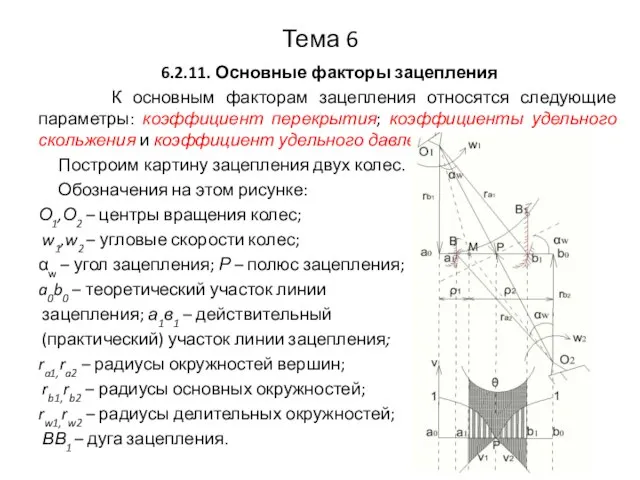
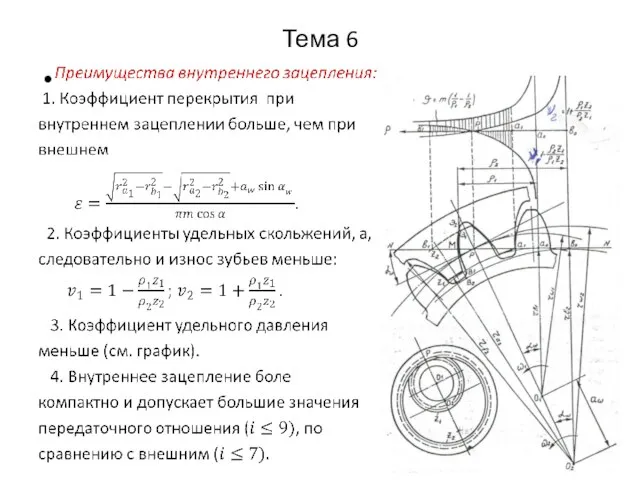
- 11. Тема 6 6.2.11. Основные факторы зацепления К основным факторам зацепления относятся следующие параметры: коэффициент перекрытия; коэффициенты
- 12. Тема 6
- 13. Тема 6
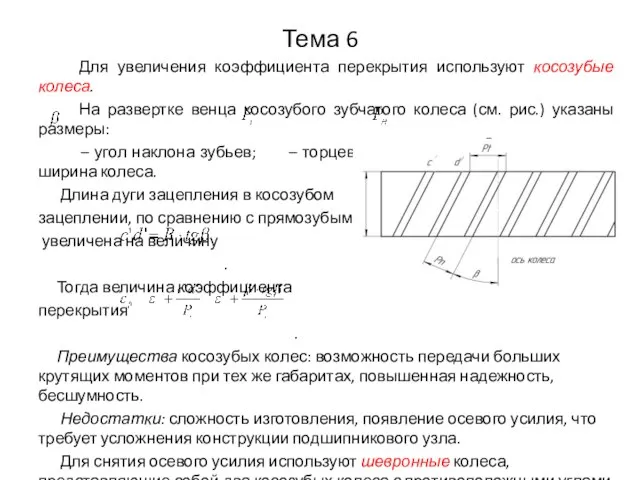
- 14. Тема 6 Для увеличения коэффициента перекрытия используют косозубые колеса. На развертке венца косозубого зубчатого колеса (см.
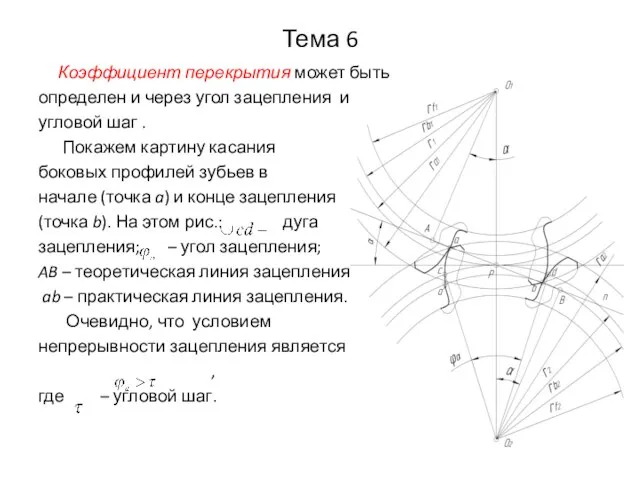
- 15. Тема 6 Коэффициент перекрытия может быть определен и через угол зацепления и угловой шаг . Покажем
- 16. Тема 6 Коэффициент перекрытия найдется через отношение угла зацепления к угловому шагу . (1) Угол зацепления
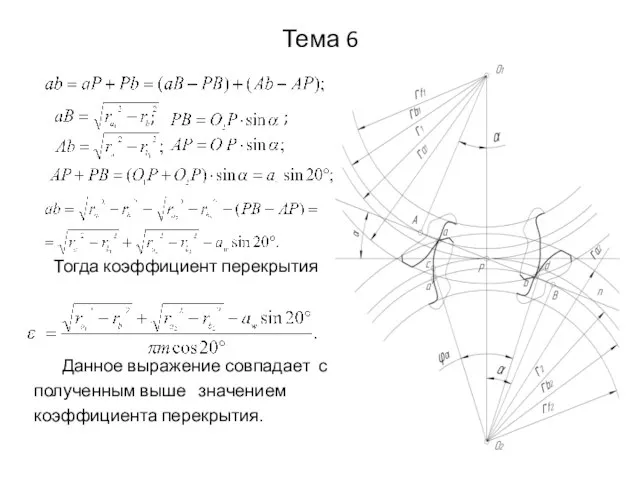
- 17. Тема 6 ; ; Тогда коэффициент перекрытия Данное выражение совпадает с полученным выше значением коэффициента перекрытия.
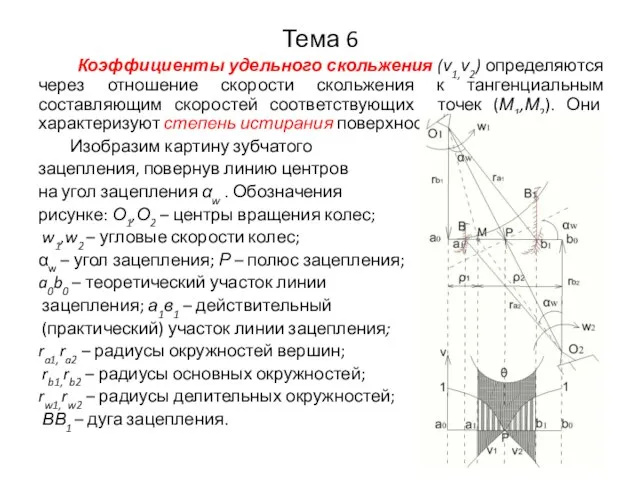
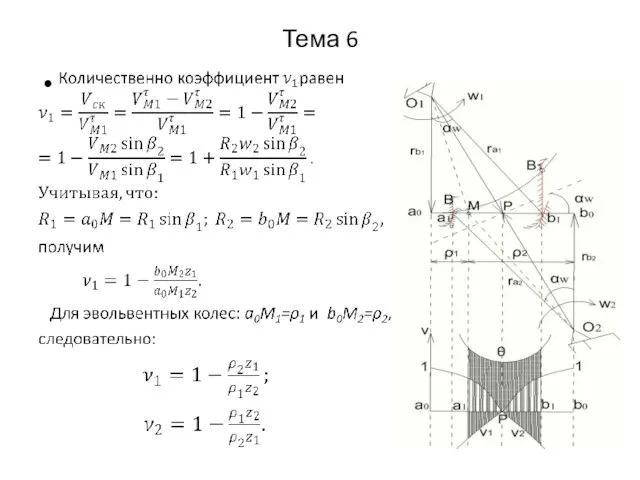
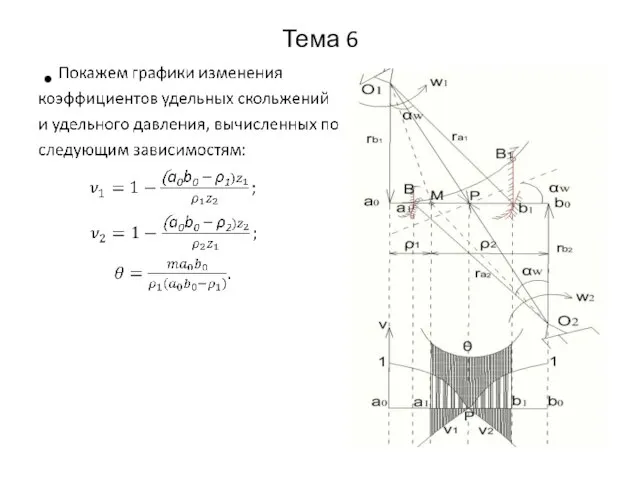
- 18. Тема 6 Коэффициенты удельного скольжения (ν1,ν2) определяются через отношение скорости скольжения к тангенциальным составляющим скоростей соответствующих
- 19. Тема 6
- 20. Тема 6
- 21. Тема 6
- 22. Тема 6 6.2.12. Цели смещения инструмента при изготовлении зубчатых колес (цели корригирования или исправления) Смещение инструмента
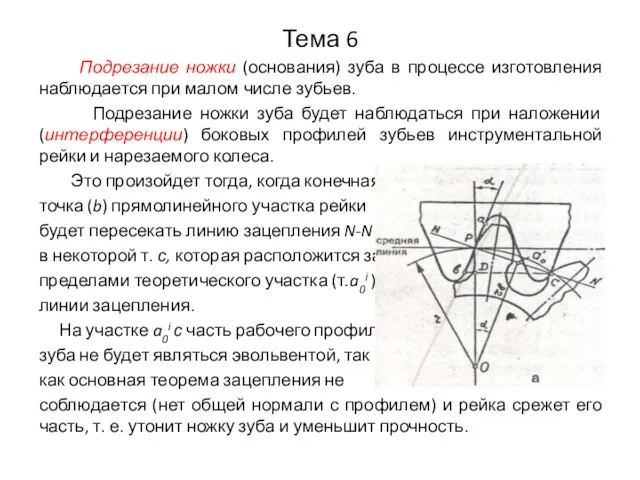
- 23. Тема 6 Подрезание ножки (основания) зуба в процессе изготовления наблюдается при малом числе зубьев. Подрезание ножки
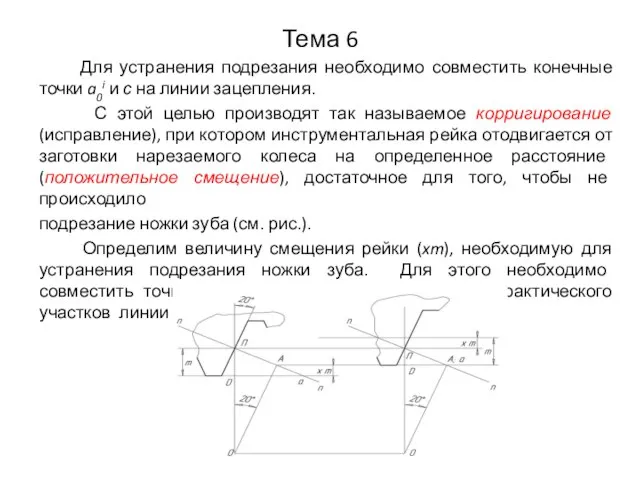
- 24. Тема 6 Для устранения подрезания необходимо совместить конечные точки a0i и с на линии зацепления. С
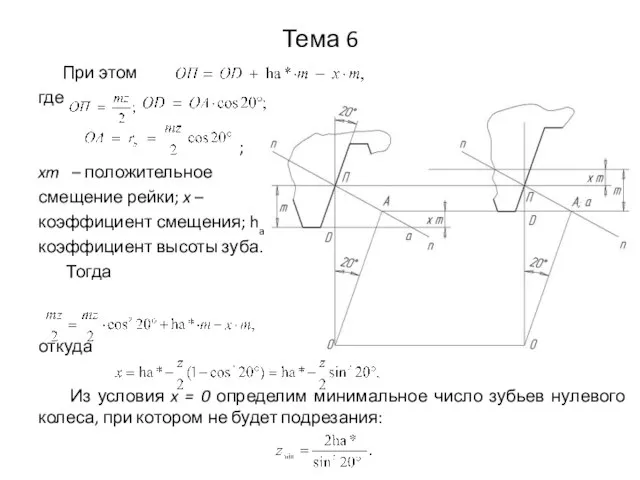
- 25. Тема 6 При этом где ; xm – положительное смещение рейки; x – коэффициент смещения; ha*
- 26. Тема 6 Для основного контура рейки ha*= 1, поэтому Для укороченного контура рейки (ha*= 0,8) минимальное
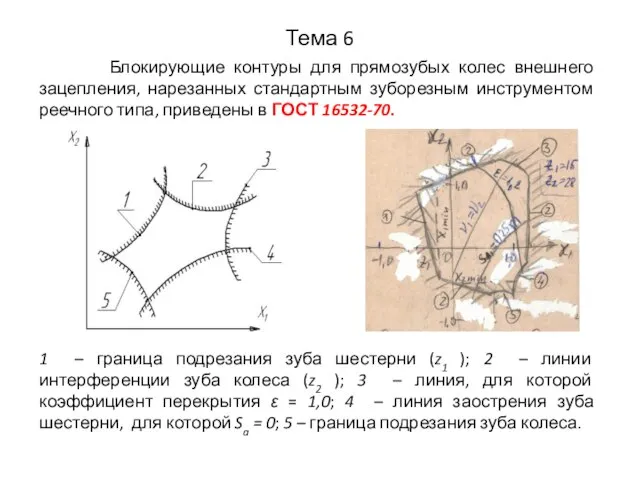
- 27. Тема 6 Блокирующие контуры для прямозубых колес внешнего зацепления, нарезанных стандартным зуборезным инструментом реечного типа, приведены
- 28. Тема 6
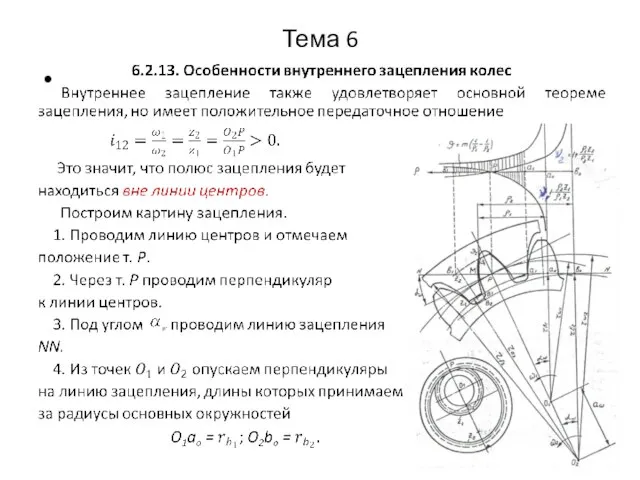
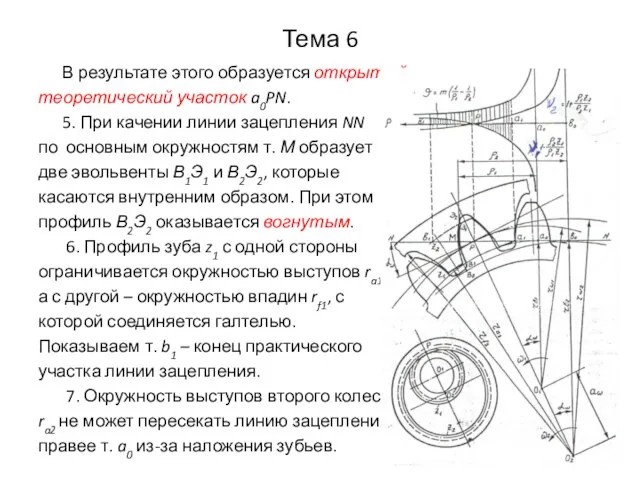
- 29. Тема 6 В результате этого образуется открытый теоретический участок a0PN. 5. При качении линии зацепления NN
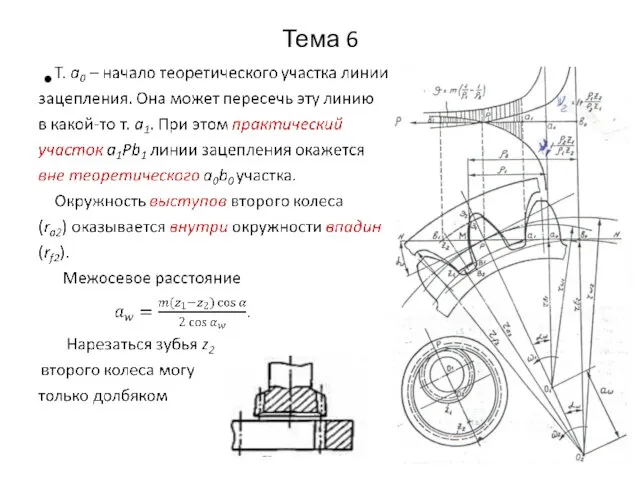
- 30. Тема 6
- 31. Тема 6
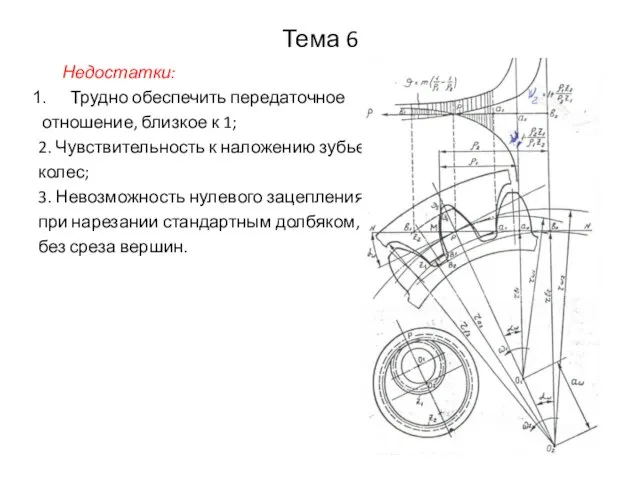
- 32. Тема 6 Недостатки: Трудно обеспечить передаточное отношение, близкое к 1; 2. Чувствительность к наложению зубьев колес;
- 33. Тема 6 6.2.14. Особенности конического зацепления Во многих машинах осуществление требуемых движений исполнительных механизмов связано с
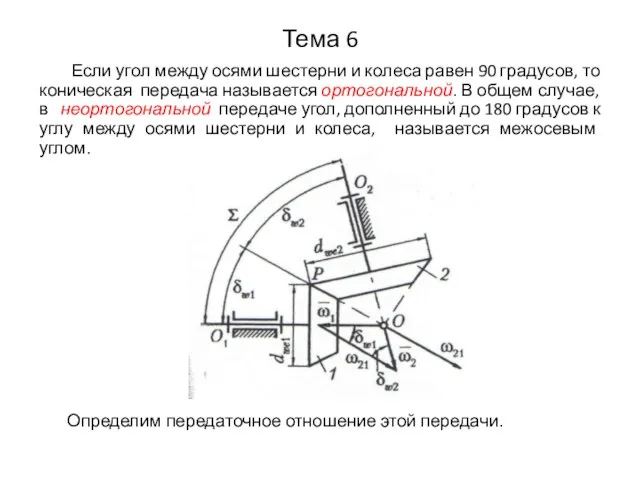
- 34. Тема 6 Если угол между осями шестерни и колеса равен 90 градусов, то коническая передача называется
- 35. Тема 6
- 36. Тема 6
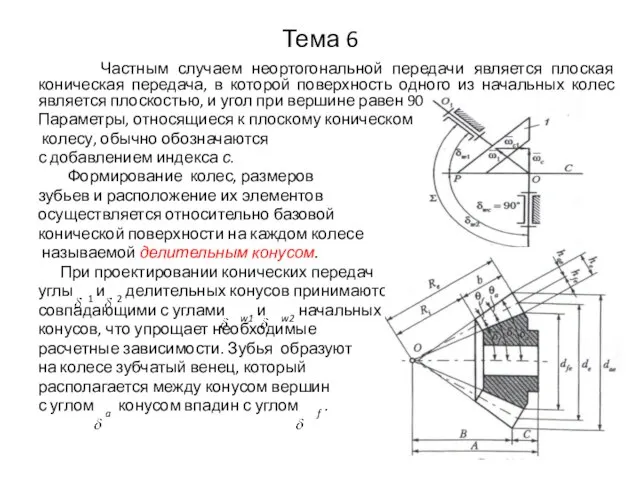
- 37. Тема 6 Частным случаем неортогональной передачи является плоская коническая передача, в которой поверхность одного из начальных
- 38. Тема 6
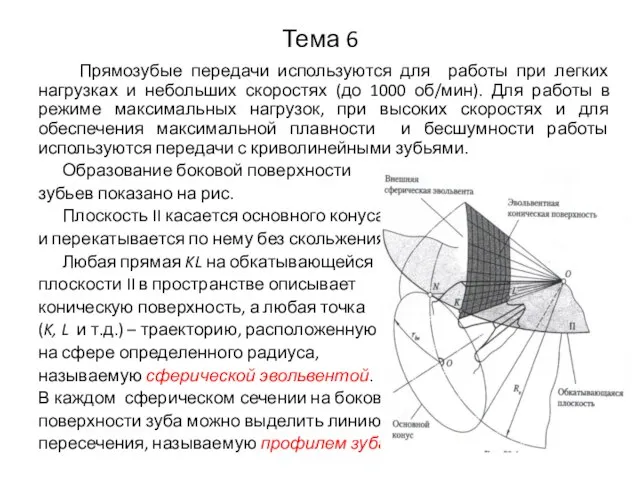
- 39. Тема 6 Прямозубые передачи используются для работы при легких нагрузках и небольших скоростях (до 1000 об/мин).
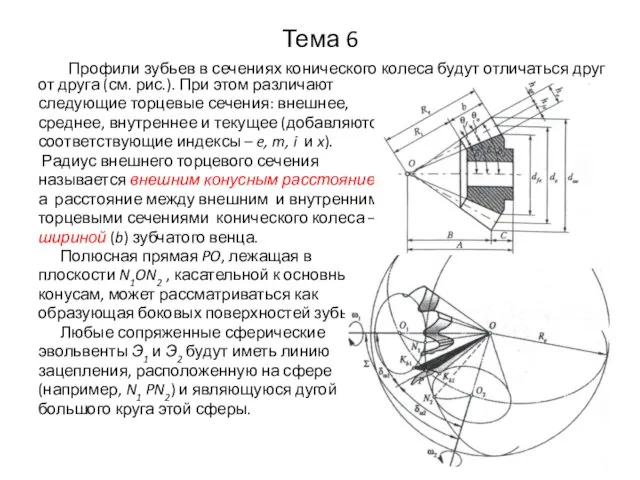
- 40. Тема 6 Профили зубьев в сечениях конического колеса будут отличаться друг от друга (см. рис.). При
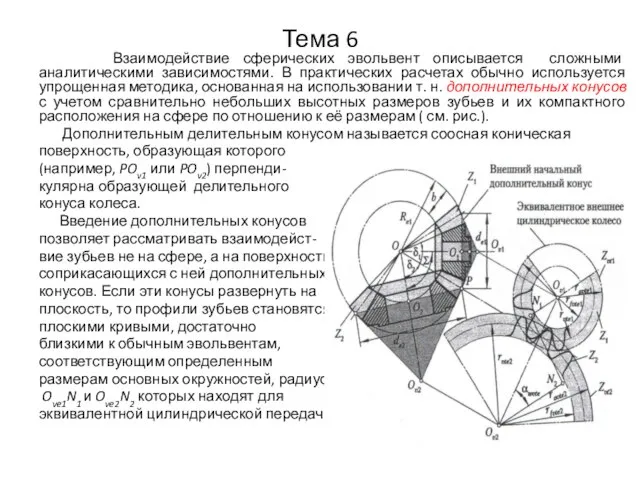
- 41. Тема 6 Взаимодействие сферических эвольвент описывается сложными аналитическими зависимостями. В практических расчетах обычно используется упрощенная методика,
- 42. Тема 6
- 43. Тема 6
- 45. Скачать презентацию

















 Переменный ток. Решение задач
Переменный ток. Решение задач Агрегатные состояния вещества
Агрегатные состояния вещества ГИА. Задачи, 2 часть
ГИА. Задачи, 2 часть Расчет смесителей
Расчет смесителей Центр тяжести.Виды равновесия (10 класс)
Центр тяжести.Виды равновесия (10 класс) Релаксация спинового ансамбля
Релаксация спинового ансамбля Физика – это наука о природе
Физика – это наука о природе Модель двигателя внешнего сгорания Стирлинга
Модель двигателя внешнего сгорания Стирлинга Урок по физике в 7 классе
Урок по физике в 7 классе Понятие устойчивости. Лекция 9
Понятие устойчивости. Лекция 9 Экспертные советы по теоретической физике
Экспертные советы по теоретической физике Электричество и магнетизм. Магнитные свойства вещества
Электричество и магнетизм. Магнитные свойства вещества Интерференция света. Дифракция света
Интерференция света. Дифракция света Сила тяжести
Сила тяжести Презентация на тему Свет и его законы
Презентация на тему Свет и его законы  Физика для химиков. День четвертый - электричество
Физика для химиков. День четвертый - электричество Лекция 1 Презентация Microsoft Office PowerPoint 2007
Лекция 1 Презентация Microsoft Office PowerPoint 2007 Импульс тела . Закон сохранения импульсов
Импульс тела . Закон сохранения импульсов Технічна механіка. Розрахунково-графічна робота С1
Технічна механіка. Розрахунково-графічна робота С1 Электромагнитные колебания и волны
Электромагнитные колебания и волны Естественная радиоактивность. Закон радиоактивного распада
Естественная радиоактивность. Закон радиоактивного распада ОМиУОИ_л1
ОМиУОИ_л1 Электрический ток в металлах
Электрический ток в металлах Измерение силы Архимеда
Измерение силы Архимеда Магнитное поле
Магнитное поле ВКР: Морозильное судно для перевозки скоропортящихся грузов
ВКР: Морозильное судно для перевозки скоропортящихся грузов Лекция 9. Выпаривание
Лекция 9. Выпаривание Решение задач с помощью законов Ньютона
Решение задач с помощью законов Ньютона