Разностноное уравнение и передаточная функция

Разностноное уравнение и передаточная функция
Сравнивая (3) и (4), находим, что
(5).
Комплексно-сопряженные корни
(6).

АЧХ цифрового фильтра
АЧХ нерекурсивного ЦФ
(11)

АЧХ цифрового фильтра
АЧХ и нуль-полюсная диаграмма НЦФ 2-го порядка.
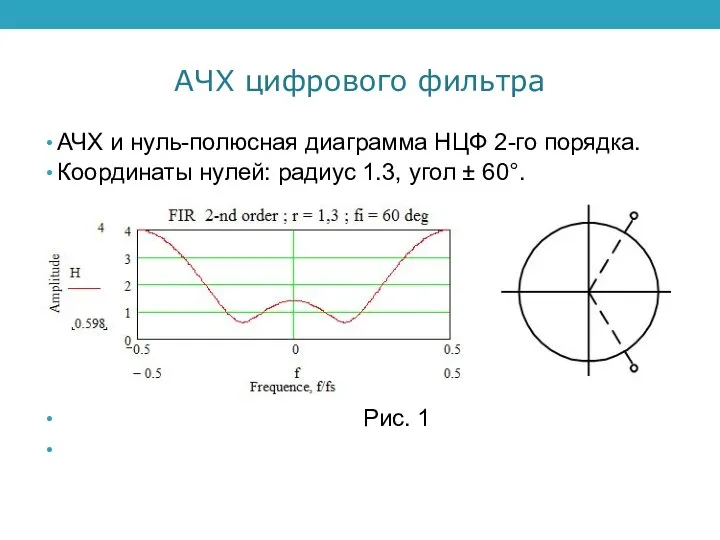
Координаты нулей: радиус 1.3, угол ± 60°.
Рис. 1

АЧХ цифрового фильтра
АЧХ и нуль-полюсная диаграмма НЦФ 2-го порядка.
Координаты нулей: радиус 1.0, угол ± 60°.
Рис. 2

АЧХ цифрового фильтра
АЧХ и нуль-полюсная диаграмма НЦФ 2-го порядка.
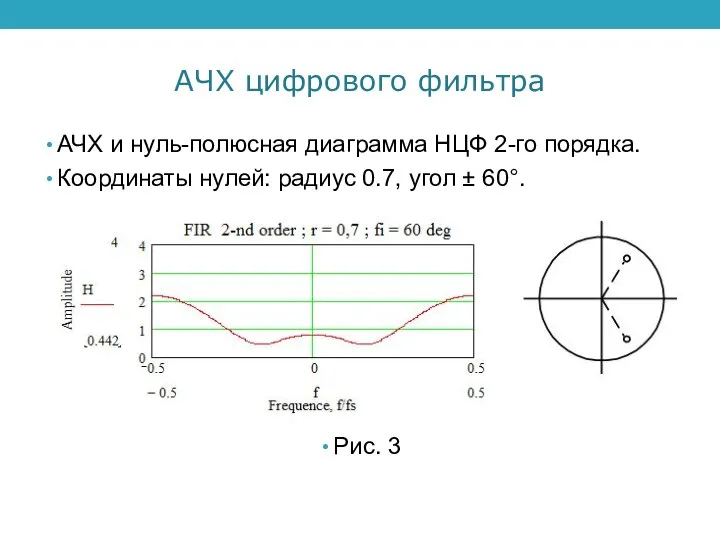
Координаты нулей: радиус 0.7, угол ± 60°.
Рис. 3

АЧХ цифрового фильтра
Для того, чтобы получить наибольшее затухание на частотах вблизи нулей передаточной функции, необходимо, чтобы нули лежали на единичной окружности, т.е. должно быть r = 1.
В этом случае a2 = 1, a1 = -2cosϕ, и АЧХ равна
(12).

АЧХ цифрового фильтра
Если в (3) подставить exp(jωT) вместо z и взять модуль, т.е. вычислить АЧХ, то получим

АЧХ цифрового фильтра
Так как модуль комплексной экспоненты равен единице, а модуль разности между текущей точкой exp(jωT) и положением нуля равен расстоянию между ними (см. рис 4), то значение АЧХ НЦФ на частоте ω равно произведению расстояний ρ0i от точки ejωT, лежащей на единичной окружности плоскости z, до всех нулей фильтра:
(13).

АЧХ цифрового фильтра
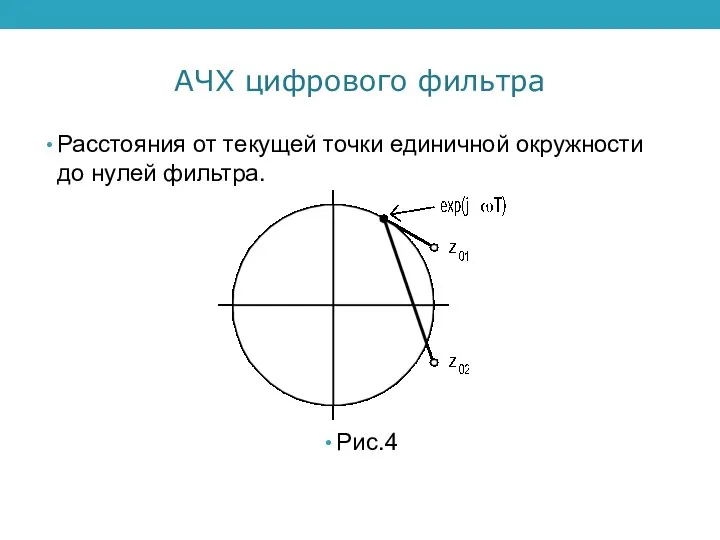
Расстояния от текущей точки единичной окружности до нулей фильтра.
Рис.4

АЧХ цифрового фильтра
Так как
то АЧХ НЦФ общего вида.
(14)