Содержание
- 2. Проводники и диэлектрики Диэлектрик – вещество, где нет свободных электрических зарядов, способных перемещаться под действием приложенного
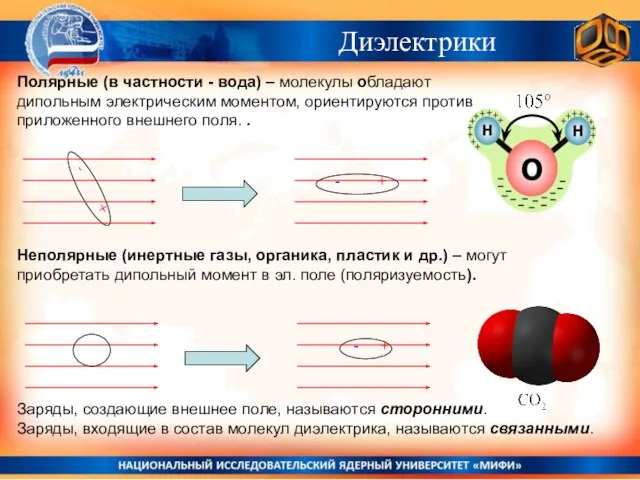
- 3. Полярные (в частности - вода) – молекулы обладают дипольным электрическим моментом, ориентируются против приложенного внешнего поля.
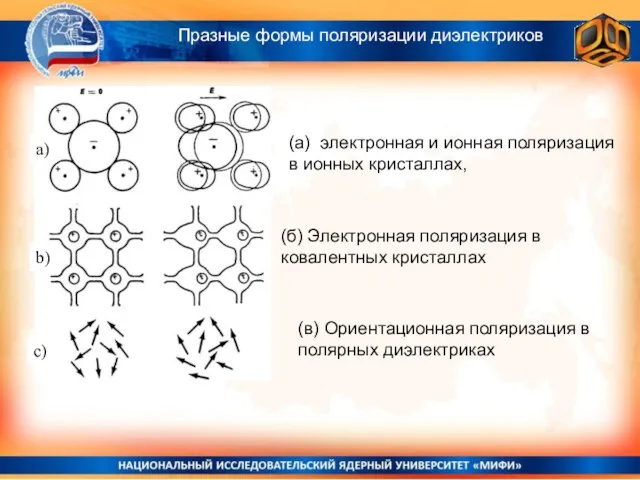
- 4. (а) электронная и ионная поляризация в ионных кристаллах, Празные формы поляризации диэлектриков (б) Электронная поляризация в
- 5. Поляризация диэлектриков Эффект поляризации – см. «Физика в опытах»!
- 6. Поляризация диэлектриков Вектор поляризованности – дипольный момент единицы объема поляризованного вещества ΣPi=0 ΣPi=0 / ΔV Опыт:
- 7. Характеристики диэлектриков Вектор поляризованности – дипольный момент единицы объема поляризованного вещества В изотропном диэлектрике P =
- 8. Теорема Гаусса для поляризованности +σ -σ h n -n P dS |Σp| = hσdS = PdV
- 9. Теорема Гаусса для поляризованности σ = (P,n) n ds P S, V QS= ∫ σds =
- 10. Электрическая индукция (смещение)
- 11. Уравнение электростатического поля В изотропном диэлектрике div D = ρ = ε0ε div E = ε0ε
- 12. Теорема Гаусса для вектора электрического смещения в интегральной форме Аналогия с теоремой Гаусса для электрического поля.
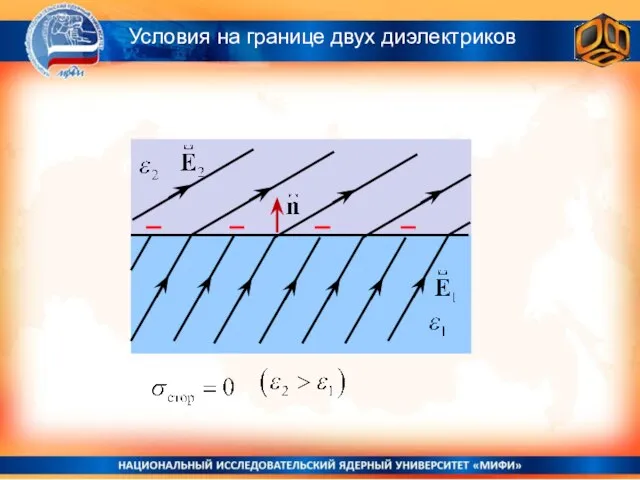
- 13. Поверхностная плотность связанных зарядов на границе двух диэлектриков Условия на границе двух диэлектриков σ = (P,n)
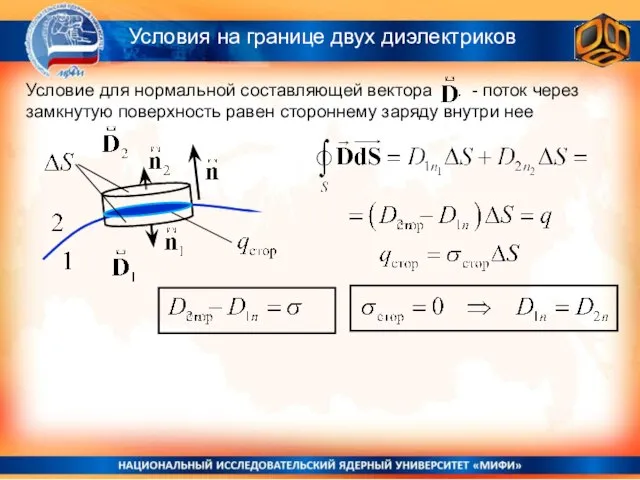
- 14. Условия на границе двух диэлектриков
- 15. Условия на границе двух диэлектриков
- 16. Условия на границе двух диэлектриков E1 , D1 E2 , D2
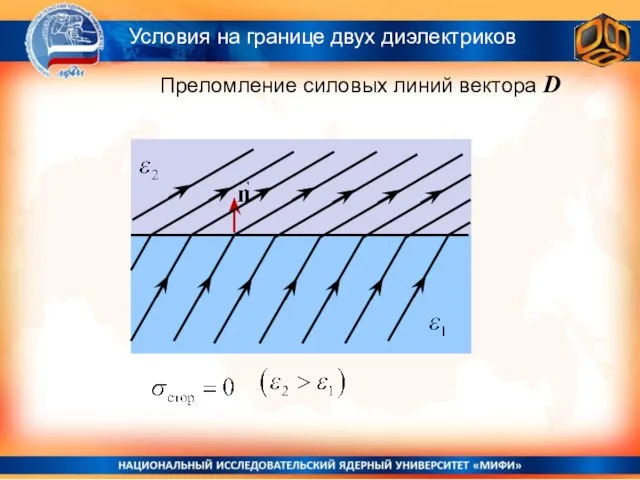
- 17. tg a1/tga2 = D1tD2n/D1nD2t Условия на границе двух диэлектриков Преломление силовых линий вектора D
- 18. Условия на границе двух диэлектриков Преломление силовых линий вектора D
- 19. Условия на границе двух диэлектриков
- 20. Условия на границе двух диэлектриков
- 21. Условия на границе двух диэлектриков
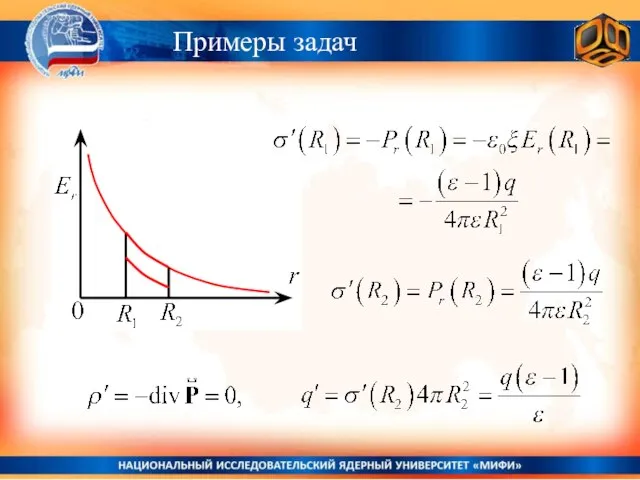
- 22. Примеры задач Пример 1
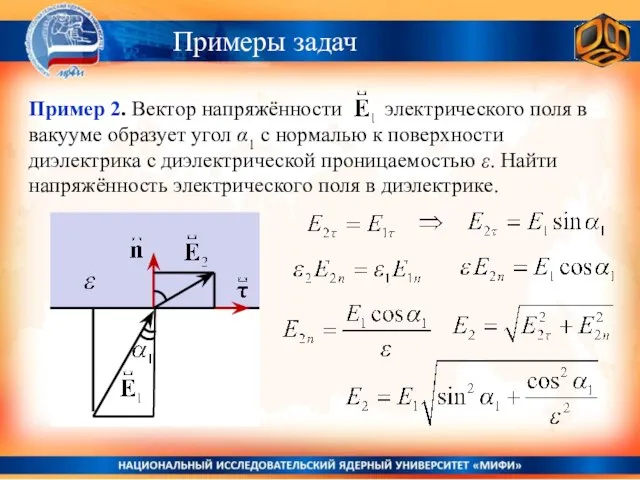
- 23. Примеры задач
- 24. Примеры задач
- 25. Пример загадки Пример 3. И2.44 Определить напряженность поля Е, если его потенциал А) φ = a(x2+y2)
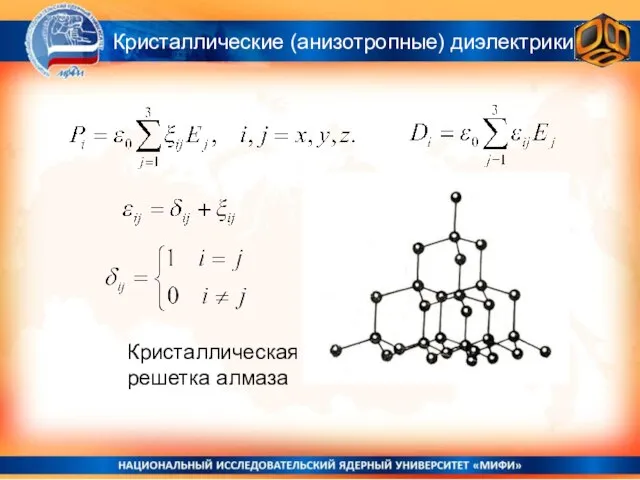
- 26. Кристаллические (анизотропные) диэлектрики Кристаллическая решетка алмаза
- 27. Кристаллические диэлектрики Пьезоэлектрики – кристаллические диэлектрики, в которых при сжатии и растяжении в определённых направлениях возникает
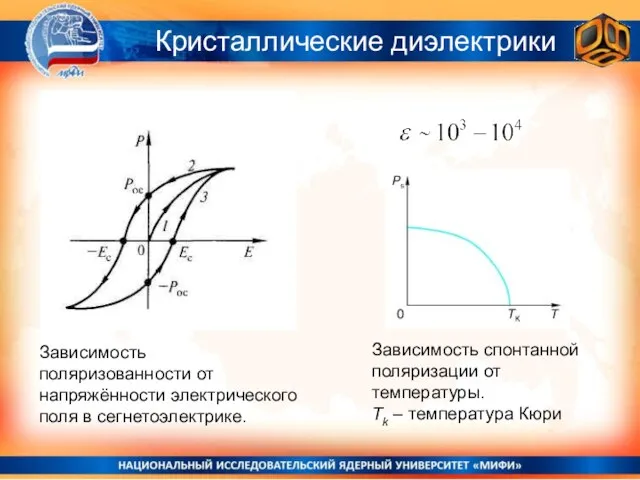
- 28. Кристаллические диэлектрики Зависимость поляризованности от напряжённости электрического поля в сегнетоэлектрике. Зависимость спонтанной поляризации от температуры. Tk
- 29. Спасибо за внимание! Курс общей физики НИЯУ МИФИ Следующая лекция 06 октября
- 30. Проводники и диэлектрики Диэлектрик – вещество, где нет свободных электрических зарядов, способных перемещаться под действием приложенного
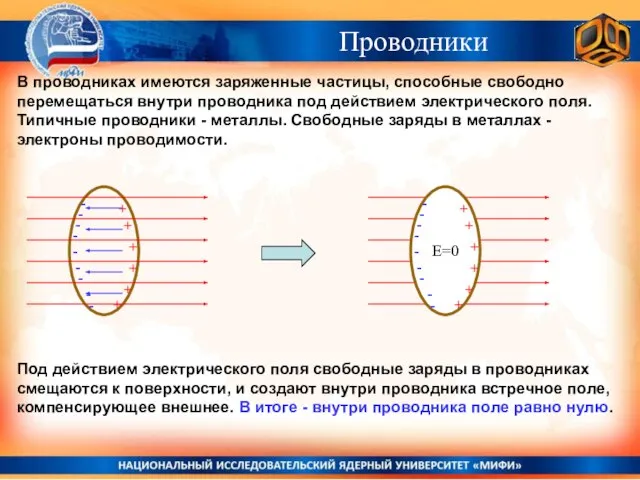
- 31. В проводниках имеются заряженные частицы, способные свободно перемещаться внутри проводника под действием электрического поля. Типичные проводники
- 33. Скачать презентацию




















 Регулярные вариации низкочастотных акустических полей
Регулярные вариации низкочастотных акустических полей Электрическая цепь и ее составные
Электрическая цепь и ее составные Колебательный контур
Колебательный контур Квантовая природа света
Квантовая природа света Радиационное излучение
Радиационное излучение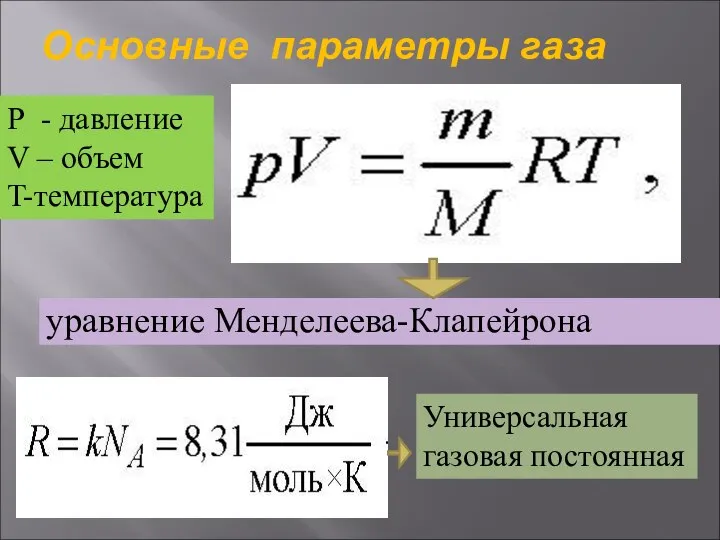 Основные параметры газа
Основные параметры газа Способы соединения частей: шестеренки
Способы соединения частей: шестеренки Явление тяготения. Сила тяжести
Явление тяготения. Сила тяжести Лазеры. Виды лазеров
Лазеры. Виды лазеров Альбом электрических схем для сдачи экзаменов по программе Машинист электропоезда
Альбом электрических схем для сдачи экзаменов по программе Машинист электропоезда Системы высот. Геодезия
Системы высот. Геодезия Классификация тепловых двигателей
Классификация тепловых двигателей Проведение прочностных расчетов машин и механизмов на предприятии
Проведение прочностных расчетов машин и механизмов на предприятии Попов – основатель радиовещания
Попов – основатель радиовещания Обобщающий урок Знатоки физики
Обобщающий урок Знатоки физики Техническое обслуживание смазочной системы МТЗ-80
Техническое обслуживание смазочной системы МТЗ-80 Простые механизмы. КПД
Простые механизмы. КПД Урок4 РПД
Урок4 РПД Презентация на тему Инерция и инертность
Презентация на тему Инерция и инертность  Наблюдение сплошного и линейчатых спектров. Лабораторная работа
Наблюдение сплошного и линейчатых спектров. Лабораторная работа Полупроводники
Полупроводники OVZ_Zanyatie_3
OVZ_Zanyatie_3 Энергия колебательного движения
Энергия колебательного движения Современные требования к проектной документации по размещению передающих радиотехнических объектов
Современные требования к проектной документации по размещению передающих радиотехнических объектов Презентация на тему Колебательный контур. Электромагнитные колебания
Презентация на тему Колебательный контур. Электромагнитные колебания  Презентация на тему Теплопередача и ее виды
Презентация на тему Теплопередача и ее виды  Основное уравнение динамики вращательного движения твердого тела. (Лекция 7)
Основное уравнение динамики вращательного движения твердого тела. (Лекция 7) Физика плазмы
Физика плазмы