Содержание
- 2. Интерференция света (от лат. inter – взаимно, между собой и ferio – ударяю, поражаю) – пространственное
- 3. Интерференция двух волн на поверхности жидкости, возбуждаемых вибрирующими стержнями Волны распространяются в противоположных направлениях и интерферируют
- 4. Интерференция поверхностных волн от двух точечных источников В точках, для которых r2 - r1 = λ
- 5. Интерференция круговой волны в жидкости с её отражением от стенки Расстояние от источника до стенки r
- 6. Интерференция круговой волны в жидкости с её отражением от стенки Расстояние между точечным источником и стенкой
- 7. 8.1 Интерференция световых волн Волновые свойства света наиболее отчетливо обнаруживают себя в интерференции и дифракции. Пусть
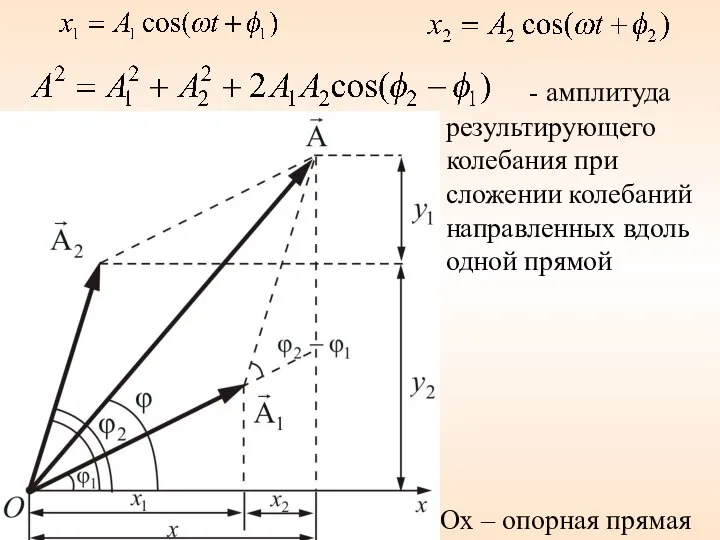
- 8. Ox – опорная прямая - амплитуда результирующего колебания при сложении колебаний направленных вдоль одной прямой
- 9. Если разность фаз колебаний возбужденных волнами в некоторой точке пространства остается постоянной во времени, то такие
- 10. В случае когерентных волн (7.2.2) Последнее слагаемое в этом выражении -интерференционный член. ; в минимуме ,
- 11. Для некогерентных источников интенсивность результирующей волны всюду одинакова и, равна сумме интенсивностей, создаваемых каждой из волн
- 12. И так суть интерференции света : Знаем: Интерференцией света называется… Условие мах Δ12 = m λ
- 13. В обычном «естественном» свете вектор Е направлен равновероятно во все стороны. - «Ёжик» векторов (фото за
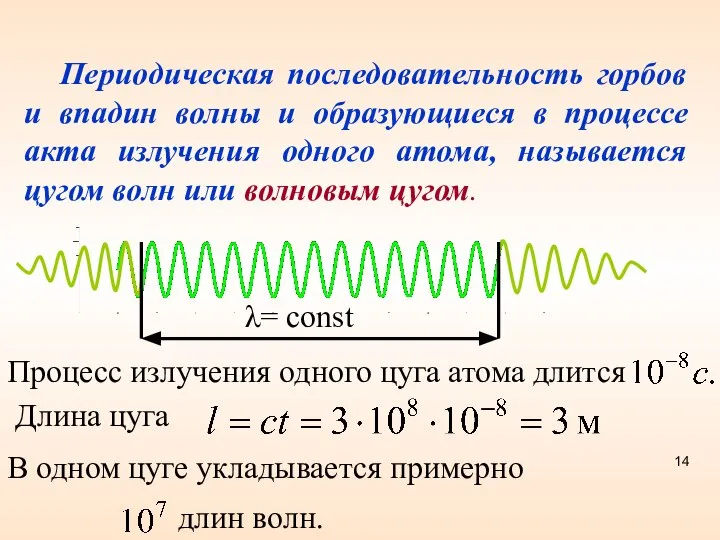
- 14. Периодическая последовательность горбов и впадин волны и образующиеся в процессе акта излучения одного атома, называется цугом
- 15. Одной из важных характеристик наблюдаемой интерференционной картины является видность V, которая характеризует контраст интерференционных полос: где
- 16. Рисунок 7.3 Первая волна Разность фаз двух когерентных волн - Оптическая разность хода - L –
- 17. Условие максимума и минимума интерференции: Если оптическая разность хода равна целому числу длин волн (7.2.3) -
- 18. 8.2 Опыт Юнга
- 19. 620-780 нм 585-620 нм 575-585 нм 550-575 нм 510-550 нм 480-510 нм 450-480 нм 380-450 нм
- 20. Опыт Юнга
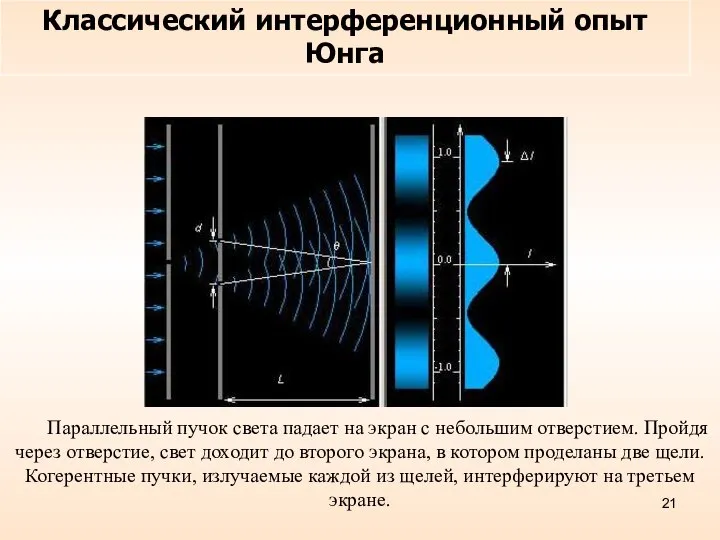
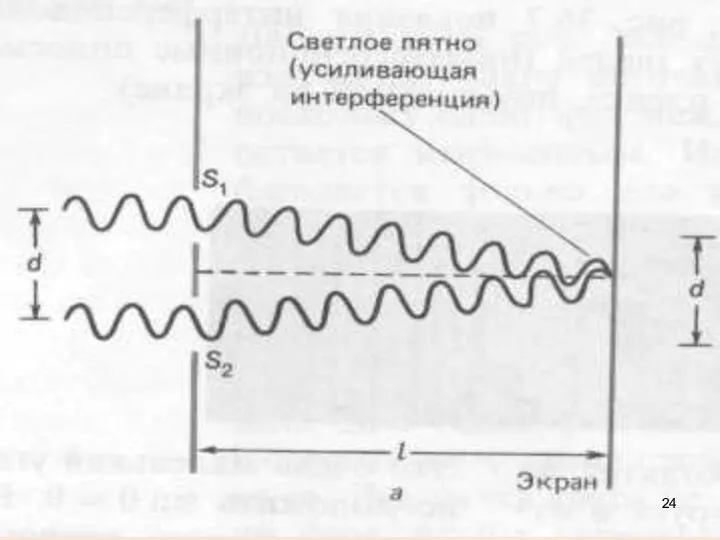
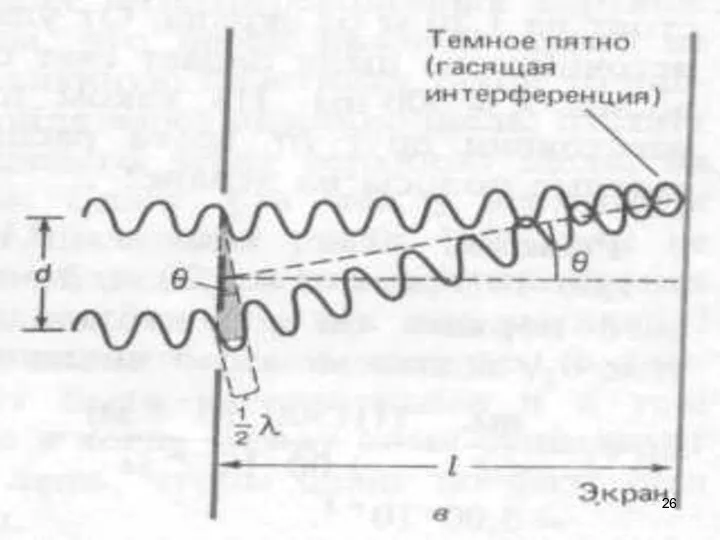
- 21. Параллельный пучок света падает на экран с небольшим отверстием. Пройдя через отверстие, свет доходит до второго
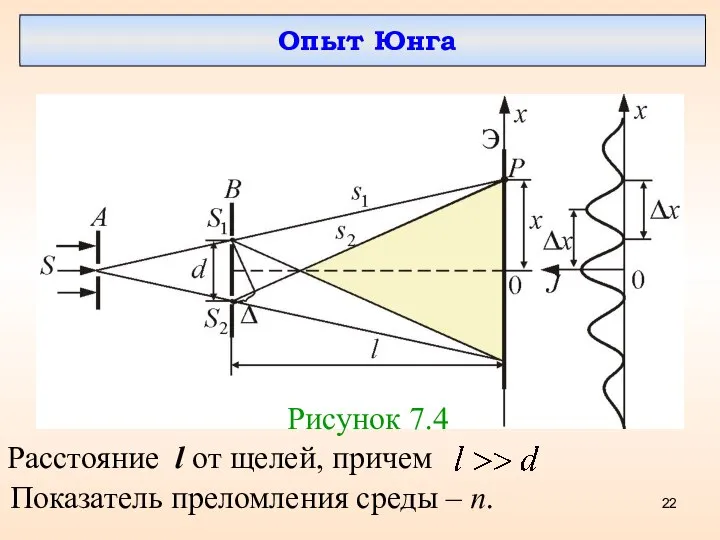
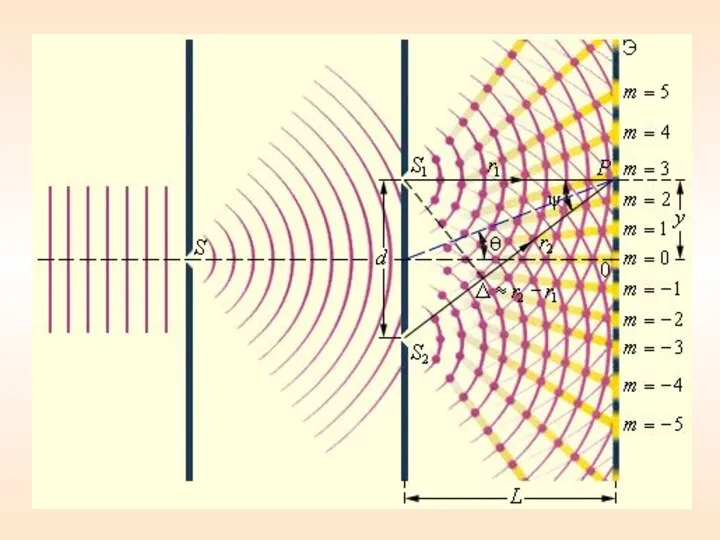
- 22. Опыт Юнга Рисунок 7.4 Расстояние l от щелей, причем Показатель преломления среды – n.
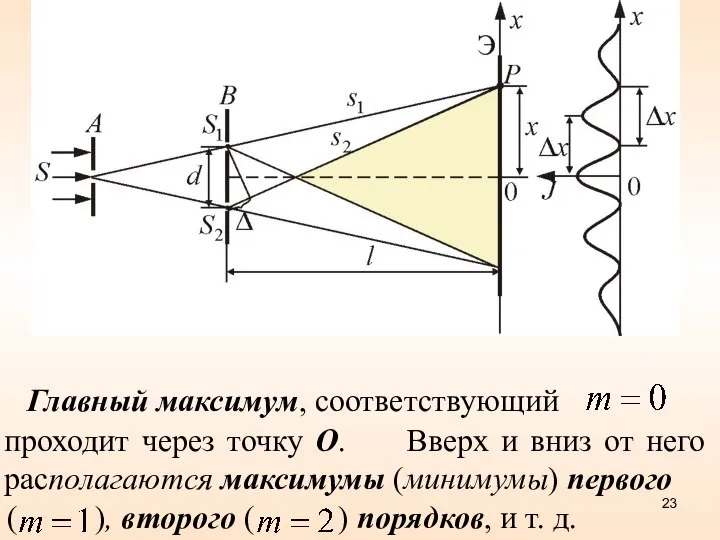
- 23. Главный максимум, соответствующий проходит через точку О. Вверх и вниз от него располагаются максимумы (минимумы) первого
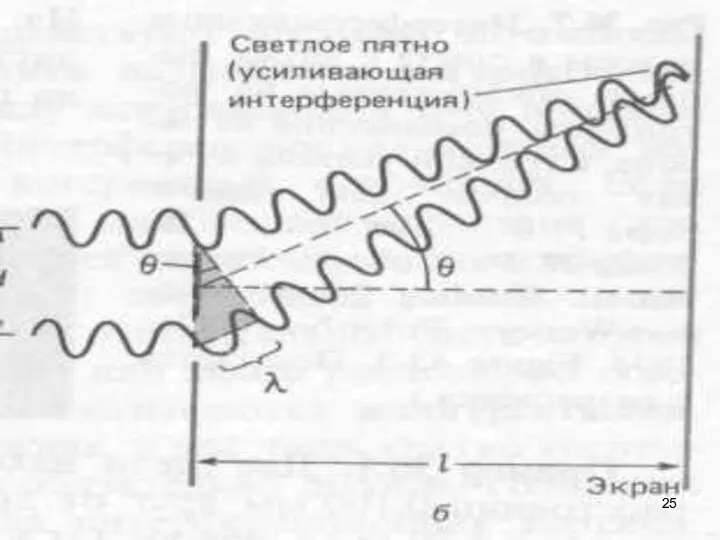
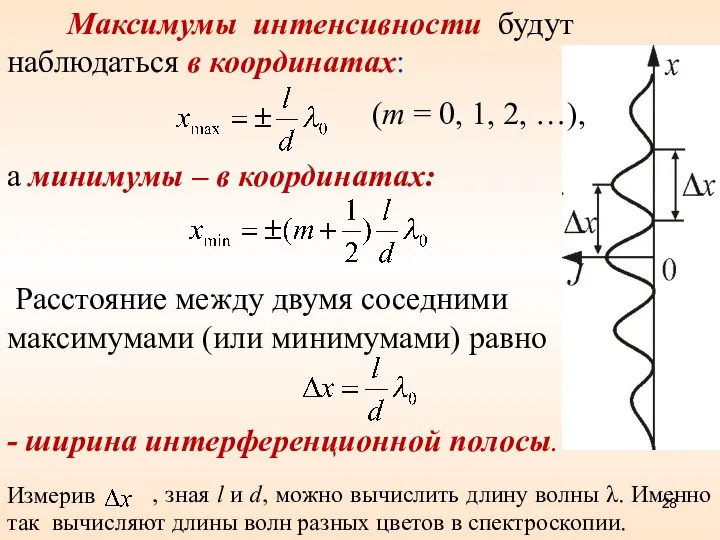
- 28. Расстояние между двумя соседними максимумами (или минимумами) равно Максимумы интенсивности будут наблюдаться в координатах: (m =
- 29. 8.3 Когерентность и монохроматичность Необходимым условием интерференции волн является их когерентность, т.е. согласованное протекание во времени
- 30. Волну можно приближенно считать монохроматической только в течение времени (7.4.1) где – время когерентности За промежуток
- 31. (7.4.2) где – длина когерентности (длина гармонического цуга, образующегося в процессе излучения одного атома) – расстояние
- 32. Можно показать ,что чем шире интервал частот, представленных в данной волне, тем меньше время когерентности. Предельный
- 33. Два источника, размеры и взаимное расположение которых позволяют наблюдать интерференцию, называются пространственно-когерентными. Радиусом когерентности (или длиной
- 34. Критерий наблюдения интерференции при протяженном источнике: b - допустимый размер источника; λ – длина волны; Ω
- 35. Условия пространственной когерентности двух волн 1) постоянная во времени разность фаз: ω1t +φ01 – ω2 t
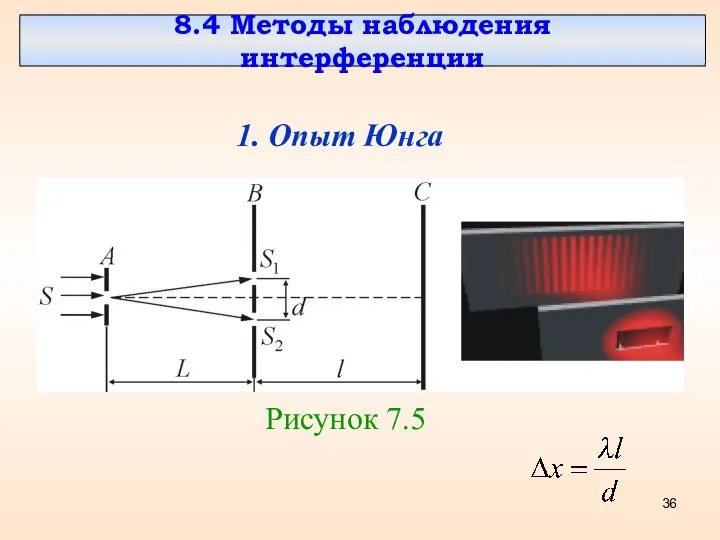
- 36. 8.4 Методы наблюдения интерференции 1. Опыт Юнга Рисунок 7.5
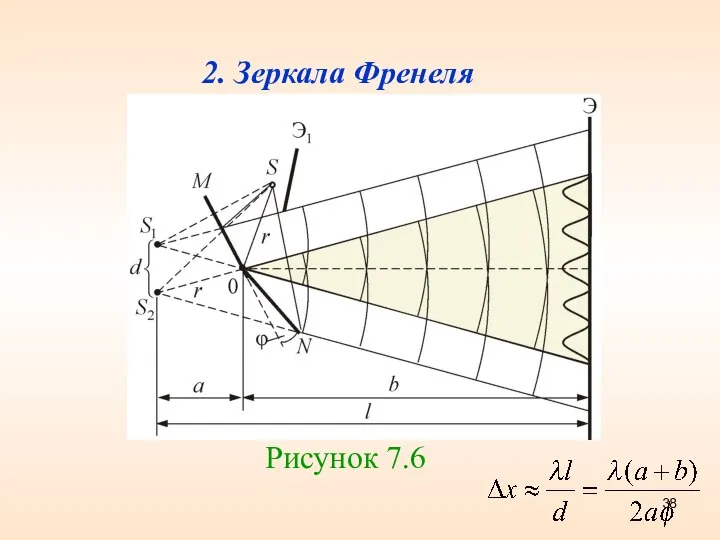
- 38. 2. Зеркала Френеля Рисунок 7.6
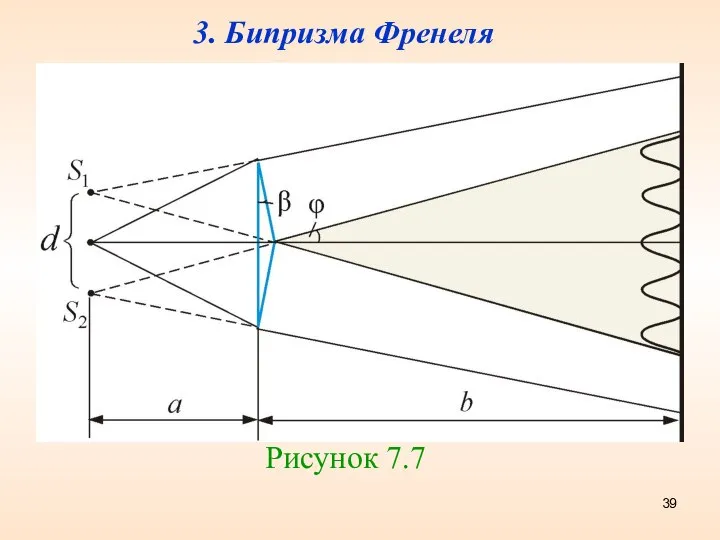
- 39. 3. Бипризма Френеля Рисунок 7.7
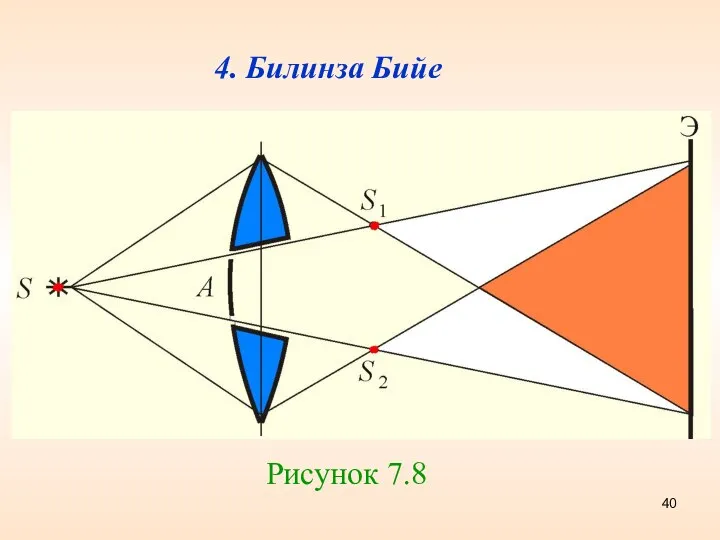
- 40. 4. Билинза Бийе Рисунок 7.8
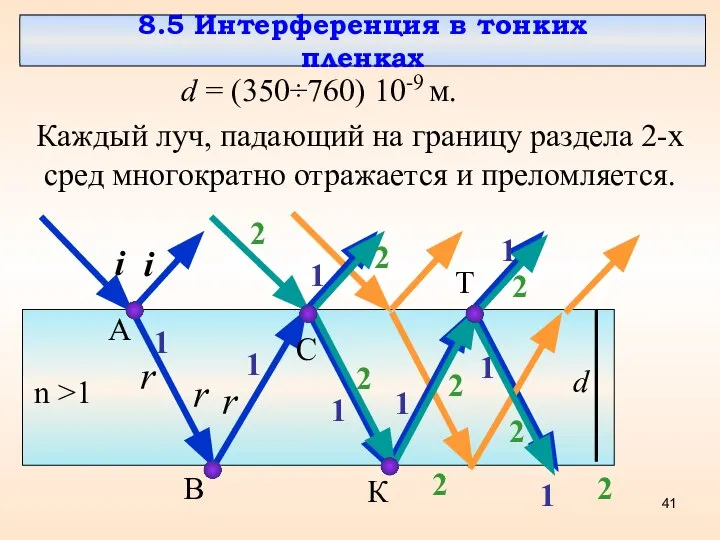
- 41. 8.5 Интерференция в тонких пленках d = (350÷760) 10-9 м. Каждый луч, падающий на границу раздела
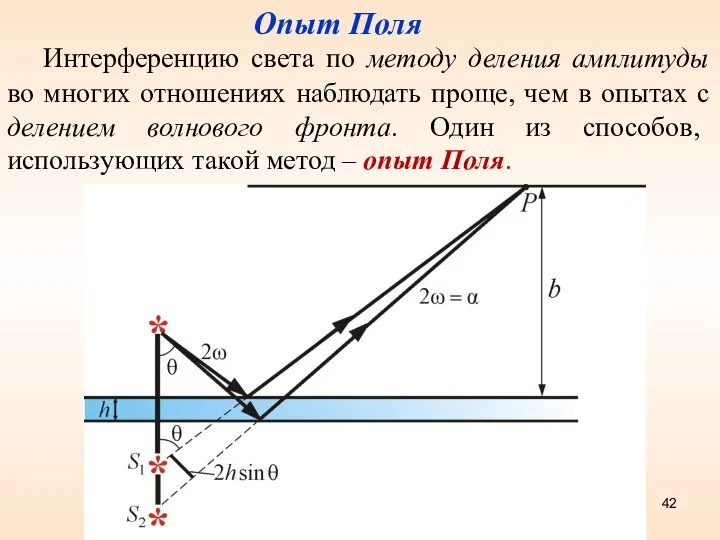
- 42. Опыт Поля Интерференцию света по методу деления амплитуды во многих отношениях наблюдать проще, чем в опытах
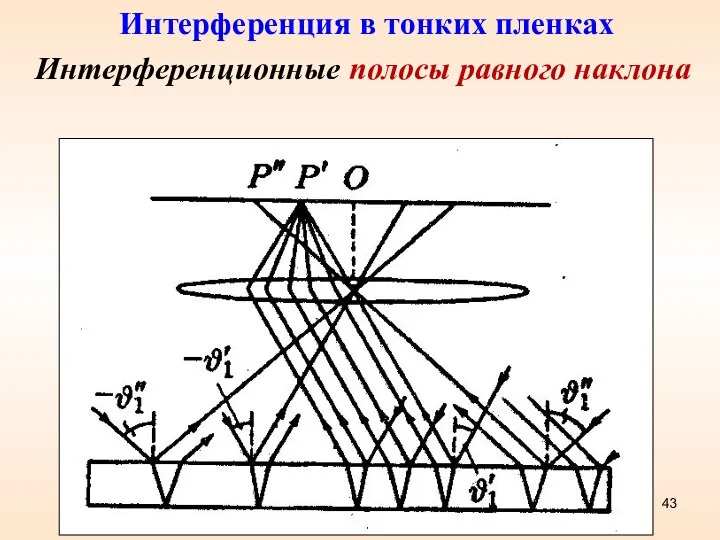
- 43. Интерференционные полосы равного наклона Интерференция в тонких пленках
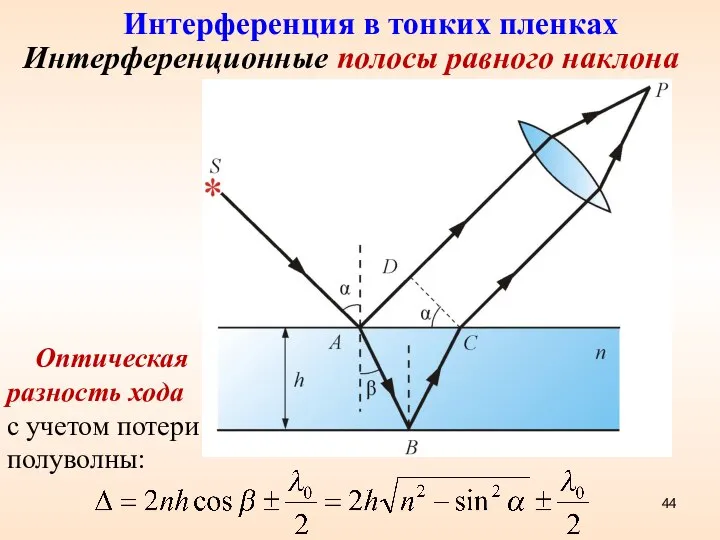
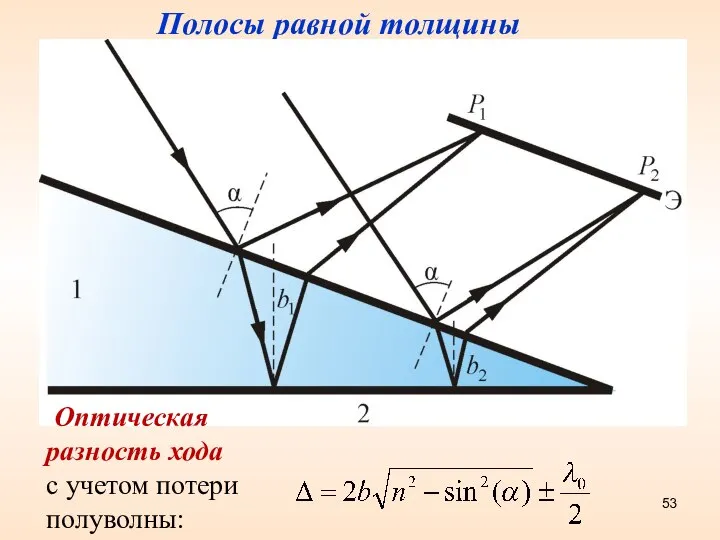
- 44. Интерференционные полосы равного наклона Интерференция в тонких пленках Оптическая разность хода с учетом потери полуволны:
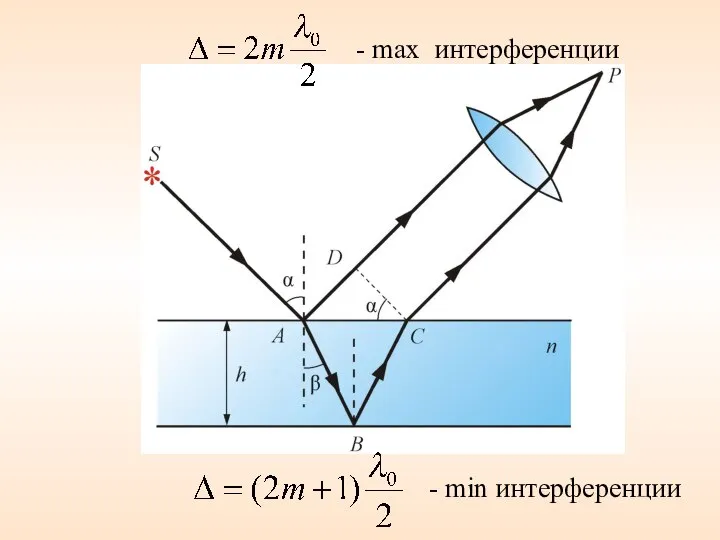
- 45. - max интерференции - min интерференции
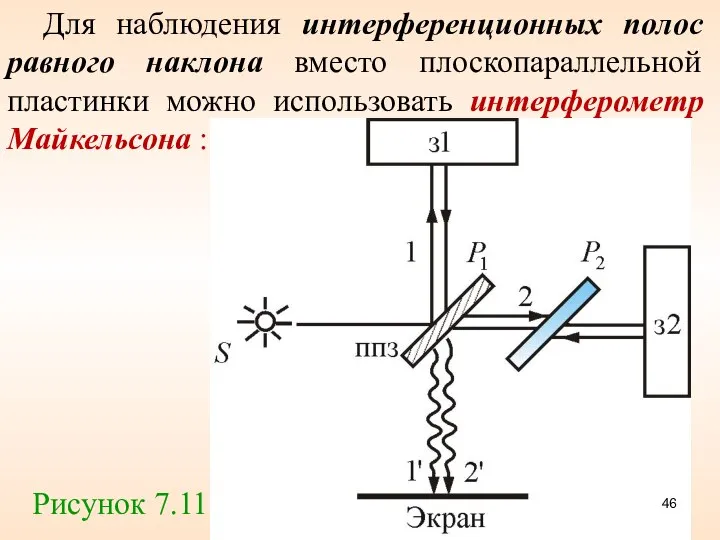
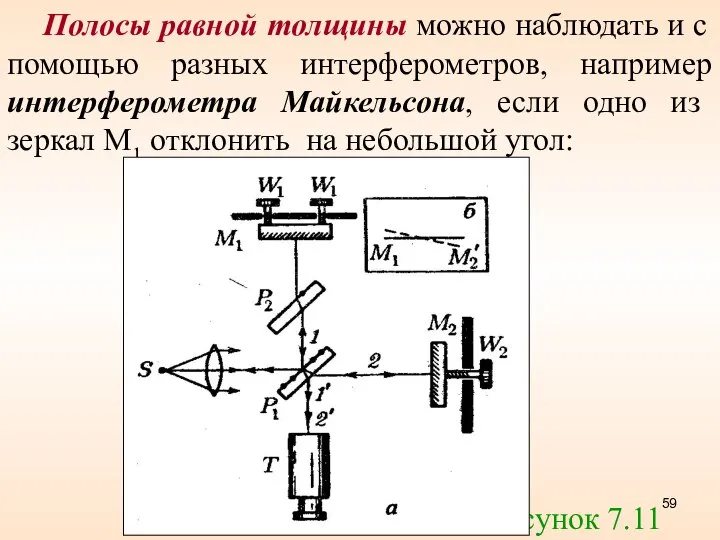
- 46. Для наблюдения интерференционных полос равного наклона вместо плоскопараллельной пластинки можно использовать интерферометр Майкельсона : Рисунок 7.11
- 47. Цвета тонких пленок В белом свете интерференционные полосы, при отражении от тонких пленок - окрашены. Поэтому
- 48. Опыты с мыльной пленкой
- 49. Изменение картины интерференции по мере уменьшения толщины мыльной пленки
- 50. нефть на воде
- 51. 34 Интерференция от клина.
- 52. Интерференция на клине Максимумы в отраженном свете dmin = 4n
- 53. Полосы равной толщины Оптическая разность хода с учетом потери полуволны:
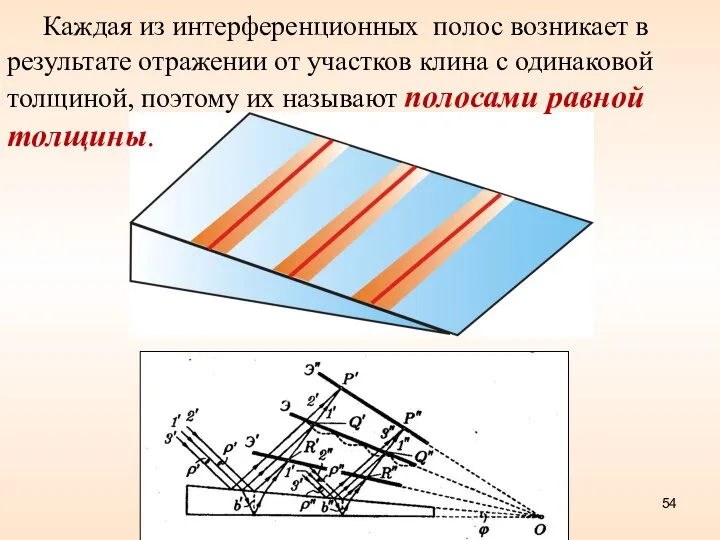
- 54. Каждая из интерференционных полос возникает в результате отражении от участков клина с одинаковой толщиной, поэтому их
- 55. Рис. а - световые лучи, отражаясь от верхней и нижней поверхностей тонкого воздушного клина, интерферируют и
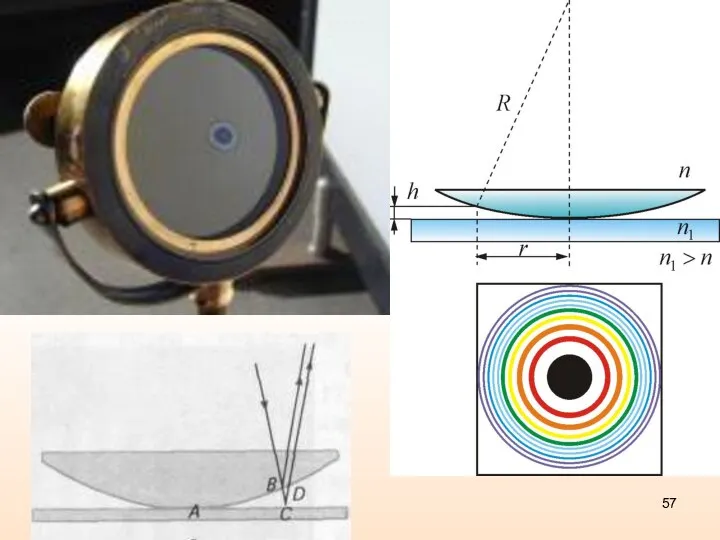
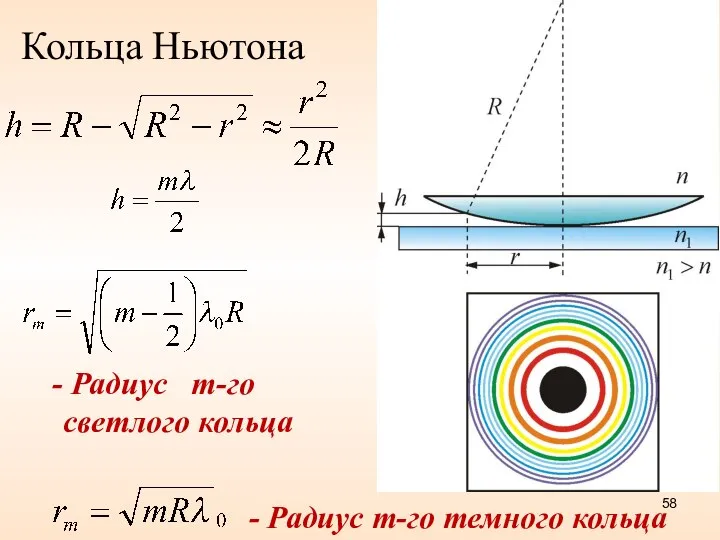
- 56. Кольца Ньютона Ньютон объяснил это явление на основе корпускулярной теории света. Кольцевые полосы равной толщины, наблюдаемые
- 58. Кольца Ньютона - Радиус m-го темного кольца Радиус m-го светлого кольца
- 59. Полосы равной толщины можно наблюдать и с помощью разных интерферометров, например интерферометра Майкельсона, если одно из
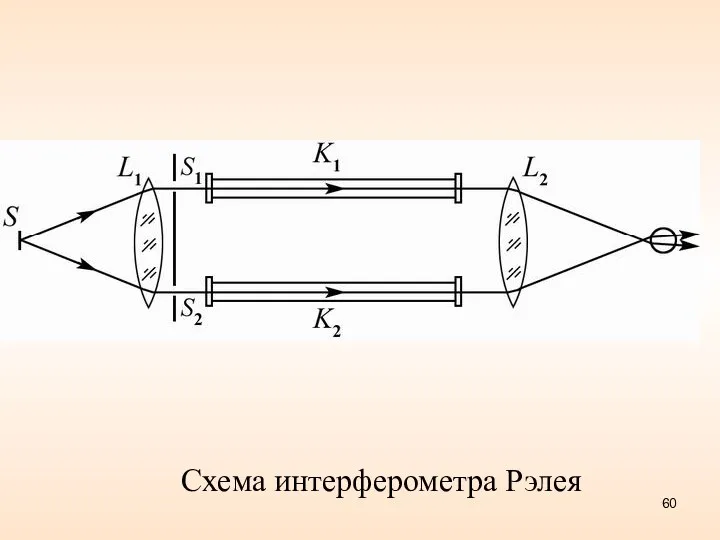
- 60. Схема интерферометра Рэлея
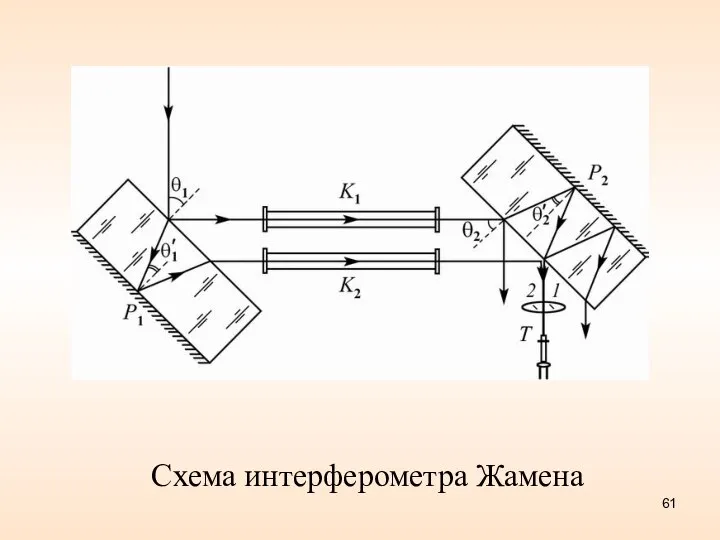
- 61. Схема интерферометра Жамена
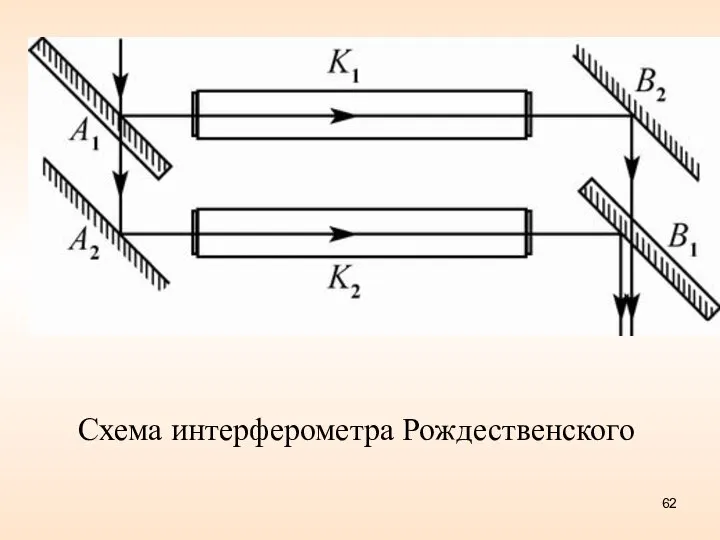
- 62. Схема интерферометра Рождественского
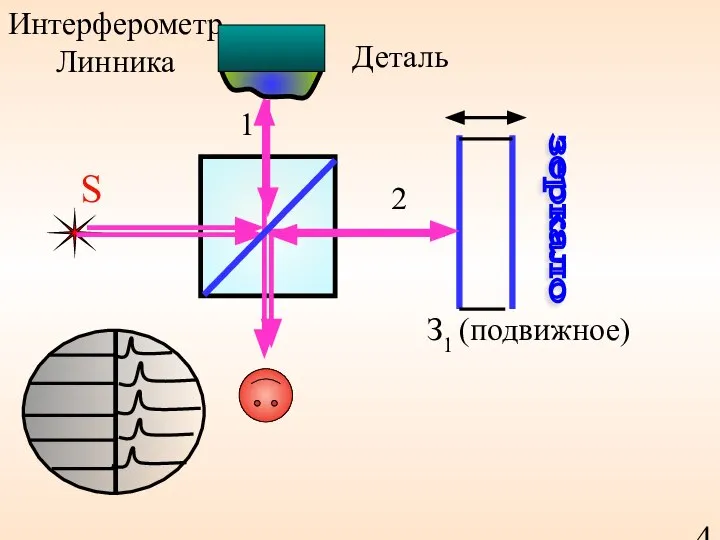
- 63. Интерферометр Линника S зеркало З1 (подвижное) Деталь 1 2 40
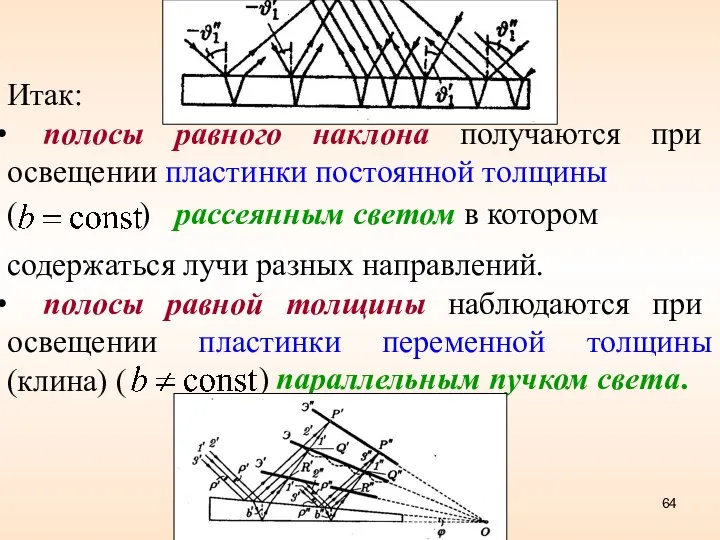
- 64. Итак: полосы равного наклона получаются при освещении пластинки постоянной толщины ( ) рассеянным светом в котором
- 65. 8.6 Применение интерференции света 1. Тот факт, что расположение интерференционных полос зависит от длины волны и
- 66. 2. По интерференционной картине можно выявлять и измерять неоднородности среды (в т.ч. фазовые), в которой распространяются
- 70. 3. Явление интерференции волн, рассеянных от некоторого объекта (или прошедших через него), с «опорной» волной лежит
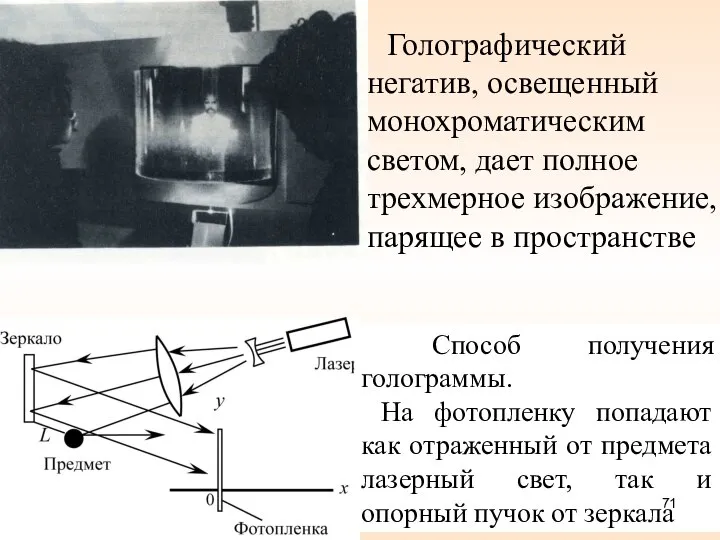
- 71. Голографический негатив, освещенный монохроматическим светом, дает полное трехмерное изображение, парящее в пространстве Способ получения голограммы. На
- 72. 4. Интерференционные волны от отдельных «элементарных» излучателей используется при создании сложных излучающих систем (антенн) для электромагнитных
- 73. В 1963 г. начал работать 300-метровый радиотелескоп со сферической антенной в Аресибо на острове Пуэрто-Рико, установленный
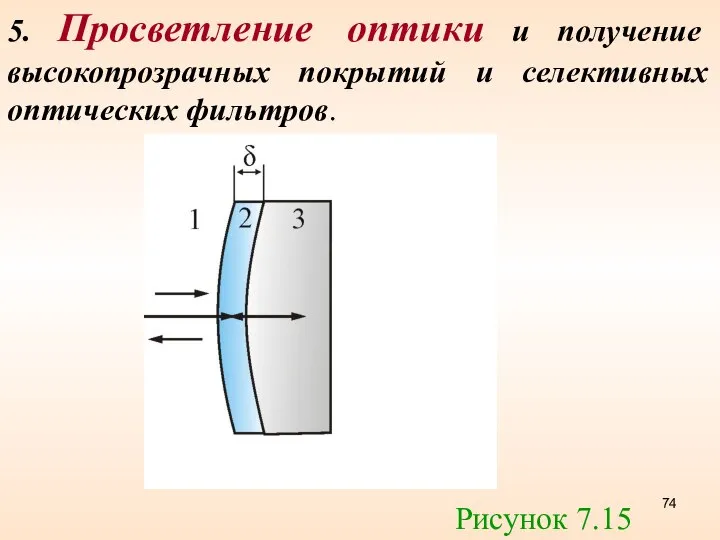
- 74. 5. Просветление оптики и получение высокопрозрачных покрытий и селективных оптических фильтров. Рисунок 7.15
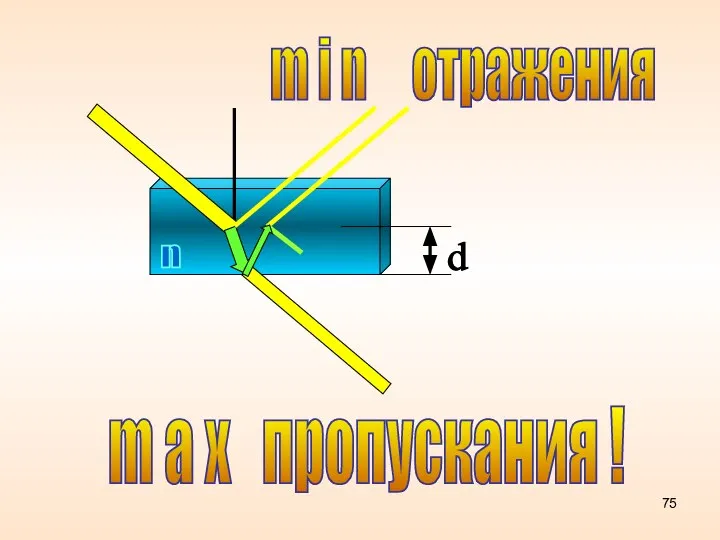
- 75. m i n отражения m a x пропускания !
- 76. m a x пропускания света в рабочий объем Просветление линз и солнечных батарей Min интерференции
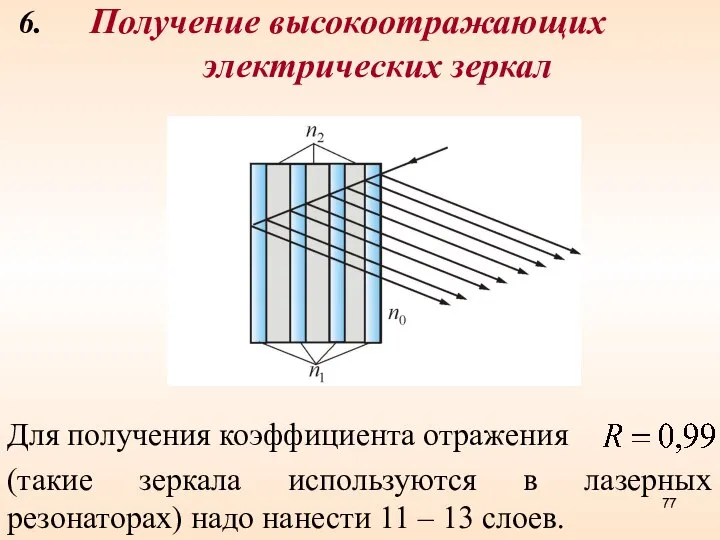
- 77. 6. Получение высокоотражающих электрических зеркал Для получения коэффициента отражения (такие зеркала используются в лазерных резонаторах) надо
- 78. Знать: 2. Какими параметрами описывается световая волна? 1. Законы геометрической оптики. 3. Что такое цуг волн
- 79. 7. Как записываются условия max и min в тонких пленках в отраженном и проходящем свете для
- 80. Уметь: 1. Строить ход лучей в пластинках, линзах, зеркалах, призмах. 2. Построить ход интерферирующих лучей в
- 81. 5. Изображать на рис. схему установки для получения колец Ньютона. 6 Построить ход лучей в интерферометрах
- 82. Радиус иона меди: (+2e) 72 (+1e) 96 пм Радиус иона: (+2e) 69 пм 620-780 нм 585-620
- 83. Выводы: Изучена скорость охлаждения насыщенного раствора сернокислого никеля и медного купороса, Определены оптимальные условия выращивания кристаллов
- 84. Спасибо за внимание.
- 86. Скачать презентацию
















































 Вакуумная базука
Вакуумная базука Звуковые колебания. Источники звука (9 класс)
Звуковые колебания. Источники звука (9 класс) Средства измерений физических величин
Средства измерений физических величин Излучение и поглощение электромагнитных волн в среде. (Лекция 2)
Излучение и поглощение электромагнитных волн в среде. (Лекция 2) Презентация на тему Свойства зрения
Презентация на тему Свойства зрения  Линзы. Оптическая сила линзы. 9 класс
Линзы. Оптическая сила линзы. 9 класс Решение задач по теме Фотоэффект
Решение задач по теме Фотоэффект Визначення сталой в законі Стефана-Больцмана. Лабораторна робота № 50
Визначення сталой в законі Стефана-Больцмана. Лабораторна робота № 50 Презентация к уроку _Инерциальные системы отсчета
Презентация к уроку _Инерциальные системы отсчета Элементы теории электромагнетизма Максвелла. Лекция 14
Элементы теории электромагнетизма Максвелла. Лекция 14 15 минут про структуру атома
15 минут про структуру атома Статистическая теория радиотехнических систем. Нормальный случайный процесс. (Лекция 7)
Статистическая теория радиотехнических систем. Нормальный случайный процесс. (Лекция 7) Обслуживание тормозной системы
Обслуживание тормозной системы Система пуска двигателя
Система пуска двигателя Загадки
Загадки Интеллектуальные технологии смешанной реальности для аэрокосмических систем
Интеллектуальные технологии смешанной реальности для аэрокосмических систем Тепловые процессы
Тепловые процессы Тонкослойная хроматография
Тонкослойная хроматография Электрический ток
Электрический ток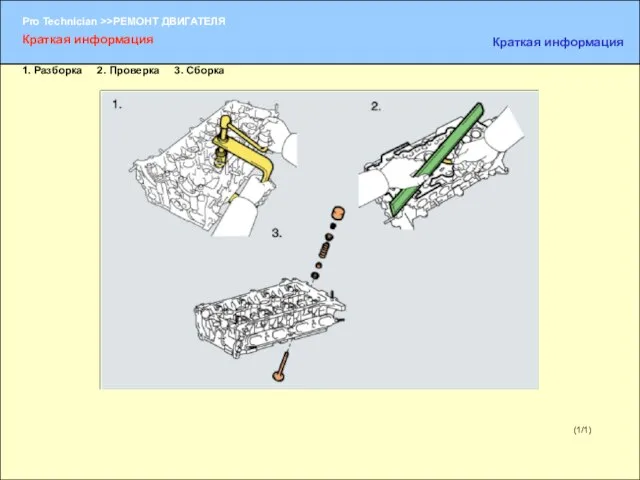 Краткая информация Ремонт двигателя
Краткая информация Ремонт двигателя Интерференция света в тонких пленках. Лаборатория природы
Интерференция света в тонких пленках. Лаборатория природы Тема урока: Электрическое сопротивление Открываем новое свойство тел!
Тема урока: Электрическое сопротивление Открываем новое свойство тел! Магнитная проницаемость
Магнитная проницаемость Законы Ньютона
Законы Ньютона Графит и алмаз. Кристаллы
Графит и алмаз. Кристаллы Закон сохранения энергии
Закон сохранения энергии Электромобиль
Электромобиль Презентация на тему Сложение сил, направленных вдоль одной прямой. Равнодействующая сила
Презентация на тему Сложение сил, направленных вдоль одной прямой. Равнодействующая сила