Содержание
- 2. Диференціальне рівняння вимушених коливань
- 3. Розв’язок диференціального рівняння вимушених коливань Оскільки рівняння неоднорідне, його розв’язок являє собою лінійну комбінацію загального розв’язку
- 4. Розв’язок диференціального рівняння вимушених коливань Часова залежність заряду для усталених коливань описується виразом: де залежність амплітуди
- 5. Резонанс Як видно, амплітуда усталених вимушених коливань залежить від частоти зовнішньої періодичної сили (або зовнішньої ЕРС
- 6. Резонансом називається явище стрімкого зростання амплітуди вимушених коливань при зміні частоти коливань та наближенні частоти зовнішньої
- 7. Тепер проаналізуємо зміну амплітуди струму: Поділимо чисельник та знаменник на частоту, після чого знову продиференціюємо підкореневий
- 9. Скачать презентацию






 Эксимерные лазеры
Эксимерные лазеры Основные принципы конструирования низкотемпературных устройств. Теплопритоки
Основные принципы конструирования низкотемпературных устройств. Теплопритоки Плотность вещества
Плотность вещества Наночастицы в космосе
Наночастицы в космосе Схемы расположения отклонений для валов и отверстий
Схемы расположения отклонений для валов и отверстий История создания швейной машины
История создания швейной машины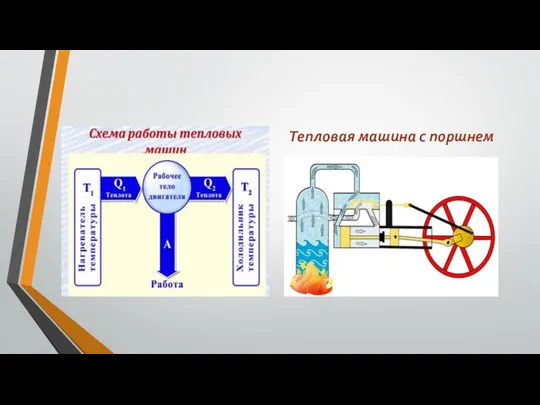 Тепловая машина с поршнем
Тепловая машина с поршнем Електромагнітна індукція
Електромагнітна індукція Телефон без электричества. Физика
Телефон без электричества. Физика Фундаментальные опыты в молекулярной физике
Фундаментальные опыты в молекулярной физике Формулы для расчета рем передачи
Формулы для расчета рем передачи Теоретический чертеж. Координатные оси
Теоретический чертеж. Координатные оси Движение искусственных спутников
Движение искусственных спутников Лазер
Лазер Теоретические основы механики грунтов
Теоретические основы механики грунтов Презентация на тему Сообщающиеся сосуды и их применение
Презентация на тему Сообщающиеся сосуды и их применение  Презентация на тему Элементы специальной теории относительности
Презентация на тему Элементы специальной теории относительности  Рамка с током в однородном магнитном поле
Рамка с током в однородном магнитном поле Урок-конференция Радиация и ее воздействия на биологические объекты Учитель Прокопец Н.Д.
Урок-конференция Радиация и ее воздействия на биологические объекты Учитель Прокопец Н.Д. Консультация по физике
Консультация по физике физические величины измерение физических величин 6 класс презентация (1)
физические величины измерение физических величин 6 класс презентация (1) Излучение и все о нем
Излучение и все о нем Фотоэффект. Опыты А.Г. Столетова (1888-1889)
Фотоэффект. Опыты А.Г. Столетова (1888-1889) Расчет магнитной цепи
Расчет магнитной цепи Микромир. Молекулы, атомы, элементарные частицы. (Тема 2)
Микромир. Молекулы, атомы, элементарные частицы. (Тема 2) Презентация на тему Свободное падение
Презентация на тему Свободное падение  Аналоговая обработка сигналов
Аналоговая обработка сигналов Работа сил тяжести и упругости. Потенциальная энергия
Работа сил тяжести и упругости. Потенциальная энергия