Содержание
- 2. 1- Lois de Kirchhoff Le physicien allemand Gustav Kirchhoff a établi en 1845 deux lois qui
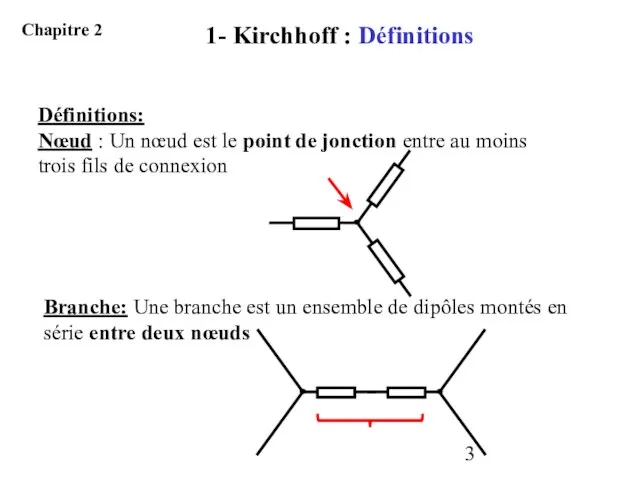
- 3. Définitions: Nœud : Un nœud est le point de jonction entre au moins trois fils de
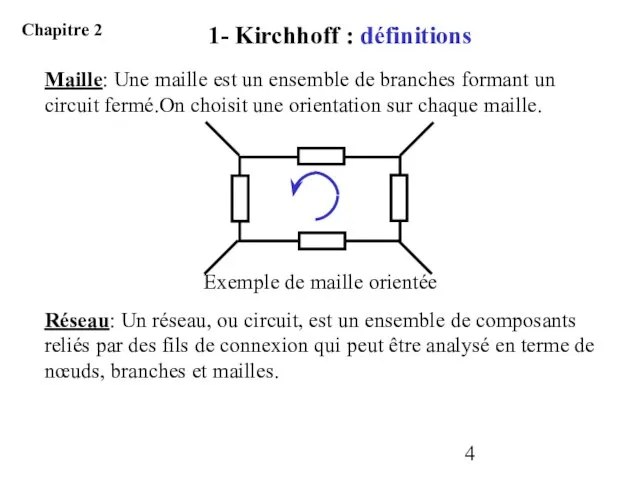
- 4. Maille: Une maille est un ensemble de branches formant un circuit fermé.On choisit une orientation sur
- 5. Lois de Kirchhoff: 1°) La Loi des nœuds: C ’est une conséquence de la conservation de
- 6. Plus généralement la loi des nœuds s’écrit: Σεkik = 0 εk vaut +1 si le courant
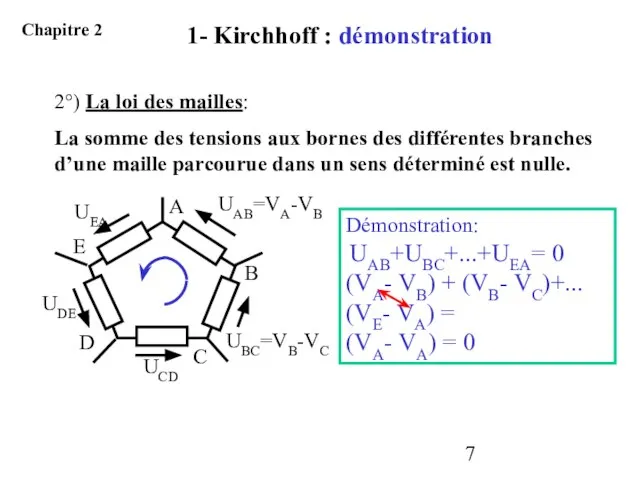
- 7. 2°) La loi des mailles: La somme des tensions aux bornes des différentes branches d’une maille
- 8. Plus généralement la loi des mailles s’écrit: Σεkuk = 0 εk vaut +1 si la tension
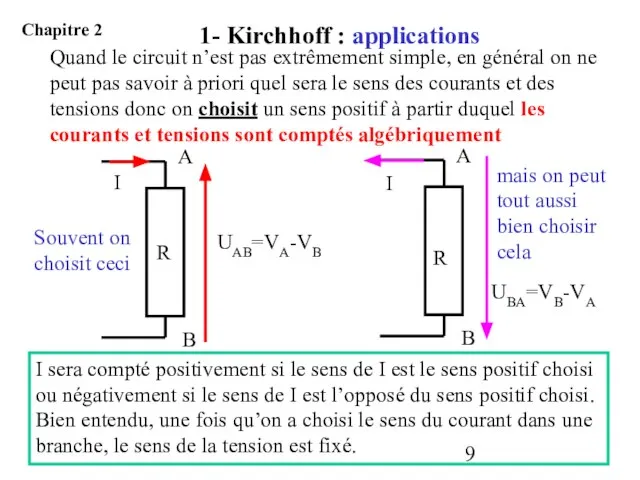
- 9. I sera compté positivement si le sens de I est le sens positif choisi ou négativement
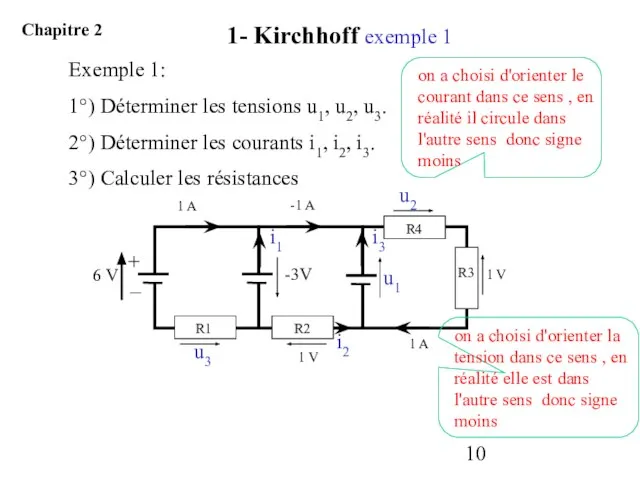
- 10. Exemple 1: 1°) Déterminer les tensions u1, u2, u3. 2°) Déterminer les courants i1, i2, i3.
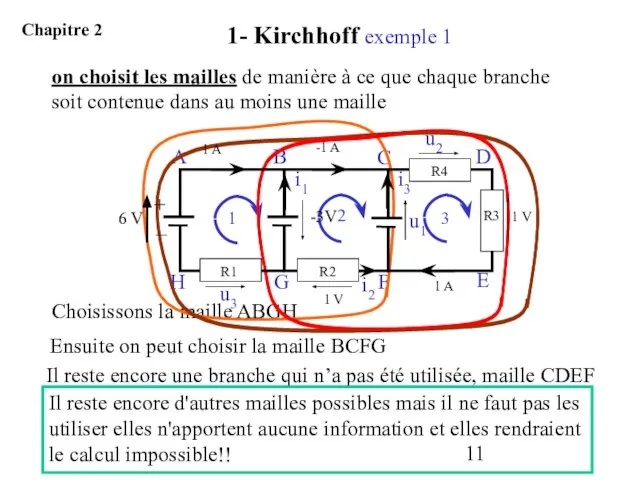
- 11. on choisit les mailles de manière à ce que chaque branche soit contenue dans au moins
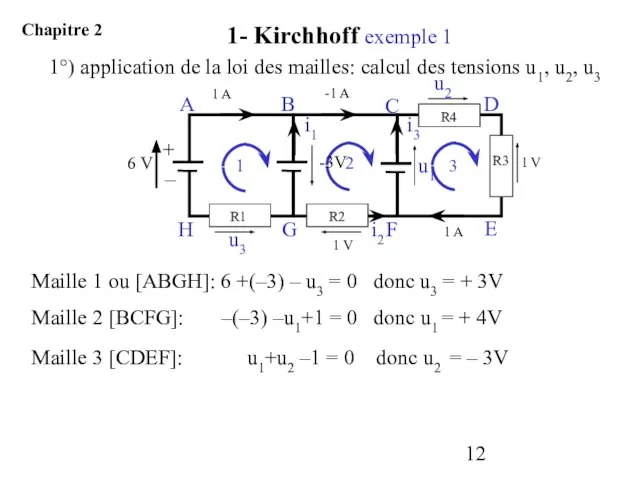
- 12. 1°) application de la loi des mailles: calcul des tensions u1, u2, u3
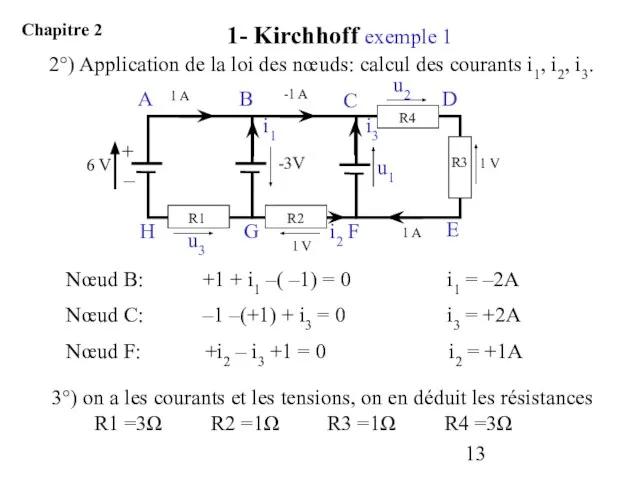
- 13. 2°) Application de la loi des nœuds: calcul des courants i1, i2, i3. Nœud B: +1
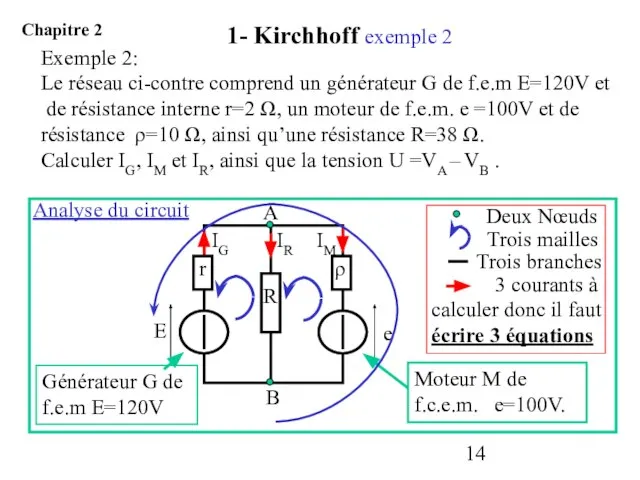
- 14. Exemple 2: Le réseau ci-contre comprend un générateur G de f.e.m E=120V et de résistance interne
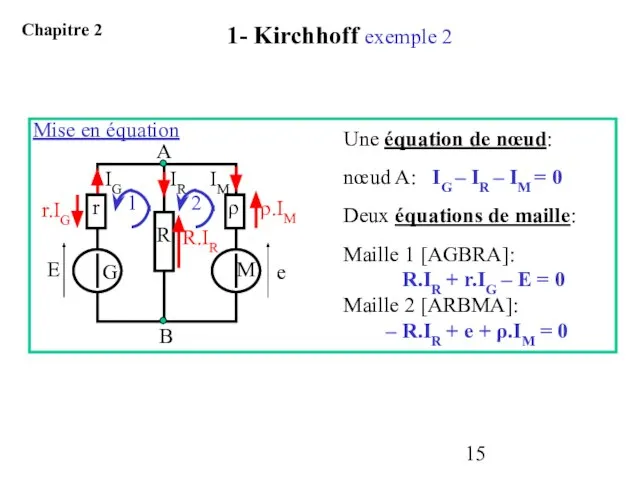
- 15. Mise en équation Une équation de nœud: nœud A: IG – IR – IM = 0
- 16. Résolution du système d ’équations
- 17. 2- Théorème de Thévenin Publié en 1883 par l'ingénieur français Léon Charles Thévenin Tout circuit linéaire
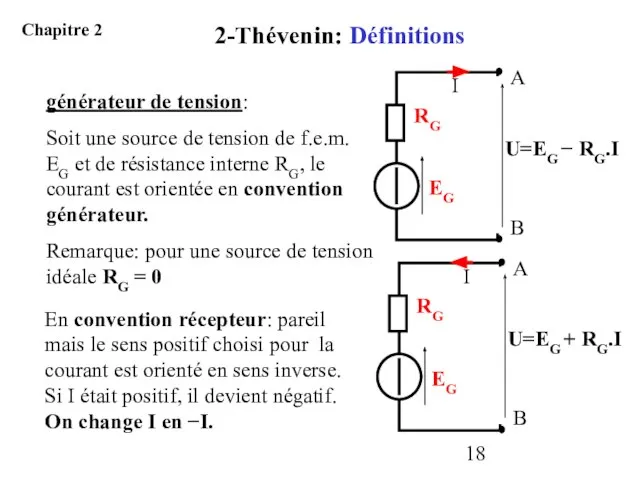
- 18. générateur de tension: Soit une source de tension de f.e.m. EG et de résistance interne RG,
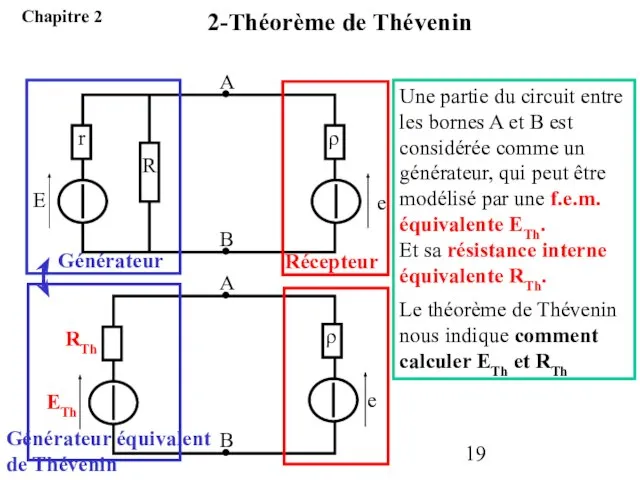
- 19. Une partie du circuit entre les bornes A et B est considérée comme un générateur, qui
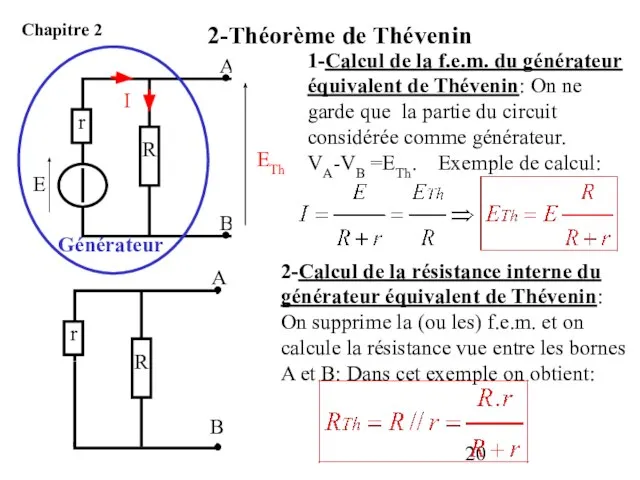
- 20. 1-Calcul de la f.e.m. du générateur équivalent de Thévenin: On ne garde que la partie du
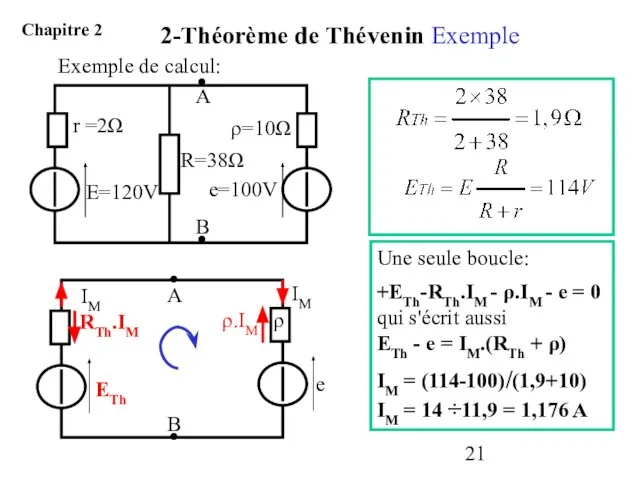
- 21. Exemple de calcul: Une seule boucle: +ETh-RTh.IM - ρ.IM - e = 0 qui s'écrit aussi
- 22. 3- Théorème de superposition Dans un réseau linéaire alimenté par plusieurs sources indépendantes, le courant circulant
- 23. Soit un circuit linéaire comportant plusieurs sources autonomes de tension et de courant. Le courant dans
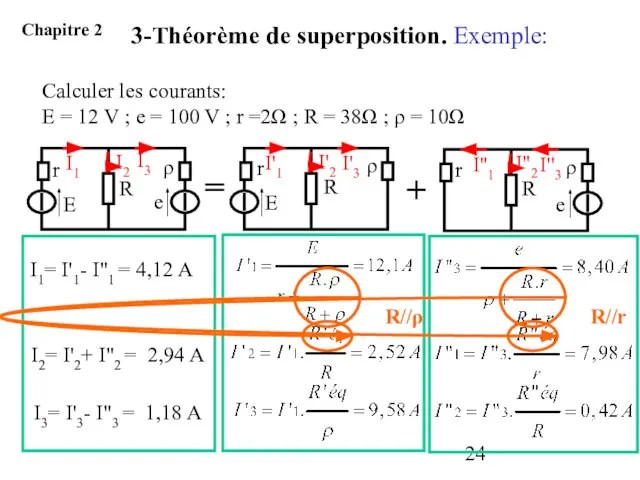
- 24. Calculer les courants: E = 12 V ; e = 100 V ; r =2Ω ;
- 25. 4- Théorème de Norton Le théorème a été publié en 1926 par l'ingénieur des laboratoires Bell,
- 26. *2
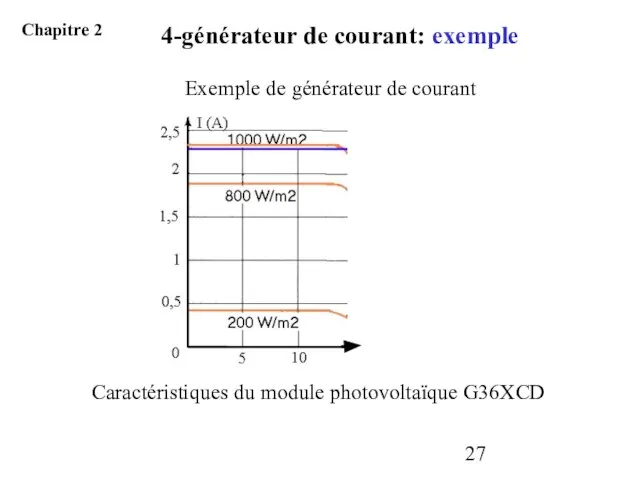
- 27. Caractéristiques du module photovoltaïque G36XCD Exemple de générateur de courant
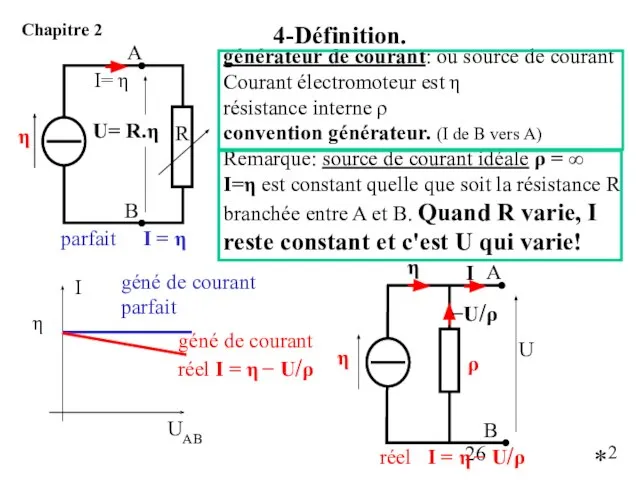
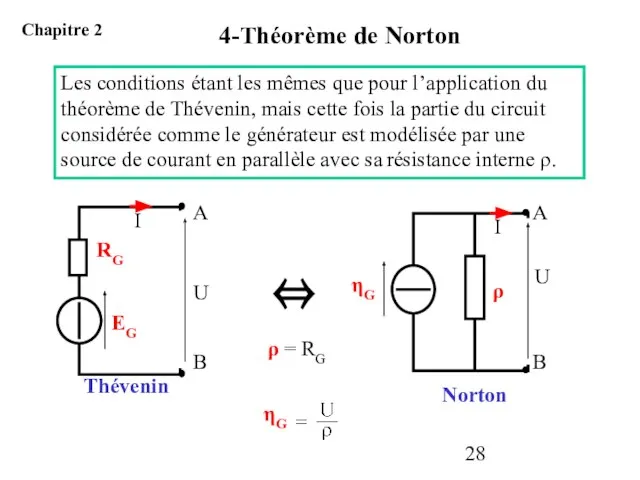
- 28. Les conditions étant les mêmes que pour l’application du théorème de Thévenin, mais cette fois la
- 29. 5- Théorème de Millman
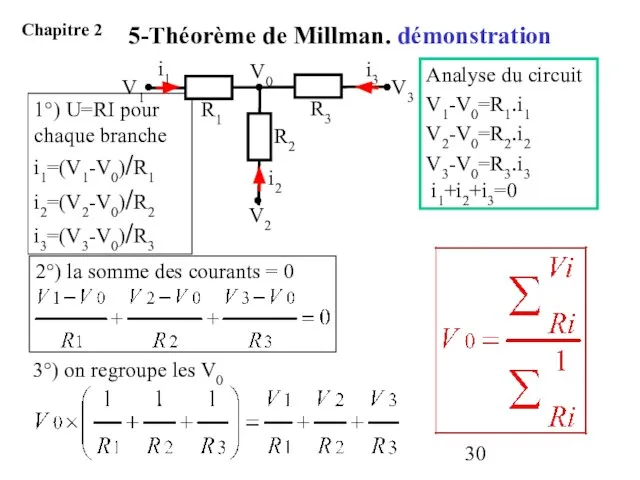
- 30. Analyse du circuit V1-V0=R1.i1 V2-V0=R2.i2 V3-V0=R3.i3 i1+i2+i3=0 1°) U=RI pour chaque branche i1=(V1-V0)/R1 i2=(V2-V0)/R2 i3=(V3-V0)/R3
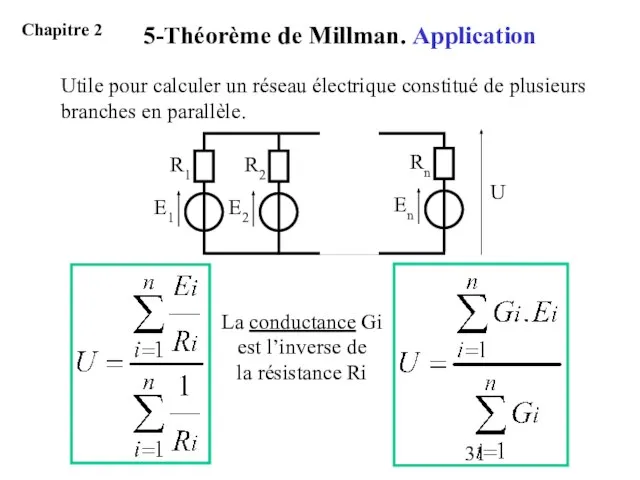
- 31. Utile pour calculer un réseau électrique constitué de plusieurs branches en parallèle. La conductance Gi est
- 33. Скачать презентацию










 Лекция 9. Выпаривание
Лекция 9. Выпаривание Строительная механика, ее цели, задачи и методы
Строительная механика, ее цели, задачи и методы Электростатическое поле в диэлектрике. Лекция 3-2020
Электростатическое поле в диэлектрике. Лекция 3-2020 Презентация на тему газовые законы
Презентация на тему газовые законы  Свободное падение 10-9
Свободное падение 10-9 Морской бой. Игра по физике
Морской бой. Игра по физике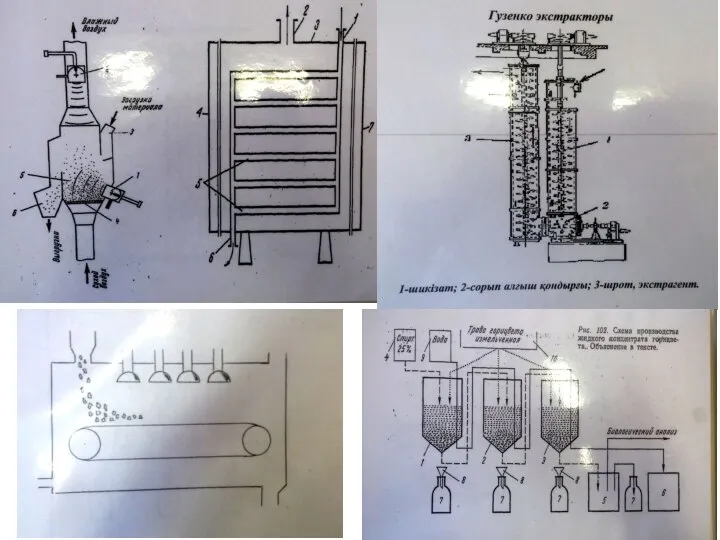 Эстракторы. Схемы
Эстракторы. Схемы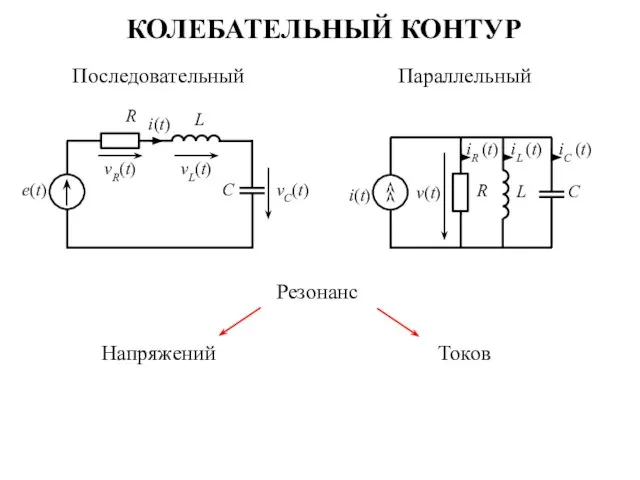 Колебательный контур
Колебательный контур Экскаваторы
Экскаваторы Уравнения переменного тока. Задачи
Уравнения переменного тока. Задачи Прямолинейное равноускоренное движение. Ускорение
Прямолинейное равноускоренное движение. Ускорение День космонавтики. Двигатели I ступени
День космонавтики. Двигатели I ступени Характеристики электромагнитных реле постоянного тока. Лекция 7 (2)
Характеристики электромагнитных реле постоянного тока. Лекция 7 (2) Идеальный газ. Абсолютная температура. Макро и микропараметры
Идеальный газ. Абсолютная температура. Макро и микропараметры ЭДС индукции в движущихся проводниках
ЭДС индукции в движущихся проводниках Класична рівноважна термодинаміка. Повторення основ фізичної хімії
Класична рівноважна термодинаміка. Повторення основ фізичної хімії Закон збереження енергії
Закон збереження енергії Характеристики телескопов. Задания
Характеристики телескопов. Задания Фазовые и структурные превращения в оболочках ТВЭЛов из сплава Э110 в условиях сухого хранения
Фазовые и структурные превращения в оболочках ТВЭЛов из сплава Э110 в условиях сухого хранения Электротехника и электрооборудование автомобилей
Электротехника и электрооборудование автомобилей Отгадай имя физика. Игра
Отгадай имя физика. Игра МКТ строения вещества
МКТ строения вещества Спектры. Устройство спектроскопа
Спектры. Устройство спектроскопа Физика – это наука о природе!
Физика – это наука о природе! Автоматическое управление движением судном
Автоматическое управление движением судном zakony_nyutona_9_k
zakony_nyutona_9_k Разработка и исследование системы управления технологического процесса с помощью термодинамических характеристик
Разработка и исследование системы управления технологического процесса с помощью термодинамических характеристик Законы Кирхгофа
Законы Кирхгофа