Содержание
- 2. если источники электрической энергии синусоидальны, но хотя бы один из элементов цепи нелинеен, т.е., если цепь
- 3. ИЗОБРАЖЕНИЕ НЕСИНУСОИДАЛЬНЫХ ТОКОВ И НАПРЯЖЕНИЙ С ПОМОЩЬЮ РЯДОВ ФУРЬЕ Любую периодическую функцию f(t) с периодом T,
- 4. Угловую частоту ω = 2πf называют основной угловой частотой, а синусоидальные и косинусоидальные составляющие с основной
- 5. а амплитуды синусоидальных и косинусоидальных членов ряда соответственно: (1.3) (1.4) Положим t0 = 0 и введем
- 6. (1.6) (1.7) (1.8) Гармонический ряд Фурье (1.1) может быть записан и в иной форме. Поскольку где
- 7. то: (1.9) Форма ряда (1.9) более предпочтительна для расчета электрических цепей с несинусоидальными источниками токов, так
- 8. ПРАКТИЧЕСКИЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ГАРМОНИК РЯДА ФУРЬЕ Встречающиеся в электротехнике источники электрической энергии, генерирующие периодические несинусоидальные токи
- 9. Приближенный метод определения гармоник ряда Фурье основан на замене определенных интегралов, вычисляемых согласно (1.6 – 1.8),
- 10. где k — текущий индекс, принимающий значения от 1 до m; fk(α) – значение функции f(α)
- 11. При расчетах по (1.10) – (1.12) обычно бывает достаточно разделить период функции на m = 24
- 12. СЛУЧАИ СИММЕТРИИ Периодические несинусоидальные функции, изображающие электрические и магнитные величины, обладают обычно каким-либо видом симметрии, что
- 13. Такие функции называются четными. Поскольку синусоиды любых частот являются нечетными функциями, при таком виде симметрии в
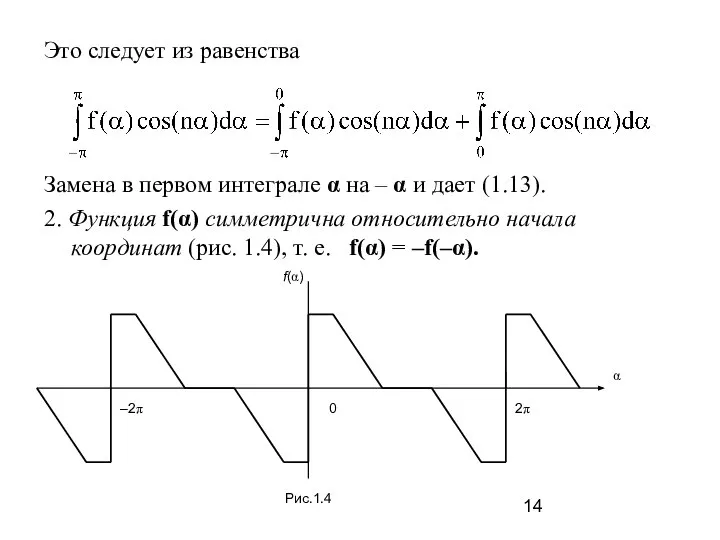
- 14. Это следует из равенства Замена в первом интеграле α на – α и дает (1.13). 2.
- 15. Такие функции называются нечетными. Поскольку постоянная составляющая и косинусоиды этому условию не удовлетворяют, то при данном
- 16. 3. Функция f(α) симметрична относительно оси абсцисс при совмещении двух полупериодов во времени (рис. 1.5), т.
- 17. Это условие удовлетворяется при произвольных значениях a только в том случае, если А0 = 0 и
- 18. ПРИМЕНЕНИЕ РЯДА ФУРЬЕ К РАСЧЕТУ ПЕРИОДИЧЕСКОГО НЕСИНУСОИДАЛЬНОГО ПРОЦЕССА Пусть требуется найти ток в электрической цепи под
- 19. Применительно к одноконтурной цепи Под Z(0) подразумевается сопротивление цепи при частоте, равной нулю, т.е. сопротивление постоянному
- 20. При этом Z(0) = ∞, так как цепь для постоянного тока разомкнута. Рассмотрим отдельно идеальную катушку
- 21. В отличие от катушки индуктивности, сопротивление конденсатора убывает с ростом порядкового номера гармоники. . Соответственно имеем:
- 22. Если, например, в цепи для гармоники порядка n = q имеет место резонанс напряжений, то сопротивление
- 23. разложение ЭДС или токов источников (если заданы токи) на гармонические составляющие; расчет в комплексной форме токов
- 24. Поскольку составляющие несинусоидального тока (напряжения) имеют неодинаковые частоты, суммировать следует их мгновенные значения, а не комплексные
- 25. ДЕЙСТВУЮЩЕЕ И СРЕДНЕЕ ЗНАЧЕНИЯ ПЕРИОДИЧЕСКОЙ НЕСИНУСОИДАЛЬНОЙ ФУНКЦИИ Действующее (среднеквадратичное) значение периодической несинусоидальной функции определяется аналогично действующему
- 26. то Интеграл от последней суммы равен нулю, поскольку а, как известно, С учетом того, что
- 27. окончательно для действующего значения периодической несинусоидальной функции получаем: (1.25) Поскольку Аn — амплитуда гармоники n, то
- 28. Действующее значение периодической несинусоидальной функции может быть измерено, так же как и при гармонических токах, с
- 29. Этот интеграл равен среднему значению функции f(t) за положительный полупериод, если f(t) имеет одинаковые положительную и
- 30. МОЩНОСТЬ В ЦЕПИ ПЕРИОДИЧЕСКОГО НЕСИНУСОИДАЛЬНОГО ТОКА По определению активная мощность равна среднему значению мощности за период:
- 31. Итак, (1.26) т.е. активная мощность периодического несинусоидального тока равна сумме активных мощностей отдельных гармоник плюс мощность
- 32. По аналогии с понятием реактивной мощности для гармонических функций может быть введено понятие реактивной мощности в
- 33. Поэтому, если полную мощность в рассматриваемой цепи определить как произведение действующих значений напряжения и тока S
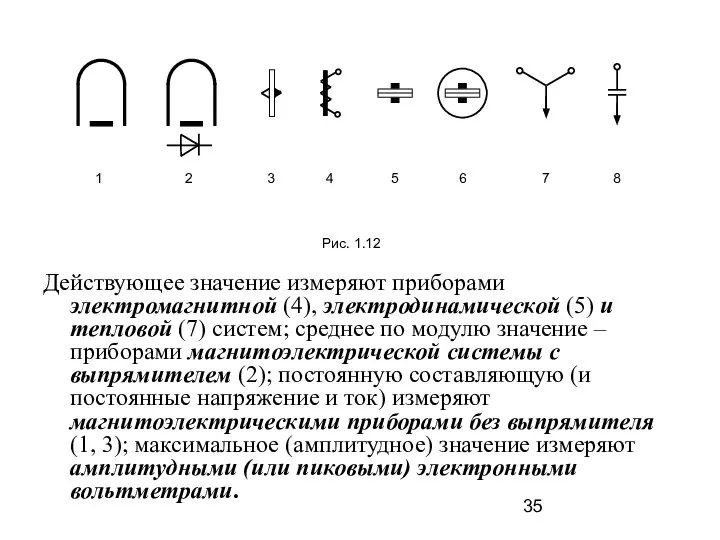
- 34. ИЗМЕРЕНИЕ ТОКОВ И НАПРЯЖЕНИЙ В ЦЕПЯХ НЕСИНУСОИДАЛЬНОГО ТОКА Для измерения несинусоидальных токов и напряжений применяются электроизмерительные
- 35. Действующее значение измеряют приборами электромагнитной (4), электродинамической (5) и тепловой (7) систем; среднее по модулю значение
- 36. КОЭФФИЦИЕНТЫ, ХАРАКТЕРИЗУЮЩИЕ ПЕРИОДИЧЕСКИЕ НЕСИНУСОИДАЛЬНЫЕ ФУНКЦИИ По аналогии с гармоническими функциями отношение активной мощности при несинусоидальных токах
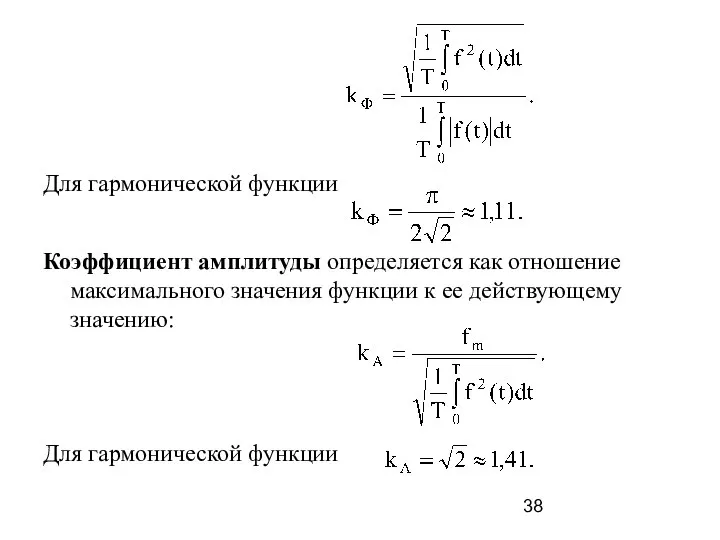
- 37. При этом действующее значение тока Следовательно, коэффициент мощности Множитель называется коэффициентом искажения. Коэффициент формы кривой определяется
- 38. Для гармонической функции Коэффициент амплитуды определяется как отношение максимального значения функции к ее действующему значению: Для
- 40. Скачать презентацию


































 Фотографии для иллюстрации закономерностей оптики
Фотографии для иллюстрации закономерностей оптики Нанотехнологии – толчок в будущее человечества
Нанотехнологии – толчок в будущее человечества Проработка конструкции двигателя ЗМЗ 53. Разработка технологического процесса
Проработка конструкции двигателя ЗМЗ 53. Разработка технологического процесса О, физика – наука из наук!
О, физика – наука из наук! Теория автоматического управления. Дифференцирующие звенья
Теория автоматического управления. Дифференцирующие звенья Подшипники
Подшипники Основы МКТ. Идеальный газ
Основы МКТ. Идеальный газ Определение коэффициента поверхностного натяжения жидкости методом капиллярных явлений и методом отрыва капель
Определение коэффициента поверхностного натяжения жидкости методом капиллярных явлений и методом отрыва капель Відновлення працездатності засобами фізичної рекреації
Відновлення працездатності засобами фізичної рекреації Архимедова сила. Решение задач
Архимедова сила. Решение задач Сравнительная характеристика проводниковых материалов. Медь и алюминий
Сравнительная характеристика проводниковых материалов. Медь и алюминий Электрический ток в газах
Электрический ток в газах Оптические приборы
Оптические приборы Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки
Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки Характеристики электрического тока
Характеристики электрического тока Динамика в задачах
Динамика в задачах Зимний тепловой режим помещения. Лекция13
Зимний тепловой режим помещения. Лекция13 Ретро стиль. Восстановление и ремонт ретро автомобилей. Ремонт современных легковых автомобилей
Ретро стиль. Восстановление и ремонт ретро автомобилей. Ремонт современных легковых автомобилей Электрический заряд
Электрический заряд Привод к шнеку-смесителю
Привод к шнеку-смесителю Электрические методы контроля
Электрические методы контроля Презентация по физике "Физика - это наука понимать природу" -
Презентация по физике "Физика - это наука понимать природу" -  Аналогия между механическими и электромагнитными колебаниями
Аналогия между механическими и электромагнитными колебаниями Криволинейное движение. Центростремительное (нормальное) ускорение
Криволинейное движение. Центростремительное (нормальное) ускорение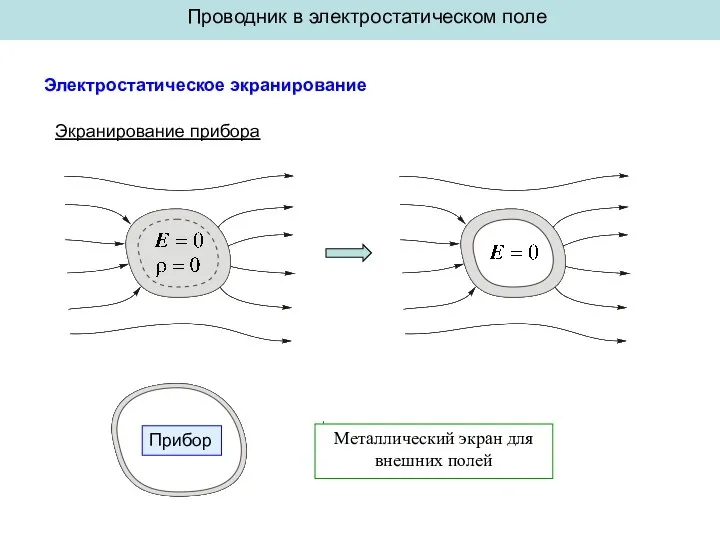 Электростатическое экранирование
Электростатическое экранирование Презентация на тему Паровые машины
Презентация на тему Паровые машины  Презентация на тему Импульс тела
Презентация на тему Импульс тела  Коллоквиум №2
Коллоквиум №2