Gidromekhanika_1

Гидромеханика наука, изучающая равновесие и движение жидкости, а также взаимодействие между жидкостью и твердыми частицами, погруженными в жидкость.

1. Процессы перемещения потоков в трубопроводах и аппаратах;
2. Процессы, протекающие с разделением неоднородных систем (осаждение, классификация, фильтрование, центрифугирование);
Гидромеханические процессы химической технологии можно разделить:

3. процессы, протекающие с образованием неоднородных систем (перемешивание, псевдоожижение и др.).

Законы гидромеханики и их практические приложения изучают в гидравлике.
Гидравлика состоит из гидростатики и гидродинамики.

В гидростатике изучают законы равновесия жидкостей и газов,
в гидродинамике — законы их движения.

Гидростатика

Условия равновесия жидкостей и газов определяются силами, действующими на некоторый объем жидкости.
Силы, действующие на выделенный объем жидкости, в зависимости от области приложения делятся на внешние и внутренние.

Жидкости и газы отличаются сплошностью и текучестью
(легкой подвижностью).

При изучении законов равновесия жидкостей и газов используют понятия об идеальной (гипотетической) и реальной жидкостях.

Идеальная жидкость обладает бесконечно большой текучестью. Она абсолютно несжимаема под действием давления, не изменяет плотности при изменении температуры и не обладает внутренним трением (вязкостью).

Реальные жидкости
делятся на капельные (собственно жидкости) и упругие (газы и пары).
Капельные жидкости практически несжимаемы и обладают малым коэффициентом объемного расширения.
Объем упругих жидкостей сильно изменяется при изменении температуры и давления.

Основные физические свойства жидкостей
Плотность
Удельный вес
Удельный обьем
Вязкость

Плотность
характеризует распределение массы в пространстве, занятом жидкостью или газом
ρ=Δm/ΔV
Единица измерения плотности в СИ
1 кг/м3.

Для капельных жидкостей при технических расчетах р =const.
Например, для воды р= 1000 кг/м3
в широком диапазоне температур
(0—100 °С).
Для упругих жидкостей (газы,пары) плотность зависит от температуры и давления: р=f(P, T)

Плотность упругих жидкостей
ρ =(М/22,4)*(Т0Р/ТР0)
где: М - мольная масса газа (пара), кг/кмоль;
Т0 = 273 К; Р0 = 0,1013 МПа = 760 мм рт. ст.;
Р— среднее давление среды, в таких же
единицах как и Р0
Т - средняя температура, К;
22,4 — мольный объем газа (пара), м3/кмоль.

Плотность смеси газов:
ρсм = y1 ρ1+ y2 ρ2 + y3 ρ3 …
Где: y1, y2, ... — объемные доли компонентов смеси;
ρ1, ρ2... — плотности соответствующих компонентов, в кг/м3.

Удельный вес.
Иногда в технике используют понятие веса G (силы тяжести) единицы объема:
ϒ = ΔG/ΔV = Δmg/ΔV = pg,
где g- ускорение свободного падения
g = 9,81 м/с2.
Единица измерения удельного веса в СИ
1 Н/м3.

Удельный объем.
Для характеристики распределения массы вещества в пространстве иногда применяют удельный объем v, величина которого обратна плотности:
V=1/ρ

Гидростатическое давление.
В результате действия поверхностных и массовых (объемных) сил внутри жидкости возникает гидростатическое давление.
Выделим некоторую площадку ΔF внутри объема покоящейся жидкости.
Независимо от положения площадки в пространстве, в данной точке объема жидкость будет давить на нее с некоторой силой ΔР,

Отношение ΔР / ΔF представляет собой среднее гидростатическое давление, в данной точке. Единица измерения давления в СИ — 1 Па.

Гидростатическое давление в данной точке одинаково по всем направлениям (иначе происходило бы перемещение жидкости).

В разных точках гидростатическое давление различно и является функцией координат:
P=f(х, у, z),
т. е. меняется при
изменении глубины
погружения
в жидкость.

первый член уравнения P/ ρg представляет собой статический (или
пьезометрический) напор, характеризующий удельную потенциальную энергию жидкости (энергию, приходящуюся на единицу веса жидкости).
Основное уравнение гидростатики P/ ρg + z = const

Второй член уравнения z — это геометрический напор. Из уравнения следует, что сумма статического (пьезометрического) и геометрического напоров (в м) для поверхностей любого уровня постоянна.

Уравнение Паскаля
P=P0+ρgh
является выражением общего закона гидростатики и формулируется следующим образом:

Давление в любой точке покоящейся жидкости (и данной горизонтальной плоскости) складывается из внешнего давления Р0 и давления столба жидкости ρgh.

Давление столба жидкости равно весу столба жидкости ρg высотой h (от поверхности до данной точки) и с площадью основания, равной единице.

Закон гидростатики в такой формулировке справедлив как для несжимаемых жидкостей, так и для сжимаемых, т. е. для всех жидкостей, газов и их смесей.

ГИДРОДИНАМИКА

Основные задачи гидродинамики классифицируют как внутреннюю, внешнюю и смешанную.
К внутренней задаче относят движение жидкостей и газов по трубам и каналам
к внешней — движение твердых частиц в газе или жидкости
к смешанной — движение жидкостей и газов через слой.

Вязкость.
Это физическое свойство является мерой сопротивления, оказываемого жидкостью (газом) при относительном
сдвиге отдельных частиц

.
Вязкость является результатом действия силы трения между соприкасающимися слоями жидкости, вследствие чего эти слои движутся с различными скоростями

Для расчета силы трения обычно используют закон Ньютона
Ртр = μF* (Δw/Δn)
Ртр - сила трения,
F- площадь поверхности слоя, м2;
Δw/Δn- градиент скорости;
μ-динамический коэффициент вязкости;
W – скорость слоя жидкости;
Δn – расстояние между двумя слоями жидкости.

В расчетах часто используют кинематический коэффициент
вязкости (кинематическую вязкость):
ν = μ/ρ
Единицы измерения и в СИ ν -1 Па*с
μ 1 м2/с

Динамический коэффициент вязкости для газов при температурах, отличных от 0°С, рассчитывают по формуле:
μt = μ0 (273+C)/(T+C)*(T/273)2/3
Где: μ0 - динамический коэффициент вязкости при 0°С;
Т — температура, К;
С — постоянная Сатерленда, зависящая от свойств газа (например, для воздуха
С = 124, для аммиака 626, для водорода73).

Значения μ для жидкостей и газов при различных температурах, необходимые для расчета, определяют по номограммам
и диаграммам, имеющимся в справочной литературе,
или рассчитывают по приведенным выше формулам.

Влияние температуры и давления.
Зависимость вязкости капельных жидкостей от давления (приблизительно до 10 МПа, т. е. 100 кгс/см2) ничтожна, поэтому в технических расчетах ею пренебрегают.

У капельных жидкостей с повышением температуры уменьшаются силы межмолекулярного сцепления — вязкость понижается
У газов с повышением температуры возрастает число соударений молекул, внутреннее трение увеличивается, вязкость повышается.

Скорость и расход жидкости
Движение жидкости характеризуется скоростями ее частиц.
Уравнение объемного расхода (в м3/с):
V=w*f

Уравнение массового расхода (в кг/с):
M=Vρ=w*f*ρ
Где
ρ - плотность жидкости,
w – скорость (в м/с)
F - площади поперечного сечения (в м2) потока.

Уравнение неразрывности
Возьмем трубопровод переменного сечения Выясним, как происходит изменение скорости при установившемся режиме при переходе от сечения 1 к сечению 2.
М1 = М2 , ρ = сonst
следовательно:
w1f1 = w2f2 = const = V

В установившемся потоке жидкости средние по сечениям
скорости обратно пропорциональны площадям этих сечений.

Уравнение Бернулли:
w2/2g + P/ρg + z= const
Эту величину называют гидродинамическим напором.
Гидродинамический напор включает три слагаемых: z - геометрический напор (или высота); P/ρg— статический напор, характеризует удельную потенциальную энергию давления; w2/2g - скоростной (динамический) напор, или удельная кинетическая энергия.

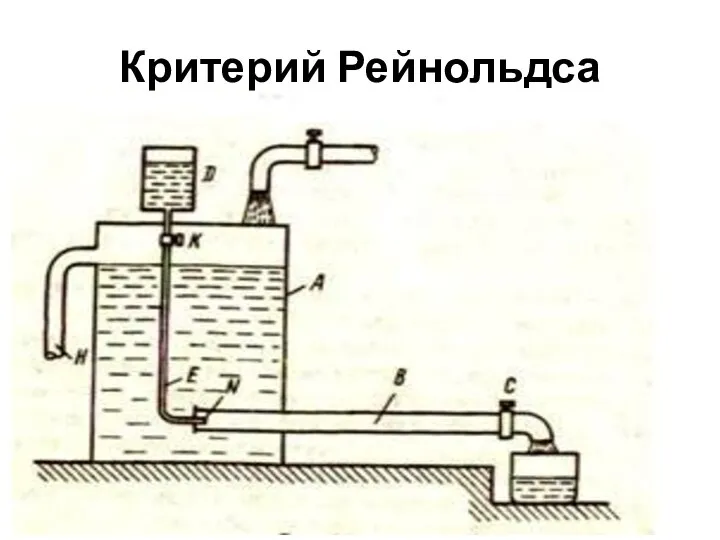
Критерий Рейнольдса

К сосуду 1, в котором поддерживается постоянный уровень воды, присоединена горизонтальная стеклянная труба 2. В эту трубу по ее оси через капиллярную трубку 3 вводится тонкая струйка той же, но окрашенной жидкости. При небольшой скорости жидкости в трубе 2 окрашенная струйка располагается горизонтально и, не размываясь, достигает конца трубы. Все частицы жидкости движутся параллельно и прямолинейно.

Такое движение называется ламинарным (от латинского слова lamina — полоска,
пластинка).

Если скорость
жидкости в трубе увеличивать, то с некоторого предела окрашенная струйка приобретает волнообразное движение, а затем начинает размываться, смешиваясь с основной массой жидкости.

Это движение называется турбулентным (от латинского слова turbulentus —вихревой).
Такое движение характеризуется безразмерной переменной – критерием Рейнольдса:

wdρ/μ = wd/ν = Re
где:
w - средняя скорость потока, м/с;
d - диаметр трубопровода, м;
ρ - плотность потока, кг/м3;
μ - динамический коэффициент вязкости, Па*с;
ν - кинематический коэффициент вязкости, м2/с.