Устойчивость САУ

Устойчивость САУ
Устойчивостью называют свойство САУ возвращаться к последующему установившемуся состоянию после приложения возмущающего воздействия, которое вывело её из состояния равновесия.
Системы АУ, обладающие указанным свойством, называют устойчивыми. Системы, в которых не восстанавливается равновесный режим, а при отклонениях от него регулируемая величина начинает неограниченно возрастать или совершать колебания с возрастающей амплитудой, называют неустойчивыми.
Обеспечение устойчивости является необходимым условием работоспособности.
Поэтому исследование САУ на устойчивость представляет собой одну из основных задач в ТН.
Различают два вида устойчивости: устойчивость в «малом» и устойчивость в «большом».

САУ называют устойчивой в «малом», если устойчивость проявляется в результате бесконечно малых изменений возмущающего воздействия. В том случае, когда система сохраняет устойчивое состояние при достаточно больших, конечных по величине изменениях возмущающего воздействия, то САУ называют устойчивой в «большом».
Для линейных систем регулирования требования устойчивости в «малом» является необходимым и достаточным условием устойчивости в «большом». Для нелинейной системы устойчивость в «малом» в общем случае не означает, что она устойчива в «большом».

Причиной неустойчивости замкнутых САУ является наличие в них элементов, способных запасать энергию. В электрических цепях такими аккумуляторами являются индуктивности и ёмкости. В механических системах ту же роль играют движущиеся массы, обладающие механической инерцией.
В электромеханических системах, системах электропривода такими накопителями энергии являются как индуктивности и ёмкости, так и движущиеся массы.
В замкнутых САУ часть энергии с выхода передаётся на вход системы. Если бы передача энергии совершалась без задержки времени, что реально невыполнимо, то, по-видимому, проблемы обеспечения устойчивости не было бы. Применение безынерционных аппаратов – вентильных преобразователей, полупроводниковых и вентильных усилителей и так далее способствует инерционности САУ электропривода.

5.1 Устойчивость звена
Линейное звено является устойчивым, если после окончания внешнего воздействия его состояние с течением времени возвратится к исходному.
звено неустойчиво, если
звено нейтрально, если
звено устойчиво, если

Комплексной паре корней характеристического уравнения
соответствует слагаемое вида

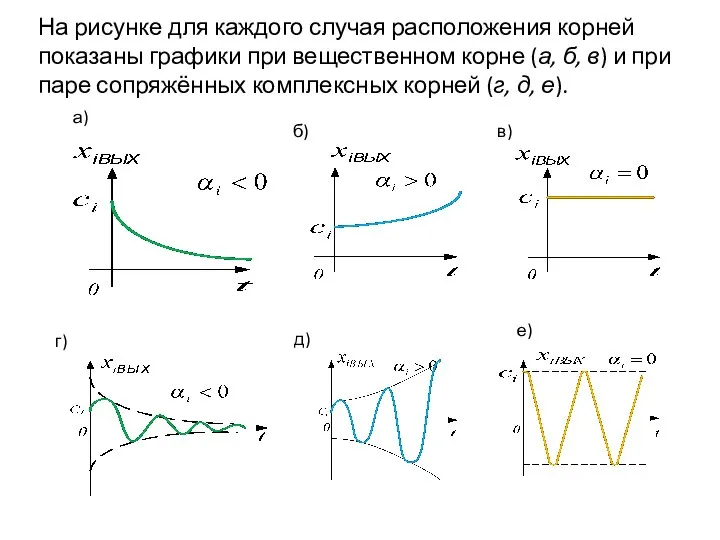
На рисунке для каждого случая расположения корней показаны графики при вещественном корне (а, б, в) и при паре сопряжённых комплексных корней (г, д, е).
а)
б)
в)
г)
д)
е)

5.2 Критерии устойчивости
Критерии устойчивости – это правило, позволяющее без непосредственного определения корней характеристического уравнения САУ определять их расположение на комплексной плоскости корней.
Такая задача впервые была поставлена Максвеллом в 1868 г. и решена Гауссом в 1873 году. Позднее, в 1895 году по просьбе словацкого профессора Стодолы, занимающегося исследованием процесса регулирования турбины, швейцарским математиком Гурвицем был найден алгебраический критерий устойчивости, который формулирует условия устойчивости в форме определителей (в матричной форме). Несмотря на то, что критерии Гаусса и Гурвица одинаковы по содержанию и отличаются лишь по форме, критерий Гурвица нашёл более широкое применение.
Различают два вида критериев:
Алгебраические критерии (Гаусса, Гурвица).
Частотные критерии (Михайлова, Найквиста).

5. 3 Алгебраический критерий устойчивости Гурвица
Пусть дано характеристическое уравнение
Теорема Гурвица гласит: все корни уравнения будут иметь отрицательные действительные части тогда и только тогда, когда все диагональные определители главного определителя положительны.

Рассмотрим примеры.
Пример 5.1. Установить, устойчива ли система, если характеристическое уравнение её имеет вид:
a)
б)
- система не устойчива, так как не выполнено достаточное условие.

a)
б)Вычисляем диагональные определители
итак, система устойчива при
.

Существенные недостатки критерия Гурвица:
Критерий лишен наглядности, носит формальный характер и ничего не говорит о качестве устойчивости, то есть насколько далека система от границы устойчивости.
Коэффициенты или параметры, характеризующие физические свойства звеньев системы, входят зачастую в столь сложных комбинациях, что практически трудно установить, какие именно параметры и каких звеньев следует изменить, чтобы обеспечить устойчивость САР.
Необходимо иметь аналитические уравнения звеньев и всей системы, что не всегда удобно.

5.1 Частотные критерии устойчивости
Впервые были использованы частотные методы определения устойчивости Найквистом при исследовании электронных усилителей с отрицательной обратной связью. Для САУ впервые обосновал и обобщил частотные методы в 1938 году А.В.Михайлов (статья «Метод гармонического баланса в теории регулирования», «Автоматика и телемеханика» №3, 1938 год).
Пусть дано характеристическое уравнение
Если заменить в , то получится характеристический вектор

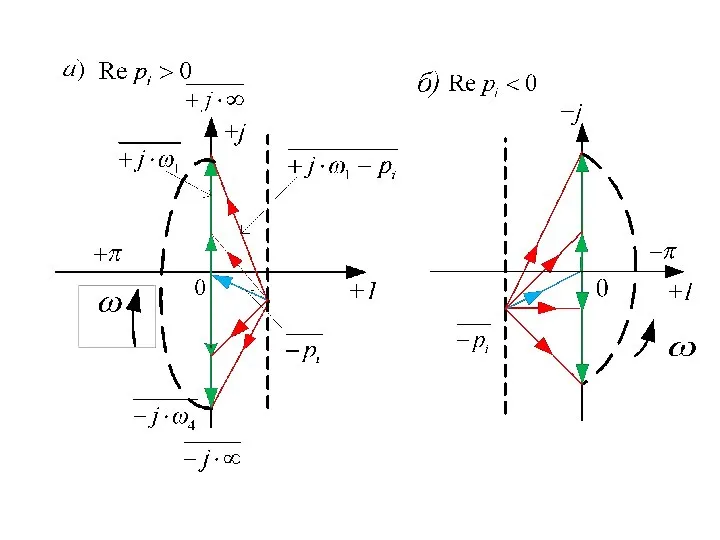
В основе критерия Михайлова лежит известный в теории функций комплексного переменного принцип аргумента.
Характеристический вектор может быть разложен на множители по теореме Виетта
Найдём аргумент комплексного числа
Изменение аргумента вектора
при изменении

Согласно (5.17) для определения изменения аргумента необходимо подсчитать сумму изменений аргументов двучленов при изменении
, то каждый вектор повернётся
на угол «б)»

:
Для устойчивой системы при изменении
(1)

5.2 Частотный критерий устойчивости Михайлова
.

На комплексной плоскости он может быть представлен в виде вектора.

Словами его можно выразить так:

Пример 1
Определить устойчивость системы, характеристическое уравнение которой

Решение:

Составим таблицу:

Пример 2
Определить устойчивость системы, характеристическое уравнение которой

Решение:

Составим таблицу:
2

Пример 3
Определить устойчивость системы, характеристическое уравнение которой

Решение:

Составим таблицу:
1

5.5 Частотный критерий устойчивости Найквиста
Для исследования устойчивости усилителей с обратной связью Найквист в 1932 г. предложил критерий устойчивости, основанный на анализе частотных характеристик системы. Для исследования устойчивости замкнутой системы управления, согласно этому критерию, необходимо знать амплитудно-фазовую частотную характеристику разомкнутой системы, которую можно получить аналитически, так и экспериментально. Последнее обстоятельство выгодно отличает рассматриваемый критерий устойчивости.

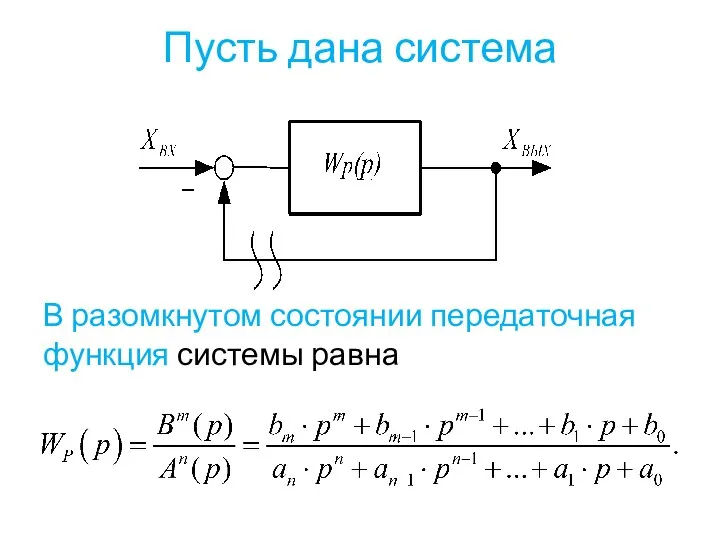
Пусть дана система
В разомкнутом состоянии передаточная функция системы равна

Передаточная функция замкнутой системы равна
Так как , то порядок полинома
и полинома одинаков.
Рассмотрим отдельно знаменатель
где - характеристическое уравнение разомкнутой системы;
- характеристическое уравнение замкнутой системы.
Т.е. характеристические уравнения разомкнутой и замкнутой систем связаны общим уравнением.

Для получения АФЧХ системы положим
где - АФЧХ замкнутой САУ,
- АФЧХ разомкнутой САУ.
Рассмотрим три случая состояния разомкнутой системы: устойчива, неустойчива и находится на грани устойчивости.

1 случай - рассмотрим случай, когда разомкнутая система устойчива.
Если САУ в разомкнутом состоянии устойчива, то по критерию Михайлова
Если потребовать, чтобы система в замкнутом состоянии была устойчива, то должно удовлетворяться равенство
При этом из следует, что

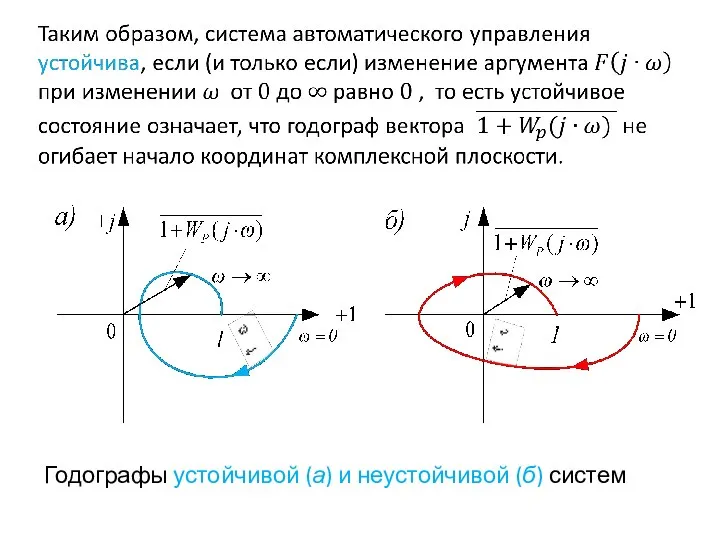
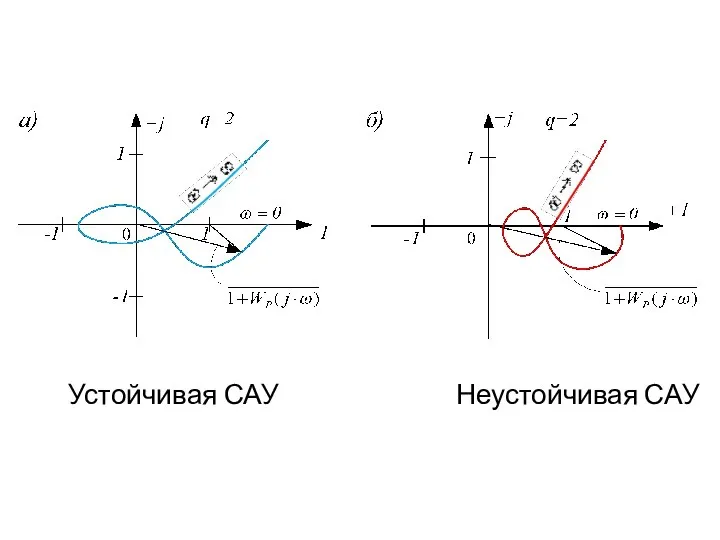
Годографы устойчивой (а) и неустойчивой (б) систем

Устойчивая САУ Неустойчивая САУ

Формулировка критерия Найквиста

Для устойчивой замкнутой системы по-прежнему выполняется равенство

Таким образом, приращение аргумента равно

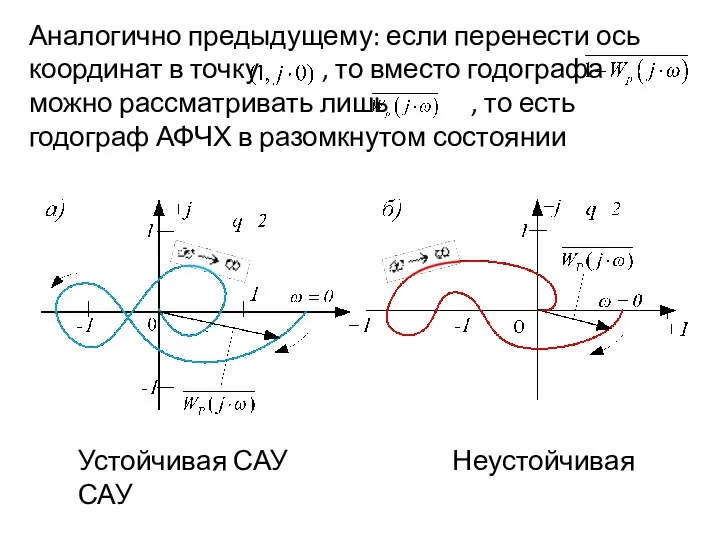
Устойчивая САУ Неустойчивая САУ

Аналогично предыдущему: если перенести ось координат в точку , то вместо годографа
можно рассматривать лишь , то есть годограф АФЧХ в разомкнутом состоянии
Устойчивая САУ Неустойчивая САУ

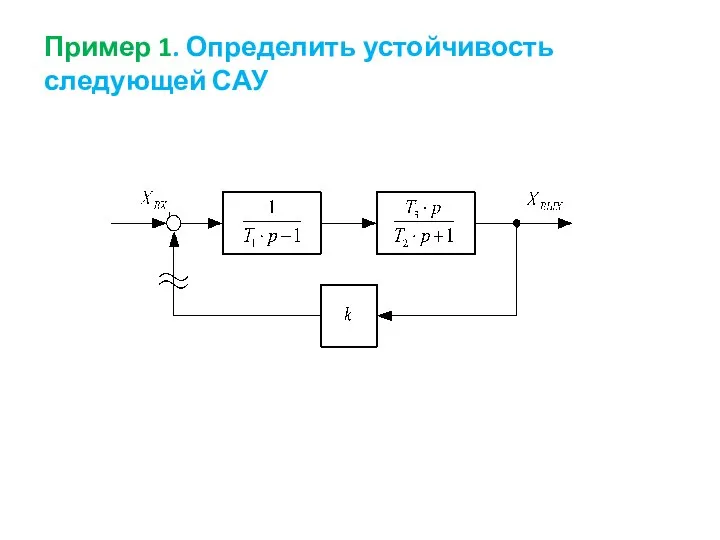
Пример 1. Определить устойчивость следующей САУ

Решение:
Реально такой структурной схеме может соответствовать система Г-Д (генератор-двигатель) с отрицательной обратной связью по току.
Передаточная функция разомкнутой САУ равна

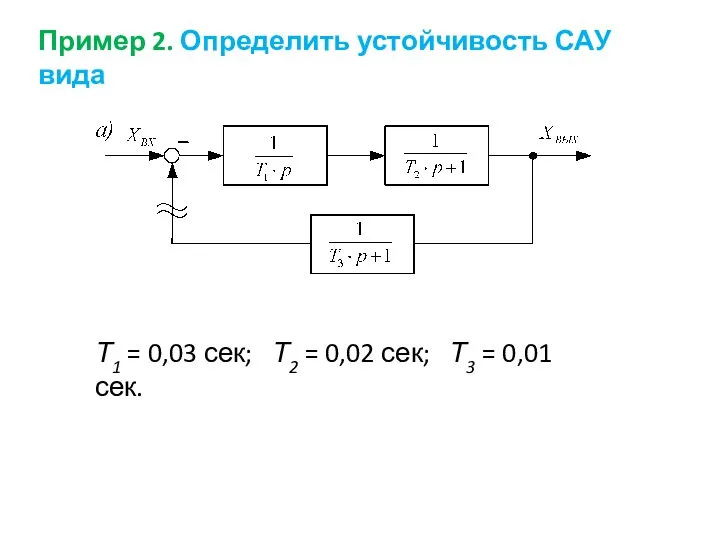
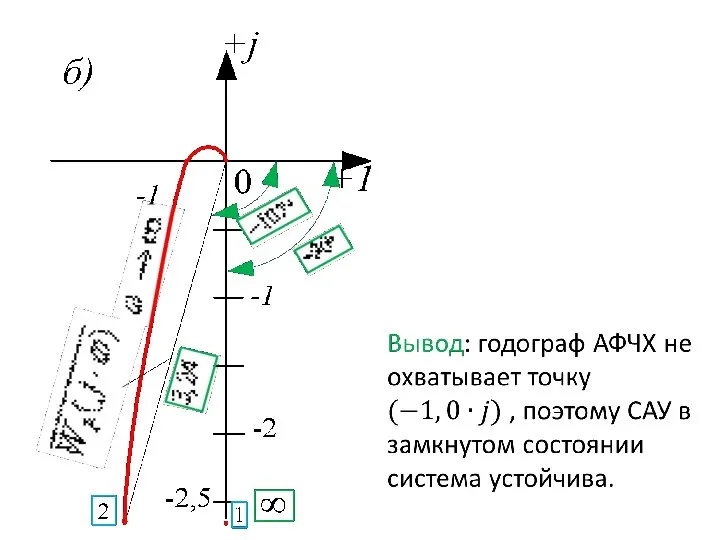
Пример 2. Определить устойчивость САУ вида
Т1 = 0,03 сек; Т2 = 0,02 сек; Т3 = 0,01 сек.

Так как система имеет интегральное звено, то она относится к разряду астатических САУ.
Передаточная функция разомкнутой системы

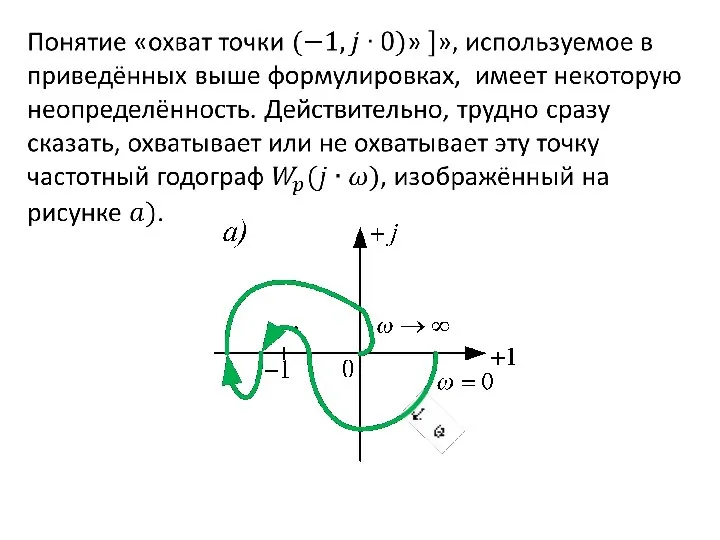
Обобщенный критерий Найквиста (случаи 1-3). Правило перехода

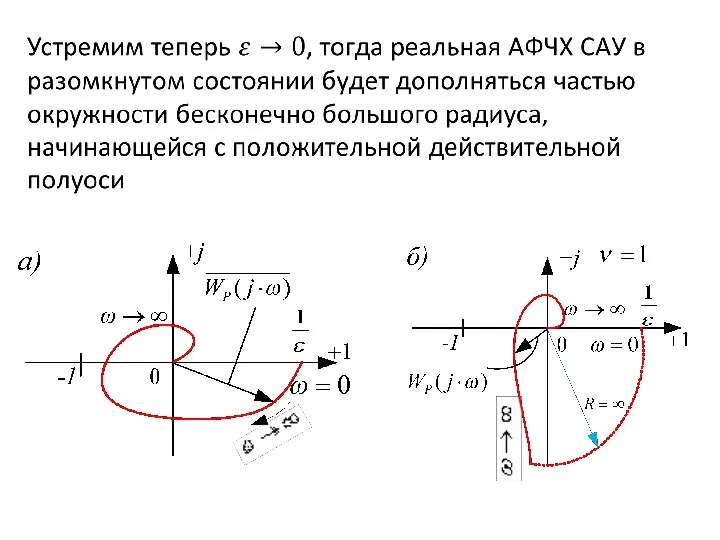
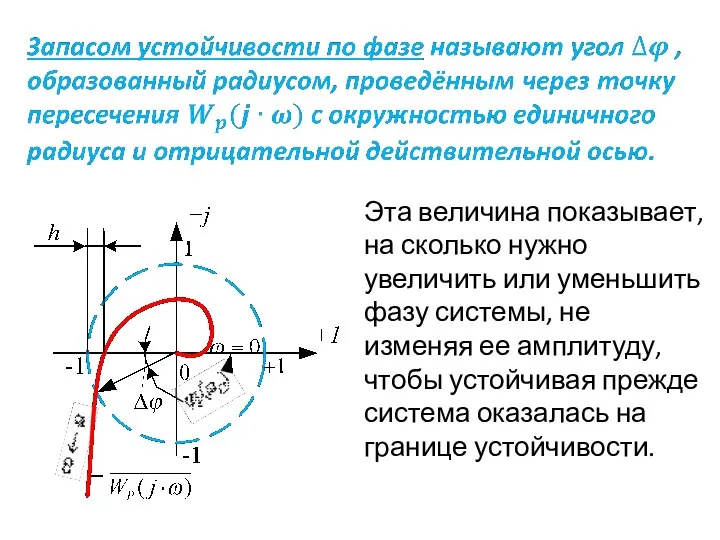
Эта величина показывает, на сколько нужно увеличить или уменьшить фазу системы, не изменяя ее амплитуду, чтобы устойчивая прежде система оказалась на границе устойчивости.

Суждение об устойчивости на основании критерия Найквиста по логарифмическим частотным характеристикам системы в разомкнутом состоянии
Критерий Найквиста можно использовать и по отношению к логарифмическим частотным характеристикам. Согласно критерию устойчивости Найквиста САУ устойчива, если при
Если использовать логарифмический масштаб, то это означает, что

Если логарифмическая фазо-частотная характеристика системы в разомкнутом состоянии при частоте среза (то есть при частоте, где логарифмическая амплитудно-частотная характеристика пересекает ось абсцисс) не достигает значения -180 град, то система в замкнутом состоянии устойчива.
САУ устойчива САУ на грани устойчивости САУ неустойчива

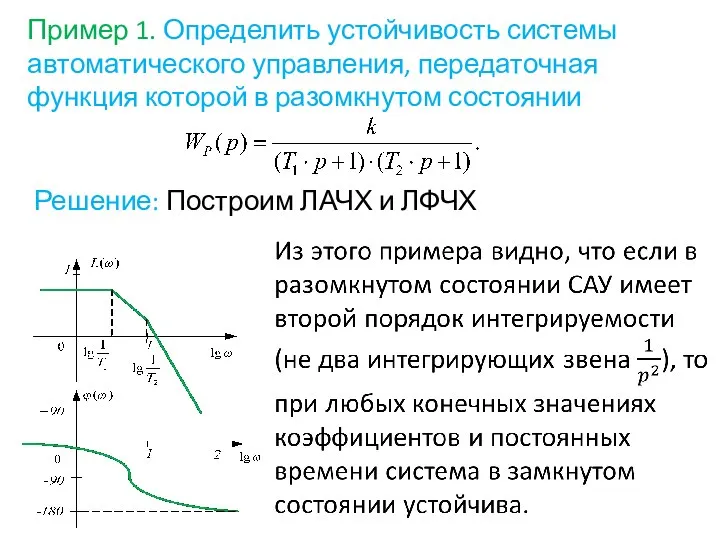
Пример 1. Определить устойчивость системы автоматического управления, передаточная функция которой в разомкнутом состоянии
Решение: Построим ЛАЧХ и ЛФЧХ

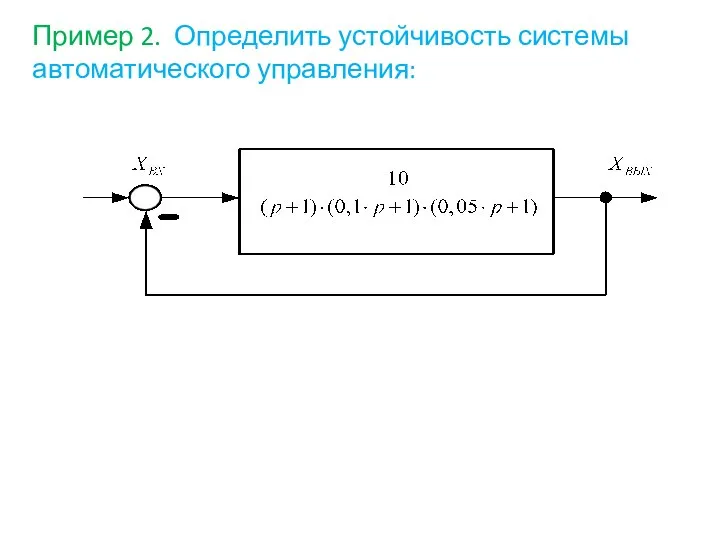
Пример 2. Определить устойчивость системы автоматического управления:

Решение:
Передаточная функция разомкнутой системы равна
Найдём величины, необходимые для построения логарифмических амплитудно-фазовых характеристик

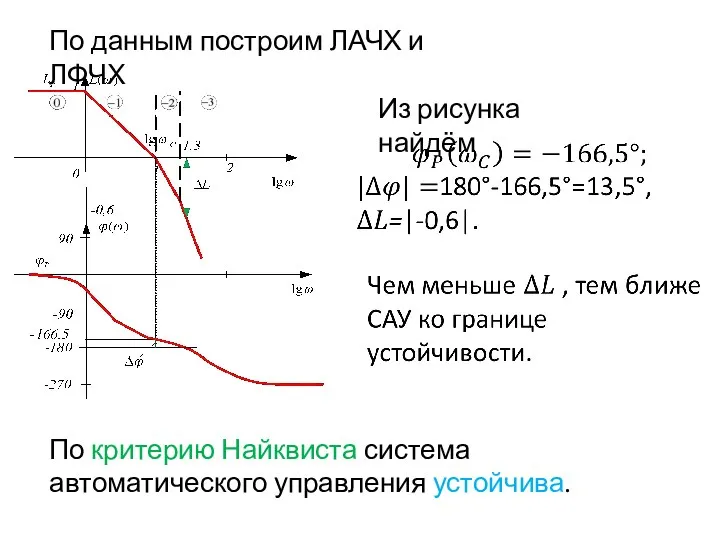
По данным построим ЛАЧХ и ЛФЧХ
Из рисунка найдём
По критерию Найквиста система автоматического управления устойчива.

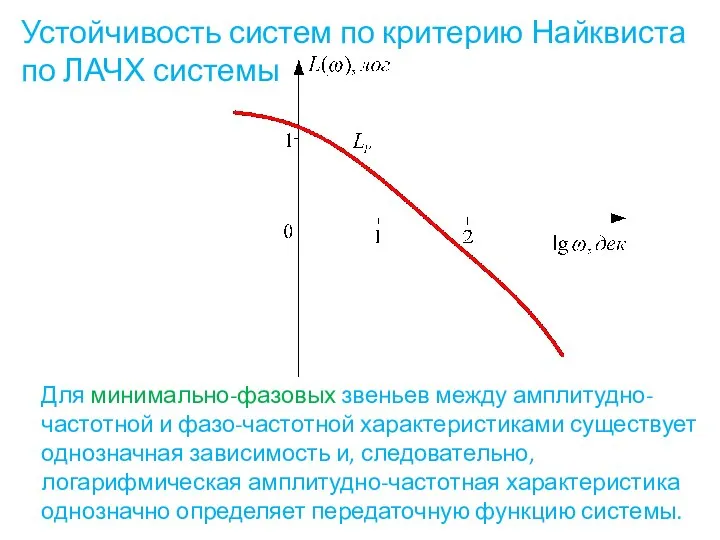
Устойчивость систем по критерию Найквиста по ЛАЧХ системы
Для минимально-фазовых звеньев между амплитудно-частотной и фазо-частотной характеристиками существует однозначная зависимость и, следовательно, логарифмическая амплитудно-частотная характеристика однозначно определяет передаточную функцию системы.

Пример 3. Определить устойчивость замкнутой системы, передаточная функция которой в разомкнутом состоянии равна

Решение:
Вычислим параметры, необходимые для построения логарифмической амплитудно-фазовой характеристики

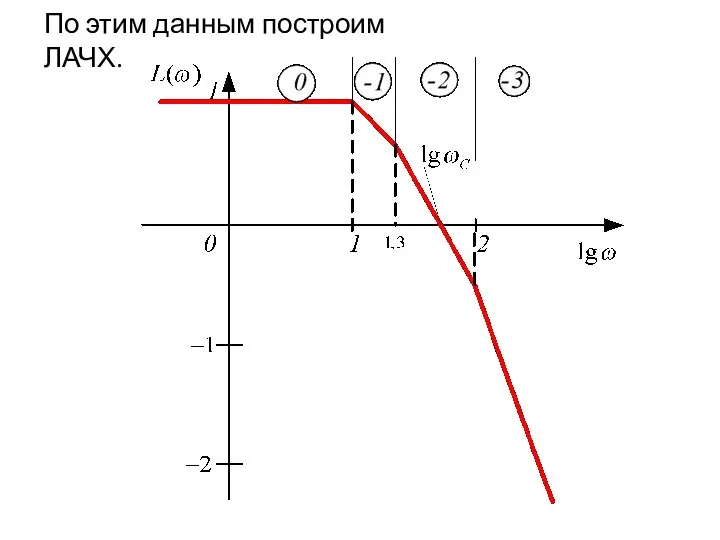
По этим данным построим ЛАЧХ.

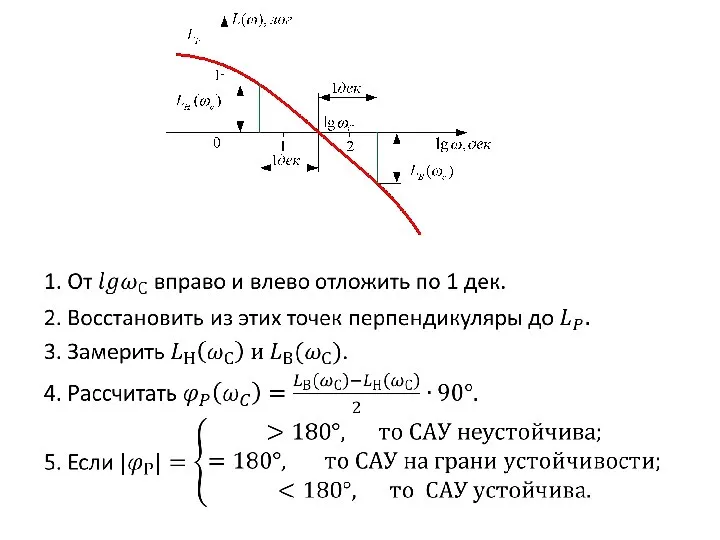
Из геометрических соображений найдём частоту среза системы:
От этой частоты отложим 1дек влево, 1дек вправо. По характеристике вычислим
Вывод: система в замкнутом состоянии устойчива.

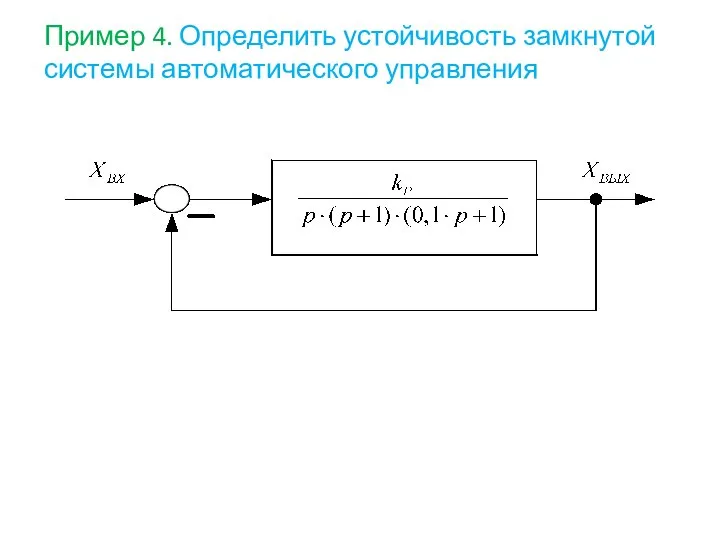
Пример 4. Определить устойчивость замкнутой системы автоматического управления

Решение:
Вычислим параметры, необходимые для построения логарифмических частотных характеристик

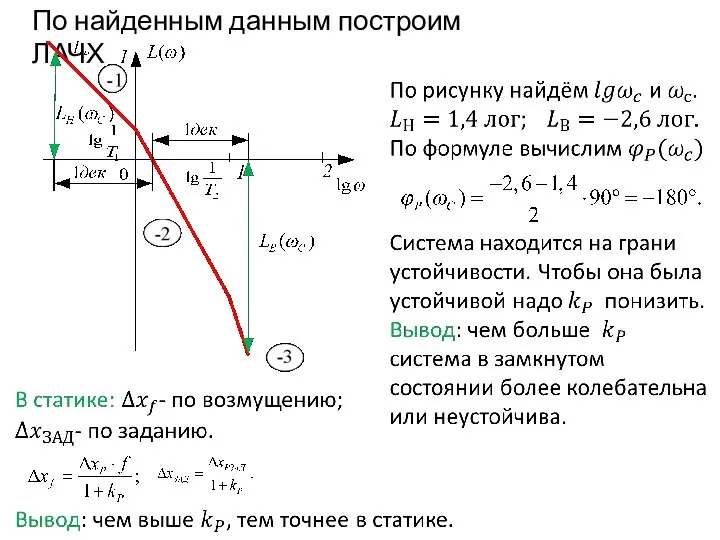
По найденным данным построим ЛАЧХ

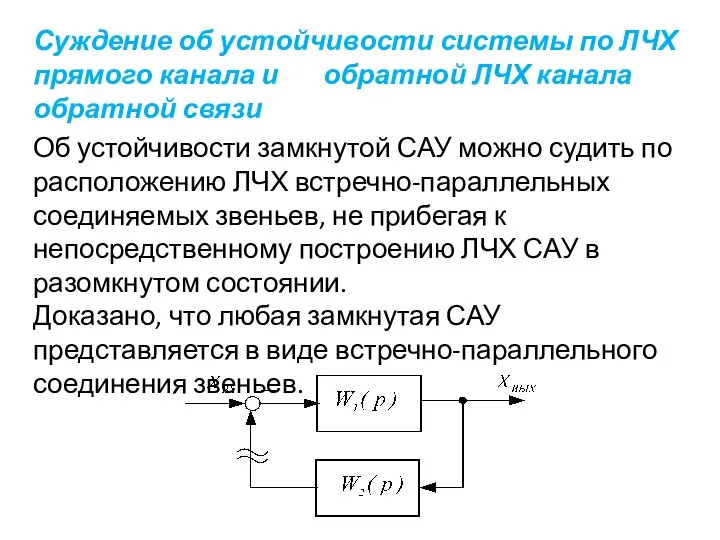
Суждение об устойчивости системы по ЛЧХ прямого канала и обратной ЛЧХ канала обратной связи
Об устойчивости замкнутой САУ можно судить по расположению ЛЧХ встречно-параллельных соединяемых звеньев, не прибегая к непосредственному построению ЛЧХ САУ в разомкнутом состоянии.
Доказано, что любая замкнутая САУ представляется в виде встречно-параллельного соединения звеньев.

Передаточная функция разомкнутой системы равна
Комплексный коэффициент передачи
Для построения ЛАЧХ и ЛФЧХ системы автоматического управления необходимо построить характеристики
и определить поправки.
2
2

Как известно
1
1
то есть ординаты между ЛАЧХ и ЛФЧХ прямого и обратного каналов представляют собой значения соответственно ЛАЧХ и ЛФЧХ системы в разомкнутом состоянии.
Пересечения ЛАЧХ прямого и обратного каналов происходят при частоте среза, то есть

Таким образом, применительно к рассмотренному соединению звеньев критерий устойчивости Найквиста может быть сформулирован следующим образом.
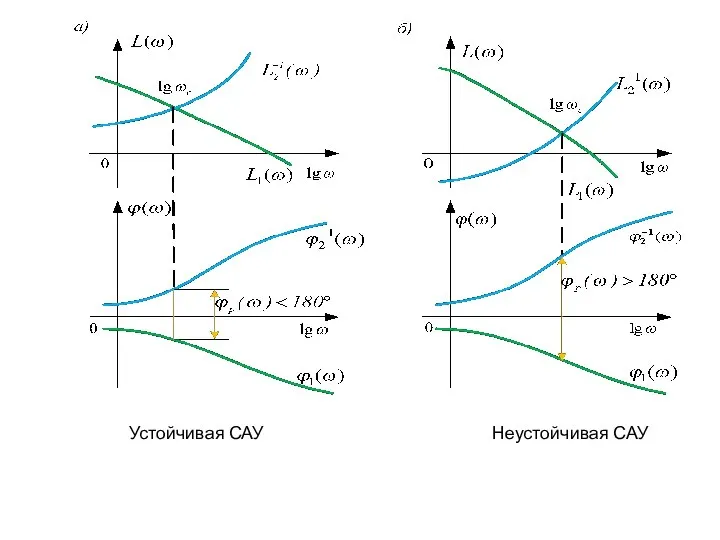
Система автоматического управления в замкнутом состоянии устойчива, если в точке пересечения логарифмических амплитудно-частотных характеристик прямого канала и обратной амплитудно-частотной характеристики канала обратной связи разность фаз между логарифмической фазо-частотной характеристикой прямого канала и обратной логарифмической фазо-частотной характеристикой канала обратной связи меньше 180°.

Устойчивая САУ Неустойчивая САУ

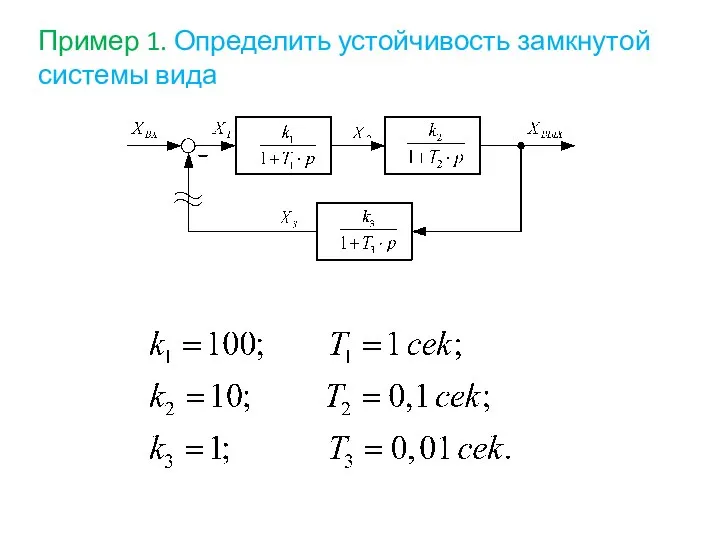
Пример 1. Определить устойчивость замкнутой системы вида

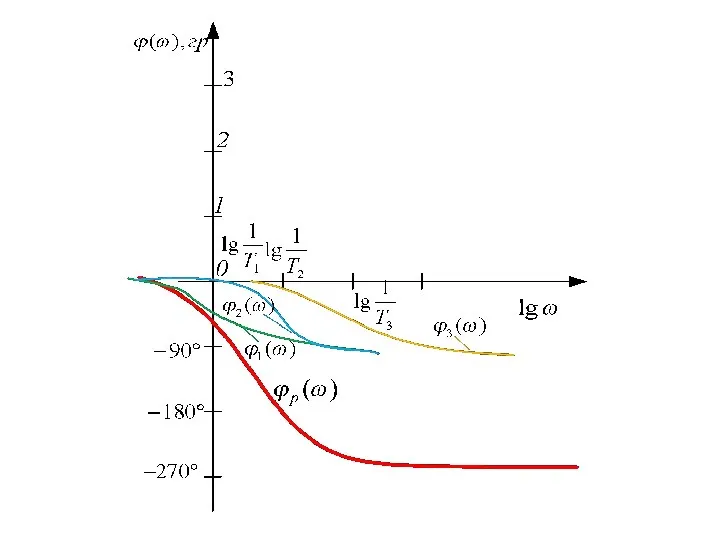
Решение:
Построим ЛАФЧХ системы в разомкнутом состоянии, то есть такой системы:
Определим параметры, необходимые для построения ЛАЧХ и ЛФЧХ

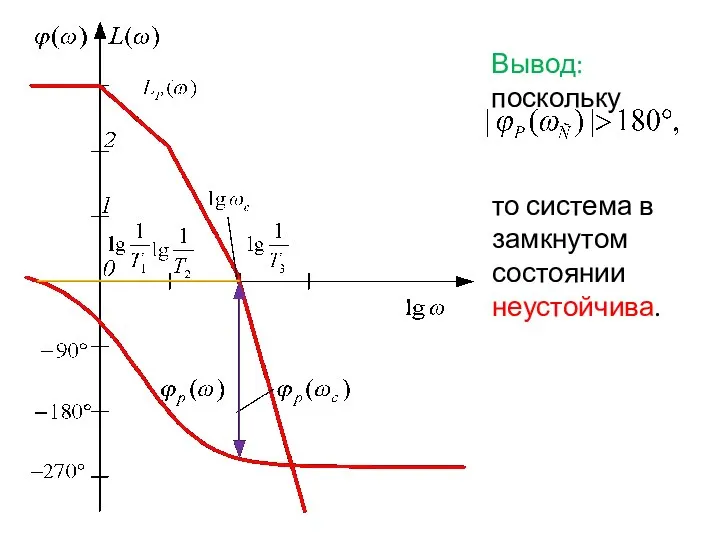
Вывод: поскольку
то система в замкнутом состоянии неустойчива.

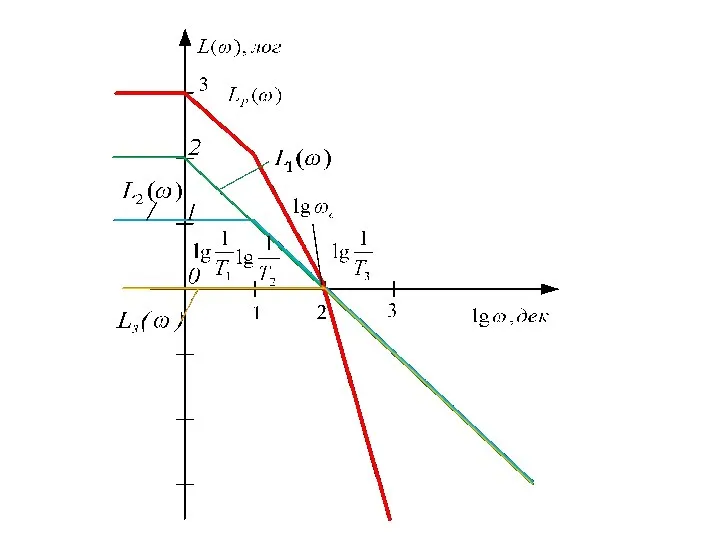
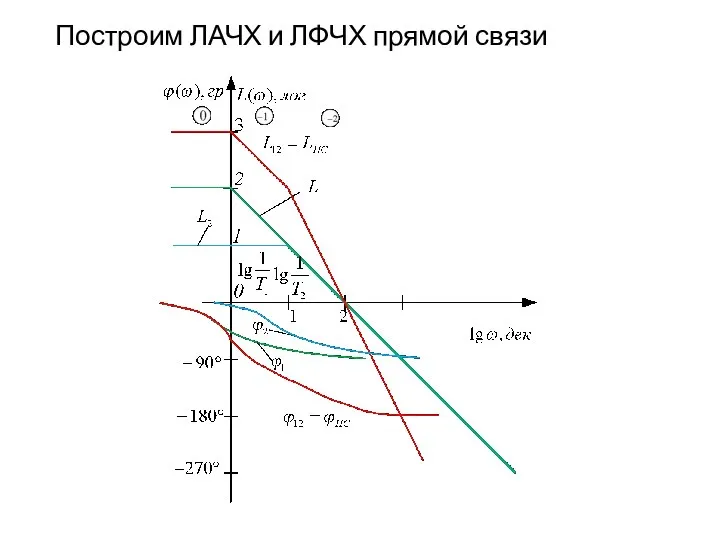
Построим ЛАЧХ и ЛФЧХ прямой связи

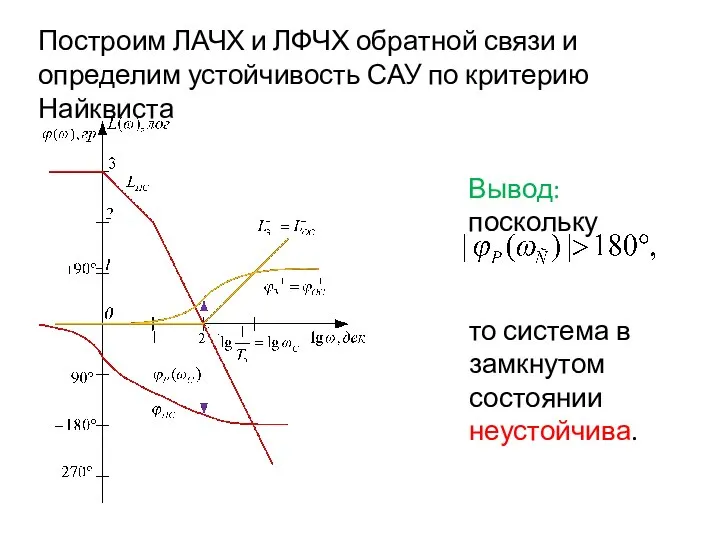
Построим ЛАЧХ и ЛФЧХ обратной связи и определим устойчивость САУ по критерию Найквиста
Вывод: поскольку
то система в замкнутом состоянии неустойчива.