Вырождение влияния критериев

На основе теории подобия можно получить безразмерные величины и вывести условия точного подобия для любых процессов. Однако, в ряде случаев, в частности для процессов, развивающихся под действием нескольких физических эффектов, число безразмерных величин оказывается достаточно большим, а зависимости между ними – сложными. При этом, теория точного подобия не даёт рекомендаций по получению наиболее рациональной системы критериев и упрощению зависимостей между ними. Кроме того, для некоторых сложных процессов, оказывается затруднительно выполнить условия точного подобия, т.е. условия равенства для модели и оригинала сразу нескольких критериев
Для решения этих задач можно воспользоваться следующим широко используемым в науке и технике принципом приближения: если процесс развивается под действием нескольких физических эффектов одинаковой природы, но разной величины, то влияние на процесс эффекта малой по сравнению с остальными величинами должно быть незначительным, и влиянием такого эффекта можно пренебречь. В этом случае говорят о вырождении критериев подобия и проявлении свойства автомодельности. Независимость процесса от каких-либо критериев подобия упрощает построение модели и поэтому желательна.

Математически этот принцип можно выразить следующим образом: если в уравнении, выражающем условие равенства нулю суммы нескольких членов, имеются слагаемые несоизмеримо малые по сравнению с остальными, то этими малыми слагаемыми можно пренебречь.
Бесконечное уменьшение или увеличение численного значения критерия говорит о несоизмеримости сопоставляемых эффектов. Поэтому влияние на процесс бесконечно больших и малых критериев должно вырождаться.
С этой целью проанализируем закономерности процессов, развивающихся под действием трех каких-либо физических эффектов, и особенности описывающих такие процессы безразмерных зависимостей при различных соотношениях между эффектами.

Уравнение математической физики для процессов, развивающихся под действием трёх физических эффектов, в общем случае имеет такой вид:
где - дифференциальные операторы, каждый из которых является математическим выражением соответствующих физических эффектов. При этом один из эффектов (эффект-функция) является результатом действия остальных (эффектов-параметров и эффектов-аргументов). Для определённости будем считать, что в (1) эффектом-функцией является .
Разделим уравнение (1) на один из независимых операторов, для определенности – на первый. При этом оператор, на который делят остальные, а, следовательно, и эффект, с которым сравниваются остальные, будем называть базовым.
(1)

В результате получим:
(2)
Уравнение вида (2) можно преобразовать в зависимости между безразмерными величинами, являющимися приближенной мерой порядка соответствующих относительных операторов:
,
Знак ~ говорит о том, что сравниваемые величины имеют один порядок, т.е. соизмеримы между собой.
В результате преобразования из уравнения (2) получим:
или
(3)

Рассмотрим случаи различных соотношений между эффектами:
1) Случай, когда все эффекты соразмерны между собой:
.
При этом будут иметь место такие соотношения:
Но так как критерии являются приближенной мерой соотношения эффектов, то и численные значения соответствующих критериев тоже должны быть соизмеримы с единицей:
,
Так как влияние на процесс соизмеримых эффектов должно быть существенным, существенным должна быть и зависимость между критериями, соизмеримыми с единицей.
2) Случай, когда 1 из действующих независимых эффектов несоизмеримо мал по сравнению с остальными. Предположим, что мал второй эффект:
.
Тогда получим такие соотношения:
или

Если какой-то из действующих эффектов становится малым по сравнению с другими, то безразмерный комплекс, числителем которого стоит такой эффект, становится малым по сравнению с единицей.
Так как влияние эффекта является сравнительно малым по сравнению с другими эффектами, а, следовательно, то таким критерием (и эффектом) можно пренебречь.
В результате уравнение (1) приобретает вид:
(4)
Такое уравнение соответствует случаю, когда существенными для процесса являются только два физических эффекта, причём один можно рассматривать как результат действия второго.
В этом случае обязательно выполняется условие:
(5)
Следовательно, если для процесса существенны только два эффекта, один из которых является результатом действия другого, то численные значения их должны быть равны.

Из уравнения (4) можно получить лишь один безразмерный комплекс
и этот комплекс должен быть равен постоянной величине
Причём, численное значение такого комплекса должно быть соизмеримо с единицей, т.е. иметь порядок единицы
Т.о., при бесконечном уменьшении численного значения критерия
влияние такого критерия в приведенной системе вырождается.
3) Случай, когда малым по сравнению с остальными становится другой эффект, а именно . Очевидно, что влиянием на процесс такого эффекта в этом случае можно пренебречь. Однако, при преобразовании, аналогичном предыдущему случаю, получим такие соотношения:
Зависимость (3) в этом случае становится неопределённой, т.к. входящие в неё величины стремятся к бесконечности. Для получения рациональной безразмерной зависимости сопоставлять эффекты нужно не с самым малым, а с одним из существенных. Так как результат действия остальных независимых эффектов за базовый эффект примем независимый

Тогда уравнение (1) примет вид:
(6)
Отсюда вытекает:
или
Влиянием критерия так же можно пренебречь, в результате чего получим постоянство значения нового критерия
Следовательно, при новой форме критериев опять получается вырождение безразмерной зависимости и влияния одного из критериев.
Сравним полученный новый критерий со старым. Легко доказать, что:
Поэтому, если выразим безразмерную зависимость в исходных комплексах, то получим при

На практике нередко используются критерии с различными степенями одних и тех же физических величин. С физической точки зрения такие критерии представляют преобразование вида:
где – показатель степени, обычно имеющий такие показатели как:
Если безразмерная зависимость может иметь более общий вид:
Таким образом, при рассмотренных вариантах преобразования безразмерная зависимость между двумя критериями вырождается в зависимость , что отражает постоянство исходной безразмерной функции в одном из крайних случаев, например, при

И в зависимость отражающую постоянство другой безразмерной функции в крайнем случае, например, при
причем, в этом крайнем случае так же оказывается постоянным значение безразмерной функции, но не исходной, а той которая получена путём объединения исходных критериев.
Практически это означает, что влияние любого критерия в одной из предельных областей становится несущественным, а в противоположной предельной области влияние такого критерия становится несамостоятельным.

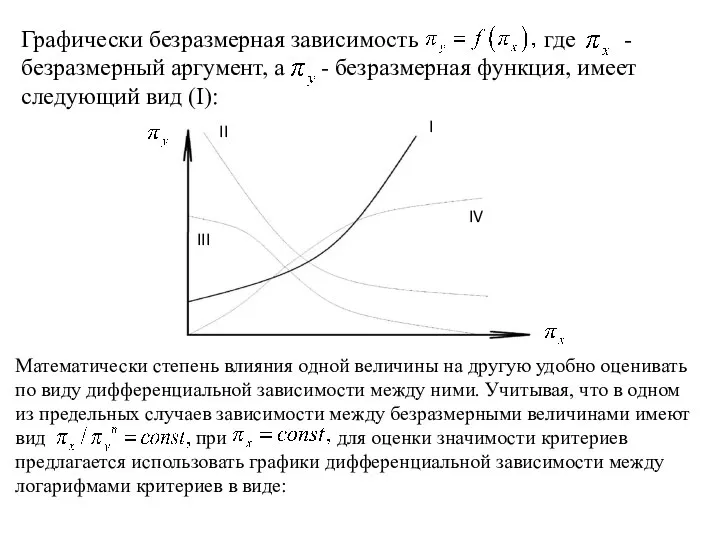
Графически безразмерная зависимость где - безразмерный аргумент, а - безразмерная функция, имеет следующий вид (I):
Математически степень влияния одной величины на другую удобно оценивать по виду дифференциальной зависимости между ними. Учитывая, что в одном из предельных случаев зависимости между безразмерными величинами имеют вид при для оценки значимости критериев предлагается использовать графики дифференциальной зависимости между логарифмами критериев в виде:
I
II
III
IV

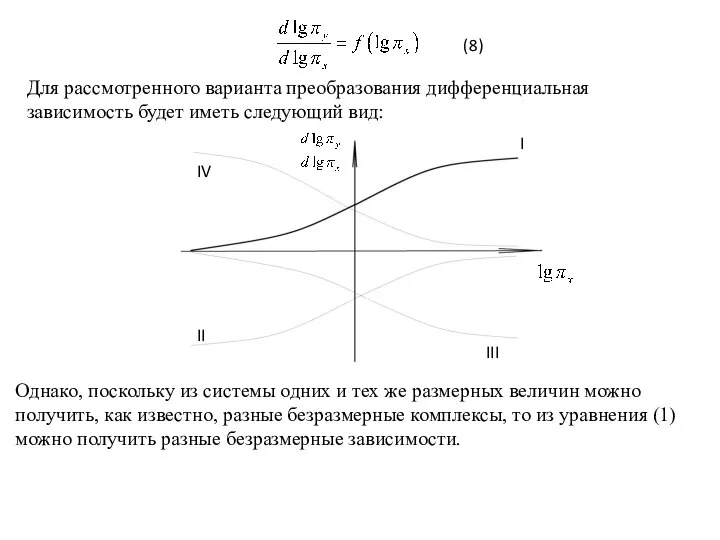
(8)
Для рассмотренного варианта преобразования дифференциальная зависимость будет иметь следующий вид:
Однако, поскольку из системы одних и тех же размерных величин можно получить, как известно, разные безразмерные комплексы, то из уравнения (1) можно получить разные безразмерные зависимости.
I
II
III
IV

В качестве безразмерной функции здесь выступает а в качестве безразмерного аргумента для I - II -
В качестве безразмерной функции здесь выступает а в качестве безразмерного аргумента для III - IV -
Из приведённых данных видно, что зависимости между двумя безразмерными величинами в широком диапазоне изменения численных значений критерия от 0 до имеют 3 различные области.

Область существенного влияния критерия, соответствующая переменному значению производной
Численные значения критерия в этой области соизмеримы с единицей
2. Область несущественного влияния критерия, соответствующая
равенству нулю или пренебрежимо малому значению
производной
Следовательно
Численные значения независимого критерия при этом находятся в одной из предельных областей: либо либо
и

Область несамостоятельного или формального влияния критерия, соответствующая практически постоянному значению производной
следовательно
Численные значения независимого критерия при этом находятся в противоположной от «Случая 2» области.
при
Аналогичные закономерности присущи и зависимостям между большим числом безразмерных величин. В этих случаях получим, что при несоизмеримости с единицей нескольких критериев безразмерная зависимость так же сводится к постоянству критериев – функций.

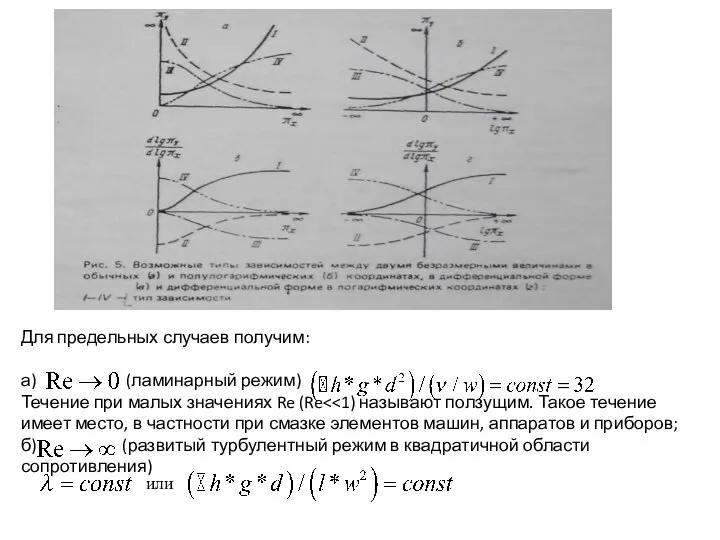
Пример безразмерной зависимости из области аэродинамики и теплообмена:
Потери напора при длине трубы при движении несжимаемой жидкости.
Согласно формуле Дарси – Вейсбаха:
где -безразмерный коэффициент трения.
На рисунке 1а показаны полученные Л. Никурадзе и Г.А. Муриным данные для зависимости . В дифференциальной форме эти данные можно представить в виде, показанном на рис.1б.
Видно что зависимость совпадает по виду с зависимостью типа II.
Рис 1.

Для предельных случаев получим:
а) (ламинарный режим)
Течение при малых значениях Re (Re<<1) называют ползущим. Такое течение имеет место, в частности при смазке элементов машин, аппаратов и приборов;
б) (развитый турбулентный режим в квадратичной области сопротивления)
или

С учётом выявленных областей безразмерных зависимостей все критерии по значимости для процесса целесообразно подразделять на такие группы:
Существенные;
Вырожденные несущественные;
Вырожденные формальные (несамостоятельные).
Существенными следует считать такие критерии, которые отражают соотношение между соизмеримыми физическими эффектами, а изменение численного значения которых при неизменности любых других существенно влияет на значение безмерной функции.
Признаком существенности критерия является соизмеримость его с единицей. При физическом моделировании выполнение равенства численных значений существенных критериев для модели и образца является обязательным.
Вырожденными следует считать критерии, отражающие соотношения между несоизмеримыми эффектами.
Признаком вырожденности является несоизмеримость критерия с единицей.

Любой критерий при обоих предельных значениях ( и ) вырождается. Однако влияние и роль вырожденных критериев в противоположных предельных областях различны. Если изменение численного значения вырожденного критерия при неизменности остальных критериев данной системы практически не влияет на изменение безразмерной функции, то этот критерий в рассматриваемой системе является несущественным.
Внешние признаки несоизмеримости: а) несоизмеримость с единицей конкретного критерия, в который входит несоизмеримо малый по сравнению с остальными физический эффект; б) соизмеримость с единицей остальных критериев системы.
Если соизмеримо малый по сравнению с остальными (вырожденный) физический эффект входит не в один, а сразу в несколько критериев, то его изменение приводит к изменению значений сразу нескольких критерий. Поэтому хотя вырожденный эффект фактически не может влиять на процесс, формально можно получить зависимость безразмерной функции от больших или малых критериев, как в областях

В связи с этим такие большие или малые критерии, изменение численных значений которых при неизменности остальных в исходной форме приводит к стабильному изменению значения безразмерной функции, следует считать несамостоятельными, или формальными.
Признаком несамостоятельности, т.е. формальности критериев в рассматриваемой совокупности, является несоизмеримость с единицей не одного, а сразу двух или более критериев, имеющих общую группу физических величин. Причем, формальными следует считать все такие несоизмеримые с единицей величины.