Ядерные реакции. Процесс столкновения микрочастицы с атомным ядром

Первая искусственная ядерная реакция
(Э. Резерфорд, 1919 г.)
Снаряды: альфа-частицы, испускаемые естественным радиоактивным препаратом. Результат: появление протонов.
Первая ядерная реакция, осуществленная с помощью ускорителя протонов (1932 г.)
1H1 + 3Li7 → 2He4 + 2He4
2He4 + 7N14 → 8O17 + 1H1
Вековая мечта алхимиков – трансмутация элементов

Примеры ядерных реакций (в краткой записи)
p + 8O17 → 9F17 + n
γ + 20Ca40 → 19K38 + n + p
π− + p → n + π0

Запись ядерной реакции в общем виде:
a + A → B + b + … (3.1)
a – частица-снаряд, A – ядро-мишень, B – дочернее ядро, b,… – образовавшиеся частицы.

В ядерных реакциях сохраняется энергия, равная сумме кинетической энергии и энергии покоя.
Энергетическое уравнение ядерной реакции можно записать в виде:
Ea + EA = EB + Eb + … − Q (3.2)
где
Q = (ma + mA – mb – mB – …) c2 (3.3)
E – кинетические энергии, m – массы частиц,
Q – энергия реакции.
Энергию реакции вводят в запись реакции
a + A → B + b + Q (3.4)
Сохранение энергии

Если сумма масс исходных частиц больше суммы масс частиц-продуктов, то часть энергии покоя, равная Q , перейдет в кинетическую энергию.
При этом энергия реакции Q положительна. Такие реакции называются экзоэнергетическими.
Пример: 1H2 + 1H3 → 2He4 + 0n1 + 17,6 МэВ
(Реакция, идущая в термоядерной бомбе)

Если сумма масс исходных частиц меньше суммы масс частиц-продуктов, то часть кинетической энергии, равная Q , перейдет в энергию покоя.
При этом энергия реакции Q отрицательна. Такие реакции называются эндоэнергетическими.
Примеры: 2He4 + 2He4 → 1H1 + 3Li7 - 17 МэВ
5B11 + 1H1 → 0n1 + 6C11 – 2,76 МэВ

Упругое рассеяние
a + A → a + A (3.5)
Энергия такой реакции равна нулю.
Пример: p + 3Li7 → p + 3Li7
В этих реакциях происходит перераспределение энергии и импульса между частицами а и А.

Экзоэнергетические реакции и упругое рассеяние могут идти при сколь угодно малой кинетической энергии частиц-снарядов.
Эндоэнергетические реакции характеризуются порогом.
Порог эндоэнергетической реакции – это минимальная энергия исходных частиц, при которой возможна реакция.
В реакции сохраняется не только энергия, но импульс системы частиц. Как следствие, в лабораторной системе порог Eпор не совпадает с абсолютной величиной энергии реакции ⎮Q⎮.

Рассмотрим нерелятивистский процесс.
В лабораторной системе отсчета частица-мишень неподвижна, т.е. pA = 0.
Порог эндоэнергетической реакции
Центр инерции системы «снаряд+мишень» имеет кинетическую энергию:
(3.6)
С другой стороны, связь энергии и импульса снаряда:
(3.7)

Приравнивая правые части уравнений (3.6) и (3.7), получим :
(3.8)
Порог всегда больше абсолютной величиной энергии реакции
Невозможно всю кинетическую энергию снаряда превратить в энергию реакции.
Тогда бы обе частицы остановились, что противоречит сохранению импульса системы снаряд-мишень.

Сохранение момента импульса системы «снаряд+мишень»
Наибольшую вероятность имеют реакции, для которых выполняется неравенство:
(3.9)
где l – орбитальное число системы «снаряд+мишень» , R – радиус действия взаимодействия частиц, λD – дебройлевская длина частицы-снаряда.
Вероятность реакции резко падает с ростом орбитального числа l.

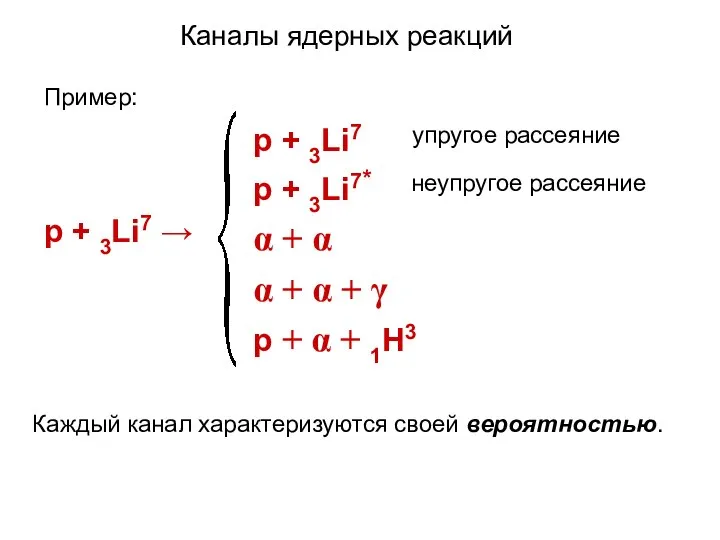
Каналы ядерных реакций
Пример:
Каждый канал характеризуются своей вероятностью.

Дифференциальное эффективное сечение
Характеристика неоднородности углового распределения рассеянных частиц.
Величина dσ интерпретируется как площадка в пространстве, которую пересекают частицы, рассеянные в телесный угол dΩ.
Дифференциальное сечение, как правило является функцией угла рассеяния θ.
(3.9)

Интегральное эффективное сечение
Интегрирование дифференциального эффективного сечения по полному телесному углу дает интегральное эффективное сечение
Величина σ интерпретируется как площадка в пространстве, проходя через которую, частицы взаимодействуют.
(3.10)

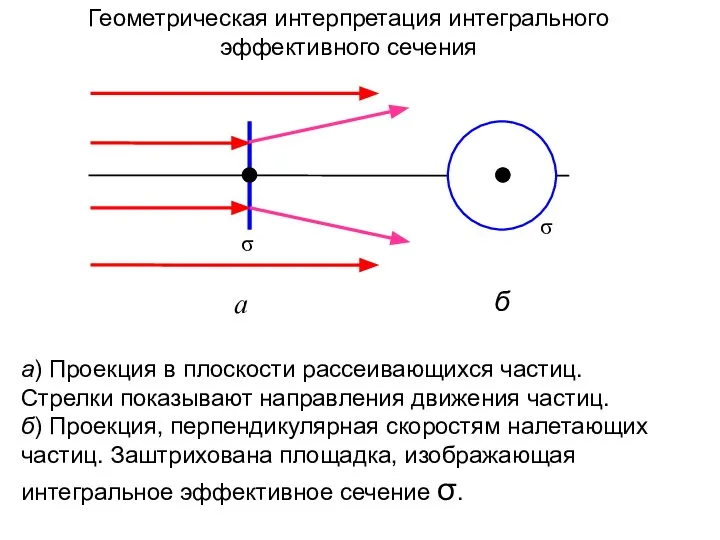
а) Проекция в плоскости рассеивающихся частиц. Стрелки показывают направления движения частиц.
б) Проекция, перпендикулярная скоростям налетающих частиц. Заштрихована площадка, изображающая интегральное эффективное сечение σ.
Геометрическая интерпретация интегрального эффективного сечения

Механизм составного ядра
a + A → C → B + b (3.11)
C – промежуточное составное ядро.
Частица-снаряд попадает в ядро и за характерное ядерное время
τN = RA / va (3.12)
образует составное ядро.
RA – радиус ядра-мишени,
va – скорость частицы-снаряда.
В обычных лабораторных условиях τN ~ 10−22 ÷ 10−21 сек.

Составное ядро получает дополнительную энергию
εa – энергия связи частицы-снаряда в ядре,
Ea – кинетическая энергия частицы-снаряда в лабораторной системе отсчета.
Следовательно, составное ядро всегда образуется в возбуждённом состоянии.
(3.13)

Вследствие сильного взаимодействия нуклонов в ядре энергия возбуждения Е* быстро распределяется почти равномерно между всеми нуклонами, в результате чего каждый из них будет иметь энергию, гораздо меньшую энергии связи нуклона в составном ядре.
В результате статистических процессов энергообмена между нуклонами через некоторое время τ один нуклон (или несколько нуклонов) приобретает энергию, превышающую энергию связи нуклона в составном ядре. Эта частица выходит из ядра как продукт реакции через время τ после образования составном ядре.
Величина τ - случайная
Среднее время τ ~ 10−13 ÷ 10−16 сек ,
(много больше характерного ядерного времени).

Атомное ядро представляет собой систему фермионов, движущиеся в ограниченном пространстве. Такая система обладает дискретным набором стационарных состояний и соответствующих энергий.
При образовании составное ядро находится в определенном стационарном состоянии с энергией Е* из разрешенного дискретного набора.
Переход составного ядра из возбужденного состояния в основное может происходить испусканием гамма-фотона.
При этом характерное время жизни составного ядра составляет τ ~ 10−14 сек.

Шириной энергетического уровня составного ядра , через который идет реакция, называется величина
Г = ħ / τ (3.14)
где τ – время жизни составного ядра
Согласно энергетическому соотношению неопределенности
ΔE⋅ Δt ~ ħ
малое время жизни составного ядра обусловливает значительную ширину энергетического уровня.

где Гb/Г – вероятность распада составного ядра по каналу b.
Г = Гa + Гb + Гb’ + …. (3.16)
Гa , Гb , Гb’ ,… – парциальные ширины.
σaC − сечение образования составного ядра.

Формула Брейта-Вигнера
Пусть некоторый энергетический уровень Е0 составного ядра имеет ширину Г, меньшую чем расстояние между уровнями ΔЕ. Такой уровень называется изолированным.
Для кинетических энергий Е частицы-снаряда близких к Е0 сечение образования составного ядра равно
(3.17)
(3.18)
где

(3.19)
Тогда, согласно (3.15) сечение реакции (3.11)
Формула (3.19) обуславливает резонансный характер зависимости σab(E).
Величина эффективного сечения σab пропорциональна вероятности реакции.

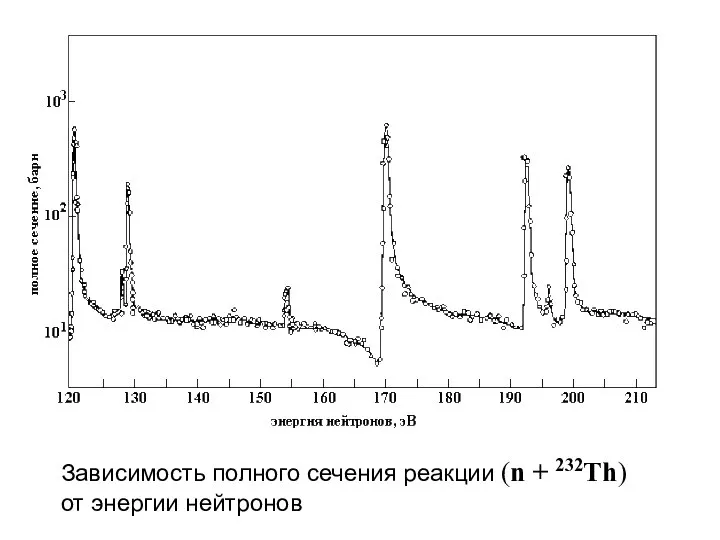
Зависимость полного сечения реакции (n + 232Th) от энергии нейтронов

Нерезонансные реакции
Ширина энергетических уровней Г растет с увеличением энергии Е.
Следовательно, при энергиях более нескольких МэВ сечения реакций не имеют резонансного характера.

Спектр вылетающих из ядра частиц имеет следующий приближенный вид:
(3.21)
где E* - энергия возбуждения составного ядра, εb - энергия связи вылетающей частицы в составном ядре,
С1 и С2 – коэффициенты.

Прямые ядерные реакции
Кроме реакций через составное ядро, происходят прямые ядерные реакции за характерное ядерное время τN ~ 10−22 ÷ 10−21 сек.
В прямых ядерных реакциях энергия частицы-снаряда передается, в основном, одному нуклону.
Прямые ядерные реакции превалируют при высоких энергиях частиц-снарядов (десятки МэВ и более).
В прямых ядерных реакциях частицы вылетают из ядра в направлении, близком к направлению импульса частицы-снаряда.

(n, n); (n, p); (p, n); (p, p); …
Срыв: (d, n); (d, p); …
Подхват: (n, d); (p, d); …
При энергии частиц-снарядов более 100 МэВ происходят реакции квазиупругого выбивания : (p, 2p); (p, pn); …
(n, 1H3); (n, 2He3); (p, α); (n, α); (1H3, α); …
В прямых реакциях могут вылетать ядра лития, бериллия и т.д. Такие ядра называются фрагментами.
Ядро может развалится на несколько частиц.
В прямых реакциях могут возникать новые частицы: пи-мезоны, ка-мезоны, гипероны и др.
Типы прямых ядерных реакций